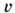частицы жидкости на оси координат представляются в виде частных производныхПотенциальное течение - безвихревое движение жидкости или газа, при к-ром каждый малый объём деформируется и перемещается
поступательно, но не имеет вращения (вихря). При П. т. проекции скорости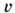
частицы жидкости на оси координат представляются в виде частных производных
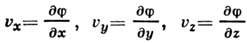
от функции f координат и времени, наз. потенциалом
скорости течения. Движение реальных жидкостей и газов будет потенциальным в
тех областях, в к-рых действие сил вязкости ничтожно мало по сравнению с действием
сил давления (жидкость считается идеальной) и в к-рых нет завихрений, образовавшихся
за счёт срыва со стенок пограничного слоя или за счёт неравномерного нагревания.
Необходимыми и достаточными условиями потенциальности течения являются равенства
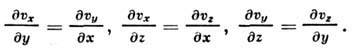
Простейшими примерами П. т. служат поступат.
течение с пост. скоростью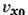 
вдоль
оси x (
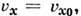
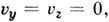потенциал 
''
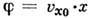+ const), а также источник
и сток в пространстве, для к-рых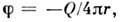 
где Q - постоянная (Q = const) или переменная (Q = Q(t))мощность источника (стока), 
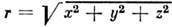- расстояние от начала координат. При Q > 0 жидкость вытекает из начала
координат во всех направлениях (точечный источник), а при Q < 0 -
втекает в начало координат (сток).
Движение идеальной жидкости, возникшее из состояния
покоя, будет потенциальным; будучи потенциальным в к--л. момент времени, оно
будет потенциальным и в последующее время, если давление зависит только от плотности
и массовые силы являются консервативными (см. Консервативная система ).Движение
идеальной несжимаемой (плотность 
=
const) жидкости, вызванное мгновенным приложением импульс-них давлений (внезапное
движение погружённого тела, удар тела о
поверхность жидкости), будет также потенциальным.
Для П. т. дифференц. ур-ния движения идеальной
жидкости приводятся к интегралу Лагранжа - Коши:
где П - потенц. энергия поля массовых сил,
приходящаяся на единицу массы,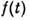 
-
произвольная функция от времени t.
Для установившегося движения соотношение (1)
принимает вид
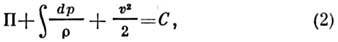
где С - постоянная для всей области П.
т. сжимаемой жидкости. Т. о., для изучения П. т. достаточно определить потенциал
скоростей с помощью неразрывности уравнения, соотношения (2) и ур-ния
физ. состояния. Для несжимаемой жидкости ур-ние неразрывности имеет вид
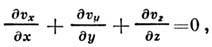
и поэтому изучение П. т. сводится к, решению
ур-ния Лапласа
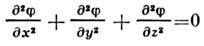
с учётом граничных условий на твёрдых стенках
и на свободной поверхности (условий безотрывности обтекания твёрдых стенок и
условия постоянства давления на свободной поверхности).
Для плоскопараллельного П. т. несжимаемой жидкости
ур-ние неразрывности позволяет ввести функцию тока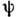
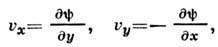
к-рая в комбинации с потенциалом скоростей f
составляет комплексный потенциал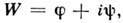 
представляющий функцию от комплексного переменного
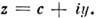С помощью комплексного потенциала скоростей изучаются безотрывное обтекание
плоского контура, струйное обтекание стенок и волновое движение. Безотрывное
П. т. вокруг плоского контура может быть бесциркуляционным или циркуляционным.
В первом случае результирующее воздействие жидкости на плоский контур равно
нулю (см. Д-Аламбера - Эйлера парадокс), во втором - результирующее
воздействие потока жидкости на контур сводится к подъёмной силе, а в
случае струйного П. т. вокруг плоского контура - к силе сопротивления, пропорциональной
квадрату скорости. П. т. имеет место также при движениях сжимаемой жидкости
или газа, представляющих собой малые возмущения нек-рого известного состояния
равновесия пли движения, напр. при распространении звука в среде; при этом малый
избыток давления над давлением в состоянии равновесия среды связан с потенциалом
скоростей соотношением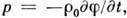 
а из ур-ния неразрывности в случае, когда потенциал массовых сил не зависит
от времени, получается волновое ур-ние
где с - скорость распространения звука,
вычисленная для невозмущённого состояния покоя: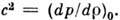
Для П. т. газа при адиабатич. законе дифференц. ур-ние для потенциала скоростей
становится нелинейным, но с помощью преобразования С. А. Чаплыгина оно приводится
к линейному ур-нию, разрешаемому в ряде случаев.
1. Электромагнитная волна (в религиозной терминологии релятивизма - "свет") имеет строго постоянную скорость 300 тыс.км/с, абсурдно не отсчитываемую ни от чего. Реально ЭМ-волны имеют разную скорость в веществе (например, ~200 тыс км/с в стекле и ~3 млн. км/с в поверхностных слоях металлов, разную скорость в эфире (см. статью "Температура эфира и красные смещения"), разную скорость для разных частот (см. статью "О скорости ЭМ-волн")
2. В релятивизме "свет" есть мифическое явление само по себе, а не физическая волна, являющаяся волнением определенной физической среды. Релятивистский "свет" - это волнение ничего в ничем. У него нет среды-носителя колебаний.
3. В релятивизме возможны манипуляции со временем (замедление), поэтому там нарушаются основополагающие для любой науки принцип причинности и принцип строгой логичности. В релятивизме при скорости света время останавливается (поэтому в нем абсурдно говорить о частоте фотона). В релятивизме возможны такие насилия над разумом, как утверждение о взаимном превышении возраста близнецов, движущихся с субсветовой скоростью, и прочие издевательства над логикой, присущие любой религии.
4. В гравитационном релятивизме (ОТО) вопреки наблюдаемым фактам утверждается об угловом отклонении ЭМ-волн в пустом пространстве под действием гравитации. Однако астрономам известно, что свет от затменных двойных звезд не подвержен такому отклонению, а те "подтверждающие теорию Эйнштейна факты", которые якобы наблюдались А. Эддингтоном в 1919 году в отношении Солнца, являются фальсификацией. Подробнее читайте в FAQ по эфирной физике.
|
|
 |
