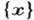 ,
проведённых независимо, рассматривают как случайные переменные, распределённые
с плотностью вероятности
,
проведённых независимо, рассматривают как случайные переменные, распределённые
с плотностью вероятности 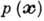 , к-рая может быть дискретной либо непрерывной.
, к-рая может быть дискретной либо непрерывной.Анализ данных - дисциплина, посвящённая построению и исследованию процедур, осуществляющих преобразование от "исходных
данных" к "результату". Ранее вместо термина "А. д."
употреблялся термин "обработка результатов наблюдений (измерений)".
Матем. аппаратом А. д. является матем. статистика.
Под "исходными данными"
обычно понимают нек-рый первичный набор чисел, получаемых в процессе проведения
исследования: результаты измерений к--л. физ. величины; совокупность параметров,
характеризующих к--л. событие или состояние системы, установки, физ. тела; число
случаев осуществления к--л. события; счёт наличия или отсутствия к--л. признака
и т. п.
Результатами А. д. обычно являются либо
итоговые показатели (напр., при обработке многократных измерений к--л. физ.
величин), либо параметры модели (физ. закономерности), описывающей исследуемое
явление (напр., размеры ядер при исследовании распределений углов рассеяния
частиц на ядрах), либо вывод о справедливости к--л. теории и т. п.
Погрешности данных. Как исходные данные,
так и результаты помимо своей величины характеризуются ошибкой,
или погрешностью. Под ошибкой обычно понимают разницу между наблюдаемой или
вычисляемой величиной и фактич. величиной. Ошибки в исходных данных могут от
опыта к опыту систематически повторяться (т. н. систематические ошибки) либо
меняться случайным образом (т.н. случайные ошибки).
Систематич. ошибки, как правило, связаны
с неправильно откалиброванным измерит. прибором (или невозможностью калибровки),
с неправильно учтёнными, внеш. условиями проведения опыта (или невозможностью
их учёта), с неправильной методикой измерения и т. п. Напр., в прецизионных
опытах по измерению полного сечения рассеяния частиц высокой энергии на протонах
осн. вклад в систематич. ошибку даёт неточное знание плотности жидкого водорода,
к-рый используется в качестве мишени. Исследование систематич. ошибок играет
важную роль в анализе эксперим. данных. После выявления природы систематич.
ошибок и определения их величины они перестают быть ошибками и становятся поправками.
Если систематич. ошибки устранить не удаётся, то обычно оценка систематич. ошибки
приводится совместно с результатом.
Случайные ошибки измерений - флуктуации
в наблюдениях (измерениях) -являются следствием конечной точности эксперимента
(измерит. прибора) и (или) случайного характера наблюдаемой (измеряемой) величины.
Получению численных результатов по данным измерений, содержащим случайные ошибки,
посвящён раздел матем. статистики, наз. теорией ошибок (см. Ошибок теория). В исходных данных и в результатах анализа могут быть также и грубые ошибки
(промахи) - следствие неправильных записей, неумелого применения прибора, применения
испорченного прибора, арифме-тич. ошибок в вычислениях и т. п. Такие ошибки
исправляют при более тщательном повторении опытов или расчётов.
Из-за наличия в реальных исходных данных
всевозможных ошибок неизвестного характера на практике сложно сформулировать
и построить такую процедуру, к-рая приведёт к окончат. результату. Поэтому А.
д. обычно подразделяют на два раздела (этапа): исследование данных и обработка
данных.
Исследование данных (или разведочный
анализ) - это такие операции, выполнение к-рых существенно зависит от конкретных
данных. При исследовании данных определяющую роль играет человек, к-рый решает:
как дальше поступать с этими данными; какие точки выбросить, какие оставить;
какую конкретную процедуру применить для улучшения качества исходных данных;
нужно ли сгруппировать ряд данных и как это сделать и т. п. В разведочном анализе
обычно используют простые методы преобразования и представления данных, позволяющие
качественно оценить имеющиеся данные и повысить их надёжность (достоверность).
Из осн. процедур разведочного анализа следует особенно отметить процедуру "сглаживания",
устранение грубых ошибок.
Обработка данных - это собственно процедура
получения результатов по выбранной схеме. Матем. статистика в осн. посвящена
именно обработке данных.
Статистический анализ. Из-за конечной
точности измерений и наличия случайных ошибок или из-за стати-стич. природы
эксперим. данных ряд измерений 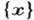 ,
проведённых независимо, рассматривают как случайные переменные, распределённые
с плотностью вероятности
,
проведённых независимо, рассматривают как случайные переменные, распределённые
с плотностью вероятности 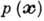 , к-рая может быть дискретной либо непрерывной.
, к-рая может быть дискретной либо непрерывной.
Задача эксперим. исследований - получить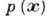 по наблюдениям
по наблюдениям 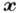 ,
задача теории - придумать (вычислить)
,
задача теории - придумать (вычислить) 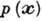 . При таком рассмотрении почти все задачи А. д. сводятся к оцениванию плотности
вероятности и к определению согласия между теоретич. и эмпирич. распределениями.
В матем. статистике задачам оценивания
посвящён раздел статистич. оценивания, а задачам определения согласия - раздел
статистич. проверки гипотез. По способу оценивания плотности вероятности и определения
её согласия с теоретич. А. д. подразделяют на параметрический и непараметрический.
. При таком рассмотрении почти все задачи А. д. сводятся к оцениванию плотности
вероятности и к определению согласия между теоретич. и эмпирич. распределениями.
В матем. статистике задачам оценивания
посвящён раздел статистич. оценивания, а задачам определения согласия - раздел
статистич. проверки гипотез. По способу оценивания плотности вероятности и определения
её согласия с теоретич. А. д. подразделяют на параметрический и непараметрический.
В непара метри ч. анализе предполагается,
что нет никакой априорной информации относительно вида функции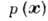 . Заключение о функции
. Заключение о функции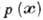 или о её свойствах делается непосредственно из исходных данных. Построение гистограмм - один из примеров непараметрического оценивания плотности вероятности.
или о её свойствах делается непосредственно из исходных данных. Построение гистограмм - один из примеров непараметрического оценивания плотности вероятности.
В параметрич. анализе предполагается,
что 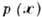 входит в параметрич.
семейство распределения
входит в параметрич.
семейство распределения 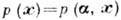 , где
, где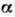 -конечный набор
параметров (дискретных или непрерывных), к-рые выделяют отд. распределения из
семейства. Здесь проблема оценивания функции
-конечный набор
параметров (дискретных или непрерывных), к-рые выделяют отд. распределения из
семейства. Здесь проблема оценивания функции 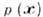 сводится к выбору подходящих значений
сводится к выбору подходящих значений 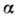 .
Простейшая задача параметрич. анализа-получение результата для к--л. физ. величины
по данным её многократных измерений со случайной ошибкой, соответствующей Гаусса
распределению ошибок. Пусть имеется ряд хi, i=1, 2, . ..,N измерений одной и той же физ. величины с дисперсией
.
Простейшая задача параметрич. анализа-получение результата для к--л. физ. величины
по данным её многократных измерений со случайной ошибкой, соответствующей Гаусса
распределению ошибок. Пусть имеется ряд хi, i=1, 2, . ..,N измерений одной и той же физ. величины с дисперсией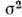 .
Вероятность одиночного наблюдения хi равна
.
Вероятность одиночного наблюдения хi равна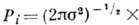 X
X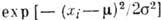 , тогда вероятность
N независимых наблюдений хi, i = l, 2, ..., N, равна
произведению вероятностей
, тогда вероятность
N независимых наблюдений хi, i = l, 2, ..., N, равна
произведению вероятностей
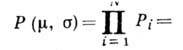
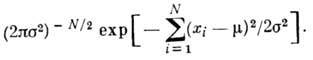
Согласно максимального правдоподобия
методу в качестве оценки результата измерений физ. величины х, при
пост. дисперсии ,
следует взять такую величину
,
следует взять такую величину 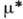 ,
к-рая даёт максимум вероятности
,
к-рая даёт максимум вероятности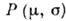 . Максимум предыдущего выражения достигается при минимуме показателя экспоненты,
откуда следует, что
. Максимум предыдущего выражения достигается при минимуме показателя экспоненты,
откуда следует, что 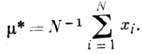
Проверка гипотез. Результатом
А. д. может быть также оценка справедливости к--л. теоретич. модели или гипотезы
(см. Статистическая гипотеза)в смысле применимости её к экспериментально
наблюдаемому явлению. Такой результат сам по себе не даёт доказательства справедливости
теории, он даёт лишь возможность выбора альтернатив и степень согласия теории
и эксперимента.
Пусть надо проверить гипотезу Н0
по отношению к гипотезе Н1 на основании нек-рых эксперим.
наблюдений 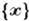 . Пусть
. Пусть
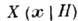 есть функция наблюдений
и проверяемой гипотезы (X обычно наз. проверочной статистикой) и пусть
есть функция наблюдений
и проверяемой гипотезы (X обычно наз. проверочной статистикой) и пусть
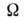 есть пространство
всевозможных значений X. Пространство
есть пространство
всевозможных значений X. Пространство 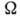 делят на две области
делят на две области 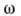 и
и
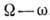 , к-рые соответственно
наз. критической и допустимой. Считают, что при попадании проверочной статистики
X в критич. область
, к-рые соответственно
наз. критической и допустимой. Считают, что при попадании проверочной статистики
X в критич. область 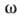 гипотеза Н0 неверна (верна Н1), а при попадании
X в допустимую область гипотеза Н0 верна (Н1 ошибочна).
гипотеза Н0 неверна (верна Н1), а при попадании
X в допустимую область гипотеза Н0 верна (Н1 ошибочна).
Разделение пространства 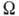 на критическую и допустимую области обычно производится так, чтобы вероятность
отвергнуть гипотезу, когда она верна (т. е. вероятность потери), была бы малой.
Величину этой вероятности наз. уровнем значимости или величиной критерия. Т.
о., уровень значимости
на критическую и допустимую области обычно производится так, чтобы вероятность
отвергнуть гипотезу, когда она верна (т. е. вероятность потери), была бы малой.
Величину этой вероятности наз. уровнем значимости или величиной критерия. Т.
о., уровень значимости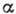 равен вероятности попадания X в
равен вероятности попадания X в 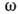 ,
когда гипотеза Н0 верна, т. е.
,
когда гипотеза Н0 верна, т. е. 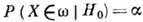 .С др. стороны, целесообразно потребовать также малости вероятности принятия
ложной гипотезы,
.С др. стороны, целесообразно потребовать также малости вероятности принятия
ложной гипотезы, 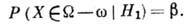 т. е. вероятности примеси
т. е. вероятности примеси 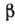 :
:
Для оценки критерия проверки альтернативных
гипотез (см. Статистический критерий)служит величина, наз. мощностью
критерия, к-рая определяется как вероятность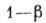 попадания X в критич. область пространства
попадания X в критич. область пространства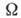 ,
когда верна гипотеза Н1 т.е.
,
когда верна гипотеза Н1 т.е. 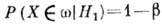 . При выборе гипотезы исследователь обычно решает, какие потери
. При выборе гипотезы исследователь обычно решает, какие потери 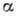 он
может допустить, а затем выбирает проверочную статистику и критич. область так,
чтобы максимизировать мощность критерия
он
может допустить, а затем выбирает проверочную статистику и критич. область так,
чтобы максимизировать мощность критерия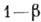 .
.
Одна из наиб. общих проверяемых гипотез
при А. д. состоит в том, что плотность вероятности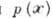 есть данная функция
есть данная функция 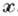 ,
т. е.
,
т. е. 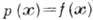 . Здесь обычно
нет определ. альтернативной гипотезы, т. е. фактически имеется набор всевозможных
альтернативных гипотез, к-рые явно не определены. В этом случае невозможно вычислить
примесь и определить мощность критерия. Такая задача возникает при проверке
совпадения эксперим. данных с к--л. теоретич. моделью и решается на основе критерия
согласия. Как при обычной проверке гипотез, начинают с выбора проверочной статистики,
однако пространство W
не делится на критич. и допустимую области. Уровень значимости здесь определяется
как вероятность того, что при условии Н0 проверочная статистика
X будет иметь значение, превышающее величину Т, наблюдаемую из
данных,
. Здесь обычно
нет определ. альтернативной гипотезы, т. е. фактически имеется набор всевозможных
альтернативных гипотез, к-рые явно не определены. В этом случае невозможно вычислить
примесь и определить мощность критерия. Такая задача возникает при проверке
совпадения эксперим. данных с к--л. теоретич. моделью и решается на основе критерия
согласия. Как при обычной проверке гипотез, начинают с выбора проверочной статистики,
однако пространство W
не делится на критич. и допустимую области. Уровень значимости здесь определяется
как вероятность того, что при условии Н0 проверочная статистика
X будет иметь значение, превышающее величину Т, наблюдаемую из
данных, 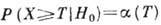 В данном
контексте величина
В данном
контексте величина  наз. также уровнем достоверности.
наз. также уровнем достоверности.
Критерий согласия конструируется при
помощи меры различия между непараметрич. оценкой плотности вероятности (чаще
всего гистограммой) и теоретич. функцией плотности вероятности проверяемой гипотезы.
Наиб. популярной является квадратич. мера, нормированная на дисперсию. В достаточно
общих предположениях проверочная статистика сводится к сумме квадратов независимых,
нормально распределённых случайных величин с нулевым средним и единичной дисперсией,
к-рая имеет 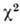 -распределение
с числом степеней свободы, равным кол-ву членов в сумме. В этом случае критерием
согласия является
-распределение
с числом степеней свободы, равным кол-ву членов в сумме. В этом случае критерием
согласия является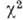 -критерий
Пирсона.
-критерий
Пирсона.
Использование ЭВМ. Совр. эксперим. исследования
в области ядерной физики, геофизики, физики атмосферы, океана и др. характеризуются
огромным объёмом получаемой первичной информации (до 1012 бит/с и
более). Результаты эксперимента обычно составляют ~103 бит. Т. о.,
в процессе А. д. происходит значит. сжатие информации (в 1 млрд. раз и более).
А. д. таких эксперим. исследований немыслим без использования средств автоматизации
и быстродействующей вычислит. техники (см. Автоматизация эксперимента ).Каждый
эксперимент во времени проходит два этапа: получение данных и получение результатов.
Совр. автоматизиров. эксперим. установки, оснащённые вычислит. техникой, позволяют
решать часть задач А. д. уже в процессе их получения, т. е. в реальном масштабе
времени проведения измерений. Этот этап А. д. обычно наз. анализом в реальном
масштабе времени или анализом "в линию".
Целью и смыслом анализа "в линию"
является всеобъемлющий контроль за работой эксперим. установки и ходом эксперимента
в целом. Наиб. эфф. вид контроля - контроль по конечным результатам. Такой метод
контроля избавляет от трудоёмких исследований зависимостей свойств установки
от неск. тысяч параметров, от необходимости выбирать и устанавливать допуски
на изменение этих параметров и комбинации этих изменений. Повышается и надёжность
установки, т. к. имеется возможность оперативно принимать решения о необходимости
и целесообразности ремонта при отказе отд. элементов или о продолжении работы
с ухудшенными характеристиками. Часто для проверки правильности работы установки
и её отд. узлов создают спец. тестовые и контрольные средства, однако обычно
осуществляют оба типа контроля.
Иногда проводят предварит. обработку
"в линию" всей поступающей информации для её сжатия перед записью
и последующим анализом. Анализ "в линию" позволяет получать физ.
результат эксперимента хотя бы на части исходных данных. Однако окончательно
все задачи А. д. практически невозможно решить в процессе их получения из-за
необходимости проведения исследования данных, к-рое имеет характер последоват.
приближений.
Окончат. результаты эксперимента обычно
получают в процессе последующего анализа. При этом для получения окончат. результатов
часто требуется выполнение дополнительных, т. н. калибровочных, опытов (для
исследования и устранения систематич. ошибок) либо сопоставление получаемых
результатов с результатами др. экспериментов. Методы полного (последующего)
анализа обычно более богаты, чем при выборочном анализе "в линию".
Здесь имеются неогранич. возможности повторения последоват. приближений по исходным
данным. В этом смысле А. д.- бесконечный процесс ("способ существования
данных"). Следует особо выделить графическое представление данных: из рисунков и графиков часто можно добыть информацию, неожиданную для исследователя.

С. В. Клименко, А. А. Лебедев
|
|