© 2008 Алексей Померанцев
|
В этом пособии рассмотрены основные методы, применяемые для решения задач калибровки (называемой также градуировкой). Текст ориентирован, прежде всего, на специалистов в области анализа экспериментальных данных: химиков, физиков, биологов, и т.д. Он может служить пособием для исследователей, начинающих изучение этого вопроса. Продолжить исследования можно с помощью указанной литературы. В пособии интенсивно используются понятия и методы матричной алгебры – вектор, матрица, и т.п. Читателям, которые плохо знакомы с этим аппаратом, рекомендуется изучить, или, хотя бы просмотреть, пособие "Матрицы и векторы". Изложение иллюстрируется примерами, выполненными в рабочей книге Excel “Calibration.xls”, которая сопровождает этот документ. Предполагается, что читатель имеет базовые навыки работы в среде Excel, умеет проводить простейшие матричные вычисления с использованием функций листа, таких как МУМНОЖ, ТЕНДЕНЦИЯ и т.п. Освежить эти знания можно с помощью пособия Матричные операции в Excel. Важная информация о работе с файлом Calibration.xls Ссылки на примеры помещены в текст как объекты Excel. По форме эти примеры имеют абстрактный, модельный характер, однако, по своей сути, они тесно связаны с задачами, встречающимися на практике. |
Суть задачи калибровки состоит в следующем. Пусть имеется некоторая переменная (свойство) y, величину которой необходимо установить. Однако, по ряду обстоятельств (недоступность, дороговизна, длительность), прямое измерение величины y невозможно. В то же время можно легко (быстро, дешево) измерить другие величины: x=(x1, x2, x3,…), которые связаны с искомой величиной y. Задача калибровки состоит в установлении количественной связи между переменными x и откликом y –
y=f(x1, x2, x3,…| a1, a2, a3,…) +ε
На практике это означает:
(1) подбор вида зависимости f, и ...
(2) оценку неизвестных параметров a1, a2, a3,… в этой калибровочной зависимости.
Разумеется, калибровку нельзя построить абсолютно точно. В дальнейшем мы увидим, что это не только невозможно, но и опасно. В калибровочной зависимости всегда присутствуют погрешности (ошибки) ε, источник которых – пробоотобор, измерения, моделирование, и т.д.
Простейший пример калибровки дает общеизвестный прибор, называемый безменом, т.е. пружинные весы. Искомая величина y – это вес образца, а x – это удлинение пружины весов. Закон Гука –
y=ax + ε,
связывает y и x через коэффициент жесткости пружины a, который априори неизвестен. Процедура калибровки очень проста – взвешиваем стандартный образец весом в 1 кг и отмечаем на шкале удлинение пружины, затем используем образец в 2 кг, и т.д. В результате этой калибровки (точнее, градуировки) получается шкала, по которой можно определить вес нового, нестандартного образца.
Этот элементарный пример демонстрирует основные черты процедуры калибровки, которые подробно будут рассмотрены далее. Во-первых, для калибровки необходимы несколько стандартных образцов, для которых величины y известны заранее. Во-вторых, диапазон, в котором предполагается измерять показатель y, должен полностью покрываться этими калибровочными образцами. Действительно, нельзя измерять образцы весом более 5 кг, если в калибровке использовались образцы, весом менее чем 5 кг.
Разумеется, на практике все обстоит не так просто, как в этом элементарном примере. Например, в калибровке может участвовать не один показатель y (отклик), а несколько откликов y1, y2,..... yK, которые нас интересуют. Все возможные особенности, различные трудности, сопутствующие процедуре калибровке будут рассмотрены далее. Сейчас же мы подведем первые итоги и сформулируем задачу калибровки в общем виде.
Пусть имеется матрица Y, размерностью (I×K), где I – это число стандартных образцов (сравнения), использованных в калибровке, а K – это число одновременно калибруемых откликов. Матрица Y содержит значения откликов y, известные из независимых экспериментов (референтные или стандартные значения). Пусть, с другой стороны, имеется соответствующая матрица переменных X размерностью (I×J), где I – это, естественно, тоже число образцов, а J – это число независимых переменных (каналов), используемых в калибровке. Матрица X состоит из альтернативных, как правило, многоканальных (J>>1) измерений. Используя калибровочные данные (X, Y), требуется построить функциональную связь между Y и X.
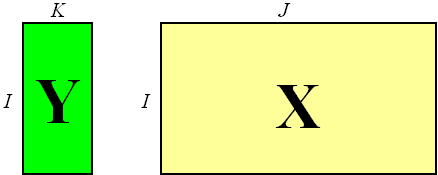
Рис. 1 Калибровочный набор данных
Итак, задача калибровки состоит в построении математической модели, связывающей блоки X и Y, с помощью которой можно в дальнейшем предсказывать значения показателей y1, y2,..... yK, по новой строке значений аналитического сигнала x.
Теоретически функциональная связь между переменными x и y может быть сложной, например,
y=b0 exp(b1x+b2x2) + ε .
Однако на практике большинство используемых калибровок являются линейными, т.е. имеют вид –
y=b0 + b1x1 + b2x2+...+ bJxJ + ε .
Заметим, что термин "линейность" употребляется в контексте этого пособия вместо более правильного термина "билинейность", означающего линейность как по отношению к переменным x, так и в отношении коэффициентов b. Поэтому, калибровка
y=b0 + b1x + b2x2 + ε .
является нелинейной, несмотря на то, что она легко "линеаризуется" введением новой переменной x2=x2.
Главное преимущество билинейной модели – это единственность, тогда как все прочие калибровки образуют бесконечное множество, выбор из которого затруднителен. В этом пособии рассматриваются только линейные калибровки вида –
Читатели, заинтересованные в изучении нелинейных методов анализа данных могут обратиться к описанию программы Fitter.
Предпочтение (би)линейных, формальных моделей, не отягощенных дополнительным физико-химическим смыслом, является магистральным направлением развития хемометрики. Такой подход позволяет исключить влияние субъективного фактора, проявляющегося при выборе калибровочной зависимости. Однако за это приходится расплачиваться – все линейные модели имеют ограниченную область применения.
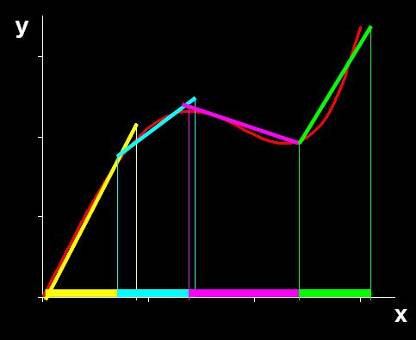
Рис. 2 Линеаризация калибровки
Суть дела иллюстрирует Рис. 2, где показаны четыре участка, на которых сложная нелинейная зависимость приближается простыми линейными моделями. Каждая из этих моделей работает только на своей области переменной x и выход за ее границы приводит к грубым ошибкам. Принципиальным моментом здесь является то, какую область можно считать допустимой – иначе говоря, насколько широко можно применять калибровочную модель. Ответ на этот вопрос дают методы проверки (валидации).
|
|