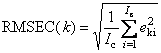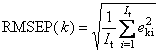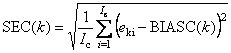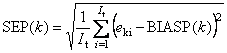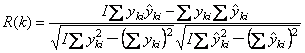MatLab калибровка ДМ экономическая информатика визуальные среды - 4GL Теория и практика обработки информации

Калибровка

1.3. Калибровка и проверка

1.4. "Качество" калибровки

1.5. Неопределенность, точность и воспроизводимость

1.6. Недооценка и переоценка

1.7. Мультиколлинеарность

1.8. Подготовка данных

1.3. Калибровка и проверка

При надлежащем построении калибровочной модели исходный массив данных состоит из двух независимо полученных наборов, каждый из которых является достаточно представительным. Первый набор, называемый обучающим, используется для идентификации модели, т.е. для оценки ее параметров. Второй набор, называемый проверочным, служит только для проверки модели. Построенная модель применяется к данным из проверочного набора, и полученные результаты сравниваются с проверочными значениями. Таким образом принимается решение о правильности, точности моделирования методом тест-валидации.

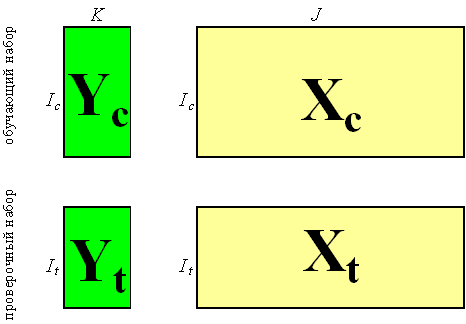
Рис. 3 Обучающий и проверочный наборы

В некоторых случаях объем данных слишком мал для такой проверки. Тогда применяют другой метод – перекрестной проверки (кросс-валидация, скользящая проверка). В этом методе проверочные значения вычисляют с помощью следующей процедуры.

Некоторую фиксированную долю (например, первые 10% образцов) исключают из исходного набора данных. Затем строят модель, используя только оставшиеся 90% данных, и применяют ее к исключенному набору. На следующем цикле исключенные данные возвращаются, и удаляется уже другая порция данных (следующие 10%), и опять строится модель, которая применяется к исключенным данным. Эта процедура повторяется до тех пор, пока все данные не побывают в числе исключенных (в нашем случае – 10 циклов). Наиболее (но неоправданно) популярен вариант перекрестной проверки, в котором данные исключаются по одному (Leave-One-Out – LOO).

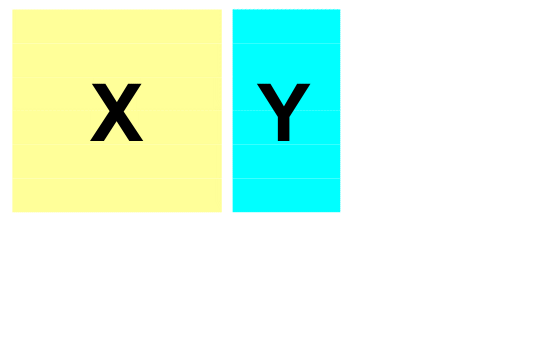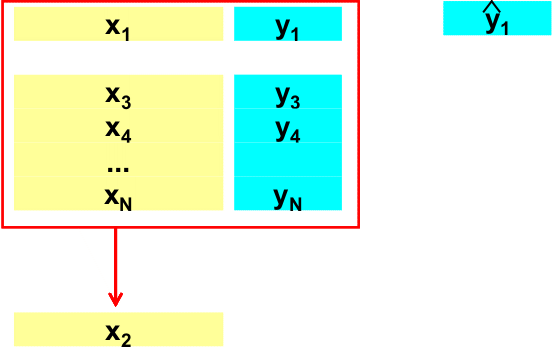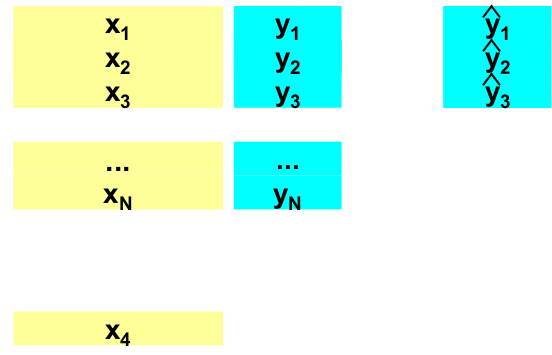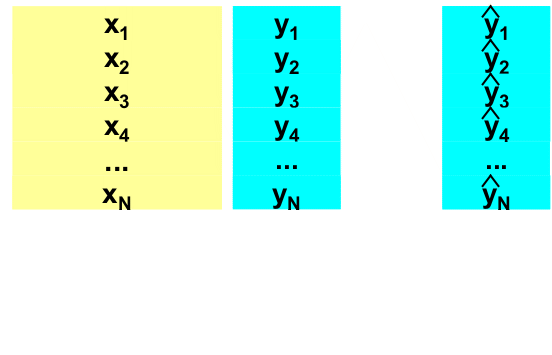
Рис. 4 Метод перекрестной проверки

Используется также проверка методом корректировки размахом, суть которой предлагается изучить самостоятельно по книгам.

1.4. "Качество" калибровки

Результатом калибровки являются величины – оценки стандартных откликов Y_c, найденные по модели, построенной на обучающем наборе. Результатом проверки служат величины – оценки проверочных откликов Y_t, вычисленные по той же модели. Отклонение оценки от стандарта (проверочного значения) вычисляют как матрицу остатков: в обучении , и в проверке .

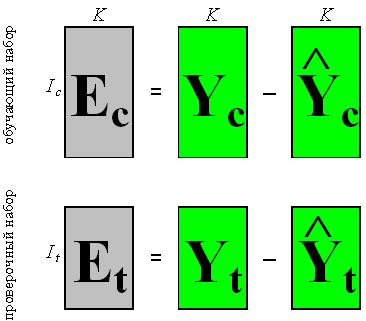
Рис. 5 Остатки в обучении и в проверке

Следующие величины характеризуют "качество" калибровки в среднем.

Полная дисперсия остатков в обучении (TRVC) и в проверке (TRVP) –

(2)

Эти величины вычисляются по формуле (10) в пособии Статистика, для m=0.

Объясненная дисперсия остатков при обучении (ERVC) и при проверке (ERVP) –

(3)

Среднеквадратичные остатки калибровки (RMSEC) и проверки (RMSEP) –

(4)

Величины RMSE зависят от k – номера отклика.

Смещение в калибровке (BIASC) и в проверке (BIASP) –

(5)

Величины BIAS зависят от k – номера отклика.

Стандартные ошибки в калибровке (SEC) и в проверке (SEP) –

(6)

Величины SE зависят от k – номера отклика. Они вычисляются по формуле (9) из пособия Статистика.

Коэффициенты корреляции R²между стандартными y_ki и оцененными 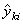откликами. Они также вычисляется отдельно для обучающего 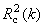и проверочного 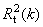наборов.

(7)

Величины R² зависят от k – номера отклика.

Во всех этих формулах величины e_ki – это элементы матриц E_c или E_t. Для характеристик, наименование которых оканчивается на C (например, RMSEC), используется матрица E_c (обучение), а для тех, которые оканчиваются на P (например, RMSEP), берется матрица E_t (проверка).

1.5. Неопределенность, точность и воспроизводимость

Такое большое число показателей, характеризующих качество калибровки, объясняется не только историческими причинами, но и тем, что они отражают различные свойства неопределенности при обучении, и при проверке (прогнозе). Для объяснения этих показателей необходимо ввести понятия воспроизводимости (прецизионности) и точности.

Воспроизводимость (precision) характеризует то, насколько близко находятся друг от друга независимые повторные измерения.

Точность (accuracy) определяет степень близости оценок к истинному (стандартному) значению y.

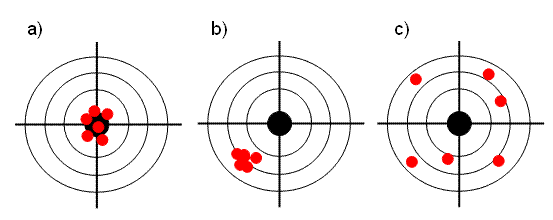
Рис.6 Точность и воспроизводимость

Рис. 6 объясняет суть дела. Графики a) и b) представляют оценки с хорошей воспроизводимостью. Вариант a) , кроме того, обладает и высокой точностью, что, разумеется, нельзя сказать о графике c). В последнем случае и воспроизводимость, и точность оставляют желать лучшего.

Показатели SEC и SEP характеризуют воспроизводимость калибровки, тогда как RMSEC и RMSEP показывают ее точность. Величины BIASC и BIASP определяют смещение калибровки относительно истинного значения (Рис. 6b). Можно показать, что –

RMSE² = SE² + BIAS².

(8)

Таким образом, при построении калибровки предпочтение следует отдавать показателям RMSE, а не SE.

Показатели TRV и ERV характеризуют ситуацию "в целом", без различения калибруемых откликов, т.е.

(9)

1.6. Недооценка и переоценка

При построении калибровки исследователь часто имеет возможность последовательного усложнения модели. Приведем простейший пример, иллюстрирующий этот процесс.

Из курса школьной физики известно, что расстояние L, на которое летит снаряд, выпущенный со скоростью v из орудия, наклоненного под углом α к горизонту, равно –

L=v²sin(2α)/g.

Предположим, что у нас имеются экспериментальные данные L(α ).

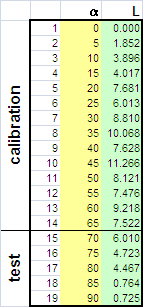
Рис.7Данные для артиллерийского примера

Забудем о том, что функциональная связь между L (т.е., y) и α (т.е., x) нам известна, и попробуем построить формальную полиномиальную калибровку –

L=b₀+ b₁α + b₂α² +…. b_n αⁿ+ ε

по этим данным. На Рис. 8а показано, как описываются обучающие () и проверочные () данные моделями при n=0, 1, .., 5. Видно, что при недостаточной сложности модели (n = 0, 1) обучающие данные лежат далеко от модели. Это – случай недооценки. Когда сложность модели увеличивается, то согласие между обучающими данными и моделью улучшается. Однако, при излишней сложности (n = 4, 5), модель все хуже работает при прогнозе на проверочный набор. Это – случай переоценки.

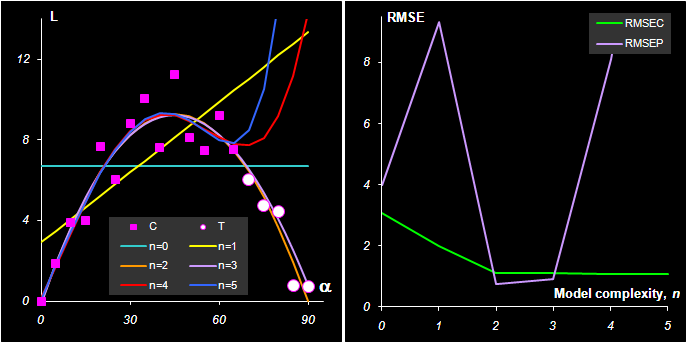
Рис.8 Артиллерийский пример. a)Калибровка, b)Среднеквадратичные остатки обучения (RMSEC)и проверки (RMSEP)

На Рис. 8b показано, как изменяются показатели RMSEC и RMSEP при увеличении сложности модели. Это – типичный график, в котором RMSEC монотонно падает, а RMSEP проходит через минимум. Именно точка минимума RMSEP позволяет определить оптимальную сложность модели. В нашем случае – это 2. Теперь мы можем вспомнить о содержательной модели, которая хорошо аппроксимируется полиномом второй степени по α –

L=v²/g sin(2α) ≈ Const α(α – π/4)

В задачах многомерной калибровки недооценка и переоценка проявляются через выбор числа скрытых, главных компонент. Когда их число мало, модель плохо приближает обучающий набор и при увеличении сложности модели RMSEC монотонно уменьшается. Однако качество прогноза на проверочный набор может при этом ухудшаться (U-образная форма RMSEP). Точка минимума RMSEP, или начало плато, соответствует оптимальному числу главных компонент. Проблема сбалансированности описания данных рассматривается во многих работах А. Хоскюлдссона, который в 1988 году ввел новую концепцию моделирования – так называемый H-принцип. Согласно этому принципу точность моделирования (RMSEC) и точность прогнозирования (RMSEP) связаны между собой. Улучшение RMSEC неминуемо влечет ухудшение RMSEP, поэтому их нужно рассматривать совместно. Именно по этой причине множественная линейная регрессия, в которой всегда участвует явно избыточное число параметров, неизбежно приводит к неустойчивым моделям, непригодным для практического применения.

1.7. Мультиколлинеарность

Рассмотрим задачу множественной линейной калибровки

Y = XB .

(10)

Разумеется, здесь мы имеем дело с обучающим набором данных. Мы не пишем индекс у матриц (Y_с, X_с) только для простоты обозначений. Классическое решение этой задачи находится с помощью метода наименьших квадратов. Минимизируя сумму квадратов отклонений (Y – XB)^t(Y – XB), получаем оценки неизвестных коэффициентов B –

(11)

Далее находится –

(12)

– оценка искомых откликов. Главная проблема при таком классическом подходе – это обращение матрицы X^tX . Очевидно, что если число стандартных образцов меньше, чем число переменных (I<J) то то обратной матрицы не существует. Более того, даже при достаточно большом числе образцов (I>J), обратной матрицы может и не быть. Рассмотрим простейший пример.

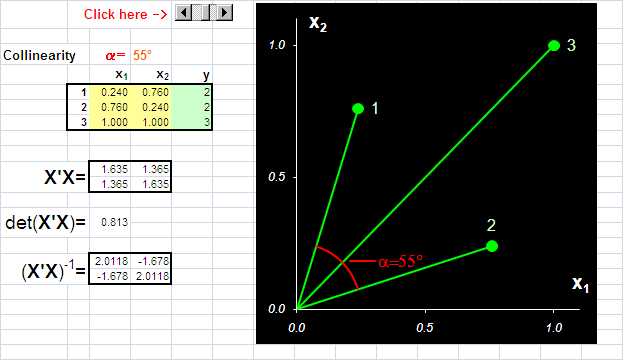
Рис.9 Пример коллинеарных данных

На Рис. 9 представлены данные, в которых всего три образа (I=3) и две переменные (J=2). Используя активный элемент на листе, угол между векторами 1 и 2 можно изменять от 90^о до 0^о. Чем меньше угол, тем меньше детерминант матрицы X^tX и тем хуже определяется матрица (X^tX)^–1. В предельном случае, когда угол между векторами равен 0^о, матрица X^tX не может быть обращена. При этом векторы 1 и 2 колинеарны, т.е. они лежат на одной прямой, совпадающей с вектором 3. Анимация на Рис. 10 иллюстрирует суть проблемы – невозможность построения калибровки классическим способом, когда данные коллинеарны.

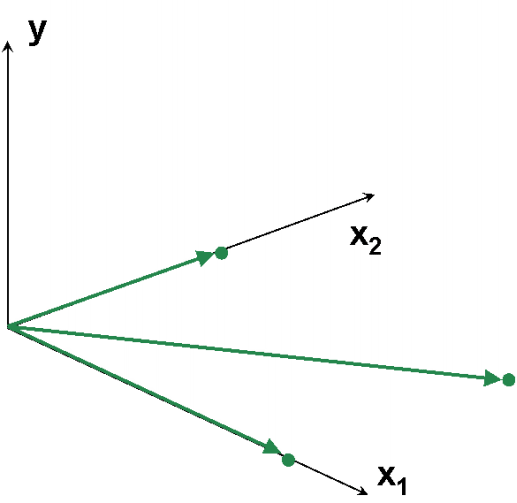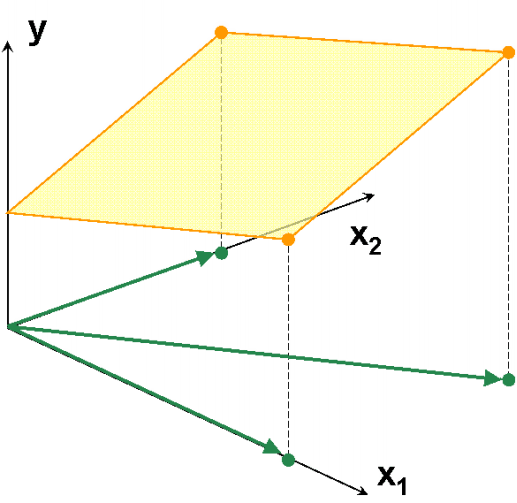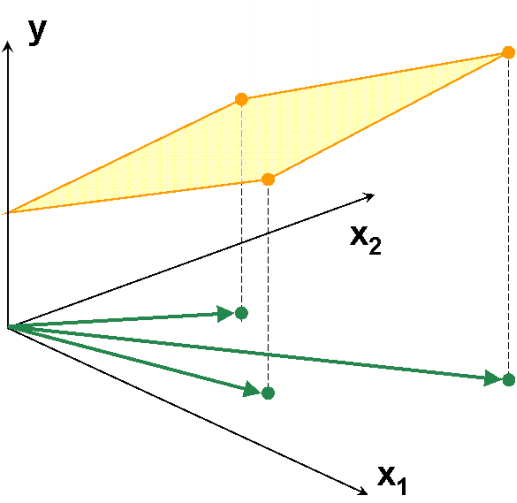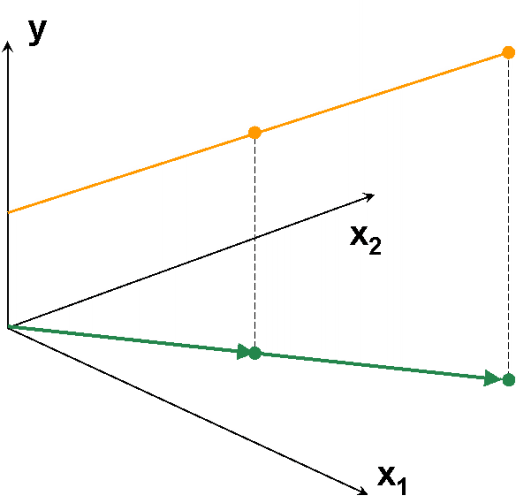
Рис.10 Пример коллинеарных данных

В многомерной калибровке (т.е. при J>> 1), мы все время сталкиваемся с мультиколлинеарностью – множественными связями между векторами X-переменных, приводящими к той же проблеме – невозможности обращения матрицы X^tX. Далее мы увидим, что можно сделать в случае мультиколлинеарности данных.

1.8. Подготовка данных

Важным условием правильного моделирования и, соответственно, успешного анализа, является предварительная подготовка данных, которая включает различные преобразования исходных, "сырых" экспериментальных значений. Простейшими преобразованиями является центрирование и нормирование.

Центрирование – это вычитание из исходной матрицы X матрицы M, т.е.

Обычно усреднение проводится по столбцам: для каждого вектора x_j вычисляется среднее значение –

Тогда M=(m₁1,..., m_J1), где 1 – это вектор из единиц размерности I.

Центрирование – это почти обязательная процедура перед применением проекционных методов. Второе простейшее преобразование данных, нормирование, не является обязательным. Нормирование, в отличие от центрирования, не меняет структуру данных, а просто изменяет вес различных частей данных при обработке. Чаще всего применяется нормирование по столбцам – это умножение исходной матрицы X справа на матрицу W, т.е.

Матрица W – это диагональная матрица размерности J×J. Обычно диагональные элементы w_jj равны обратным значениям стандартного отклонения –

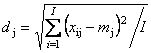вычисленным для каждого столбца x_j. Нормирование по строкам (называемое также нормализацией) – это умножение матрицы X слева на диагональную матрицу W, т.е.

При этом размерность W равна I×I, а ее элементы w_ii – это обратные значения стандартных отклонений строк x_i^t.

Комбинация центрирования и нормирования по столбцам

называется автошкалированием. Нормирование данных часто применяют для того, чтобы уравнять вклад в модель от различных переменных (например, в гибридном методе ЖХ-МС), учесть неравномерные погрешности, или для того, чтобы обрабатывать совместно разные блоки данных. Нормирование также можно рассматривать как метод, позволяющий стабилизировать вычислительные алгоритмы. В тоже время, к этому преобразованию нужно относиться с большой осторожностью, т.к. оно может сильно исказить результаты качественного анализа. Любое преобразование данных – центрирование, шкалирование, и т.п. – всегда делается сначала на обучающем наборе. По этому набору находятся значения m_j и d_j, которые затем применяются и к обучающему, и к проверочному набору

MatLab калибровка ДМ экономическая информатика визуальные среды - 4GL Теория и практика обработки информации

Знаете ли Вы, что знаковое моделирование - это процесс построения модели с использованием специальных знаков, символов на основе общих физических закономерностей.

НОВОСТИ ФОРУМА

Рыцари теории эфира