© 2008 Алексей Померанцев
В обратной калибровке основное уравнение имеет вид (10)
Y = XB
в котором. искомая величина Y (концентрация) прямо выражается через известную матрицу спектров X. Хотя такое представление калибровочного уравнения и противоречит основному соотношению (14), такой подход обеспечивает лучшее качество моделирования.
Простейшим вариантом обратной калибровки является множественная линейная регрессия (MLR). В разделе 1.7 мы уже обсуждали свойства MLR в связи с проблемой мультиколлинеарности. В частности отмечалось, что во множественной регрессии число переменных должно быть меньше числа образцов. В нашем модельном примере число калибровочных образцов равно 9, поэтому для использования MLR необходимо отобрать из 101 канала только 8 и по ним строить калибровку. Больше переменных взять нельзя, но можно меньше. На листе MLR есть активный элемент, с помощью которого можно быстро сменить первый канал; остальные изменятся автоматически.
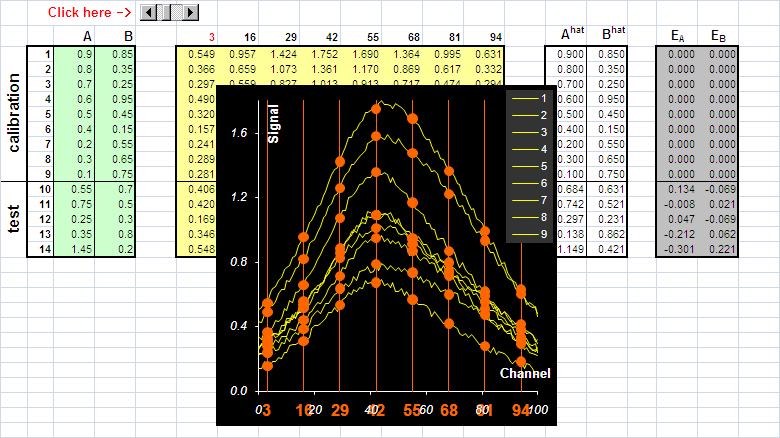
Рис.22 Множественная линейная калибровка
На Рис. 22 показано как отбираются эти каналы – равномерно, с шагом 13. Первый канал можно выбрать произвольно: от 0 до 9, тогда все последующие определяются однозначно. В результате этого отбора получается матрица независимых переменных X размерностью (14×8), состоящая из двух частей: обучающего набора (9×8) и проверочного (5×8). Используя обучающий набор переменных можно построить множественную регрессию: (10) между X и Y. Для этого можно применить формулы (11) и (12), но проще воспользоваться функцией Excel ТЕНДЕНЦИЯ.
Рис.23 Графики "измерено-предсказано" для множественной калибровки. Обучающий (a) и проверочный (b) наборы
На Рис. 23 показаны графики "измерено-предсказано" для множественной калибровки. Видно, что обучающий набор "слишком хорошо" описывается моделью. А вот проверка неудовлетворительна. Здесь заметно, и смещение, и малая корреляция.
В Табл. 4 приведены характеристики качества множественной калибровки веществ A и B, вычисленные в соответствие с формулами раздела 1.4.
Табл. 4 Характеристики качества множественной линейной калибровки
Видно, что в этом случае мы получили типичную переоценку модели (см. раздел 1.6) – число отобранных переменных слишком велико. Попытки сменить набор переменных ситуацию не улучшают. Таким образом множественная калибровка является неприемлемым методом. Она приводит к переоценке модели и дает неудовлетворительные результаты при использовании на новом (проверочном) наборе образцов.
Как мы только что видели множественная линейная калибровка неудовлетворительна – она представляет явный пример переоценки. В этом разделе мы рассмотрим пошаговую калибровку (stepwise regression, SWR), в которой отбор переменных является способом справится с переоценкой. Идея метода состоит в следующем.
Пусть имеется калибровочная модель, построенная по M отобранным каналам. Добавим к ним еще один M+1-ый канал. Выбор этого дополнительного канала основан на простом принципе – добавляется тот, который дает минимум величины RMSEC. Добавление новых каналов продолжается до тех пор, пока не наступает риск переоценки, т.е. до начала роста величины RMSEP (см. раздел 1.6).
Рис.24 Пошаговая калибровка
Очевидно, что наилучший результат для веществ A и B достигается для разных каналов. Поэтому "оптимальные" наборы для A и B отличаются. Для A – это каналы 24, 86, 11, 30, …, а для B – это каналы 100, 10, 95, 39,57, Именно в таком порядке каналы добавляются в соответствующие наборы. Отбор этих каналов – простая, но трудоемкая процедура, которую можно упростить, написав небольшой макрос в Excel.
В пошаговой регрессии существует много способов отбора "оптимальных" переменных. Тот, который использован здесь, самый простой – выбирать тот канал, на котором достигается минимум среднеквадратичной ошибки в обучении, RMSEC.
Рис.25 Среднеквадратичные остатки обучения (RMSEC) и проверки (RMSEP) в пошаговой калибровке
На Рис. 25 показано, как изменяются среднеквадратичные остатки в обучении (RMSEC) и в проверке (RMSEP) при увеличении числа каналов в SWR. В соответствие с принципом минимума RMSEP, оптимальное число каналов для вещества B – три. Это четко видно на графике. А вот выбор числа каналов для вещества A затруднителен. На соответствующем графике кривая RMSEP не имеет минимума. Так часто случается при анализе сложных данных. В рассматриваемом примере оптимальные каналы для вещества A располагаются по краям "спектральной" области – там, где влияние скрытой примеси C не существенно. Сравните Рис. 11 и Рис. 24. Поэтому SWR калибровка для вещества A никак не может "заметить" наличие вещества C. В таком сомнительном случае следует выбирать точку излома на графике RMSEP. Именно поэтому мы выбираем только два канала для вещества A.
Рис.26 Графики "измерено-предсказано" для пошаговой калибровки. Обучающий и проверочный наборы
На Рис. 26 показаны графики "измерено-предсказано" для пошаговой калибровки. Здесь заметно, что описание сбалансировано уже гораздо лучше – отличие точности обучения от проверки не так существенно, как во множественной калибровке. В Табл. 5 приведены характеристики пошаговой калибровки веществ A и B, вычисленные в соответствие с формулами раздела 1.4.
Табл. 5 Характеристики качества пошаговой калибровки
Подводя итог можно заметить, что пошаговая регрессия дала наилучший результат среди всех исследованных нами методов калибровки. Но есть и более точные методы.
|
|