|
(15) |
© 2008 Алексей Померанцев
В методе пошаговой калибровки использовались только два или три (наиболее информативных) канала из 101, и это позволило достичь приемлемого результата. Прочие каналы были отброшены как "излишние", не нужные. Такой подход представляется несколько расточительным – ведь отброшенные данные содержали полезную информацию, которую хорошо было бы использовать. В частности, применяя SWR, мы не заметили присутствие третьего вещества – примеси C, которая сильно проявляется как раз в этих исключенных каналах. Проблема, которую мы сейчас будет исследовать, состоит в следующем. Как использовать все имеющиеся данные (каналы), и, в то же время, избежать переоценки и мультколлинеарности, неизбежных при большом числе регрессионных переменных.
Решение этой дилеммы было предложено К. Пирсоном (Karl Pearson) в 1901 году – надо использовать новые, латентные переменные ta, (a=1,…A), являющиеся линейной комбинацией исходных переменных xj (j=1,…J) –
ta=pa1x1+… paJxJ
или в матричном виде
В этом уравнении T называется матрицей счетов (scores). Ее размерность – (I×A). Матрица P называется матрицей нагрузок (loadings). Ее размерность (A×J). E – это матрицей остатков, размерностью (I×J).
Новые латентные переменные ta называются главными компонентами (Principal Components), поэтому и сам метод называется методом главных компонент (PCA). Число столбцов – ta в матрице T, и pa в матрице P – равно эффективному (химическому) рангу матрицы X. Эта величина обозначается A называется числом главных компонент (PC). Она заведомо меньше числа переменных J и числа образцов I.
Для иллюстрации метода PCA, мы опять вернемся к тому, как строились модельные данные (раздел 2.4). Матрица спектров смесей X равна произведению матрицы концентраций C и матрицы спектров чистых компонентов S – формула (13). Число строк в матрице X равно числу образцов (I), и каждая ее строка соответствует спектру одного образца, снятому для J длин волн. Число строк в матрице C также равно I, а вот число столбцов соответствует числу компонентов в смеси (A=3). У матрицы чистых спектров S число строк равно числу каналов (длин волн) J, а число столбцов равно A. При анализе экспериментальных данных X, отягощенных погрешностями, представленными в формуле (13) матрицей E, эффективный ранг A может не совпадать с реальным числом компонентов в смеси.
Метод главных компонент часто применяется при исследовательском анализе химических данных. В общем случае матрицы счетов T и нагрузок P уже нельзя интерпретировать как спектры и концентрации, а число главных компонент A – как число химических компонентов, присутствующих в исследуемой системе. Тем не менее, даже формальный анализ счетов и нагрузок оказывается очень полезным для понимания устройства данных. Дадим простейшую двумерную иллюстрацию метода PCA.
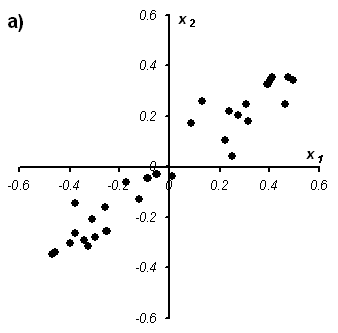
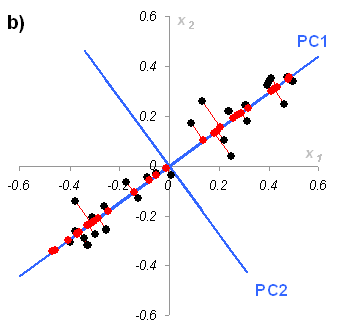
Рис.27
Графическая иллюстрация метода главных
компонент.
а) данные в исходных координатах, b)
данные в координатах главных компонент
На Рис. 27 показаны данные, состоящие только из двух переменных x1 и x2, которые связаны сильной корреляцией. На соседнем рисунке те же данные представлены в новых координатах. Вектор нагрузок p1 первой главной компоненты (PC1) определяет направление новой оси, вдоль которой происходит наибольшее изменение данных. Проекции всех исходных точек на эту ось составляют вектор t1. Вторая главная компонента p2 ортогональна первой, и ее направление (PC2) соответствует наибольшему изменению в остатках, показанных отрезками, перпендикулярными оси p1. Этот тривиальный пример показывает, что метод главных компонент осуществляется последовательно, шаг за шагом. На каждом шаге исследуются остатки Ea, среди них выбирается направление наибольшего изменения, данные проецируются на эту ось, вычисляются новые остатки, и т. д. Этот алгоритм называется NIPALS.
Метод главных компонент можно трактовать как проецирование данных на подпространство меньшей размерности A. Возникающие при этом остатки E рассматриваются как шум, не содержащий значимой химической информации. На Рис. 28 представлена графическая иллюстрация этого тезиса.
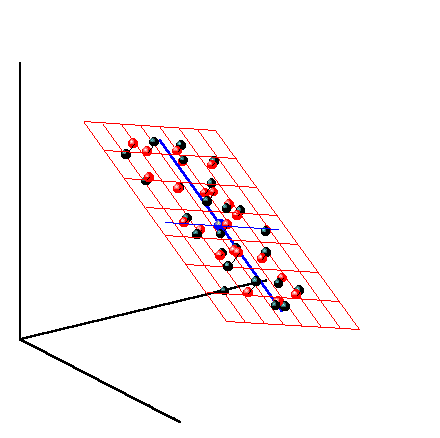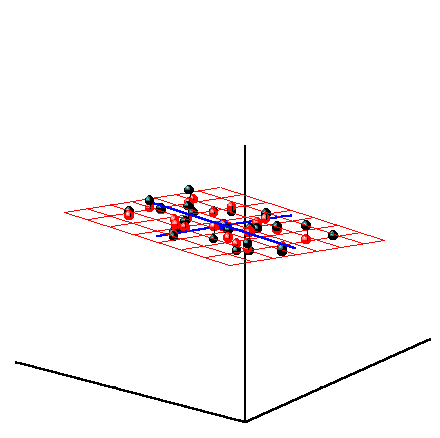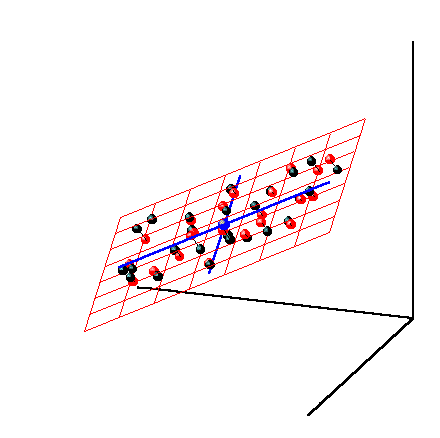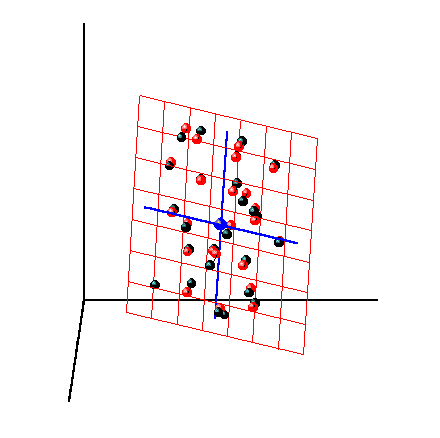
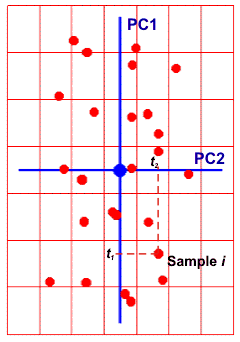
Рис.28 Метод главных компонент – как проекция на подпространство
В случае, когда метод главных компонент применяется для решения калибровочной (регрессионной) задачи он носит название регрессии на главные компоненты (Principal Component Regression, PCR).
В методе PCA проекция строится только по данным X. Значения откликов Y никак не используются. Обобщением метода PCA является метод проекций на латентные структуры (Projection on Latent Structures, PLS), который сейчас является самым популярным методом многомерной калибровки. Он во многом похож на метод PCR, с тем существенным отличием, что в PLS проводится одновременная декомпозиция матриц X и Y
Проекция строится согласованно – так, чтобы максимизировать корреляцию между соответствующими векторами X-счетов ta и Y-счетов ua. Поэтому PLS декомпозиция гораздо лучше описывает сложные связи, используя при этом меньшее число главных компонент.
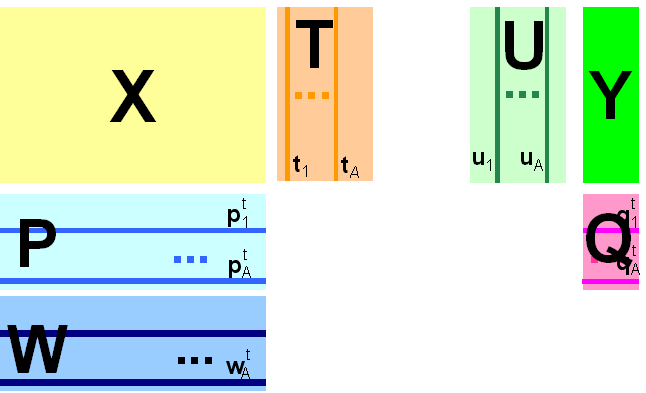
Рис. 29 Графическое представление метода проекций на латентные структуры
В том случае, когда имеется несколько откликов Y (т.е. K>1), можно построить две проекции исходных данных – PLS1 и PLS2. В первом случае для каждого из откликов yk строится свое проекционное подпространство. При этом и счета T (U) и нагрузки P (W, Q) , зависят от того, какой отклик используется. Этот подход называется PLS1. Для метода PLS2 строится одно общее проекционное пространство, которое является общим для всех откликов.
Следует обратить внимание на то, что и PCA, и PLS методы не учитывают свободного члена при разложении матрицы X. Это видно из формул (15) и (16). Исходно предполагается, что все столбцы матриц X и Y имеют нулевое среднее, т.е.,
и
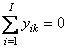для всех j=1,…, J и k=1,…, K
Этого легко можно достичь,
проведя центрирование данных (раздел
1.8 и раздел 2.5). Но, построив
калибровочную модель на центрированных
данных, надо не забыть пересчитать
полученные оценки
,
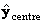добавив к ним вектор средних значений.
Приведем некоторые полезные формулы, доказательство которых можно найти во многих учебниках по анализу многомерных данных.
Во всех методах –
В методе PCR –
В методе PLS –
После того, как данные X спроецированы на подпространство размерности A, исходная калибровочная задача (10) превращается в серию регрессий на латентных переменных T –
Здесь индекс k нумерует отклики в матрице Y. Заметим, что в методах PCR и PLS2 имеется только одна матрица латентных переменных T=T1 = …= TK. Векторы bk – это неизвестные коэффициенты, а Tk – матрицы счетов. Их общая размерность A существенно меньше числа переменных J, поэтому матрица TktTk обращается устойчиво и проблема мультиколлинеарности (раздел 1.7) не существенна. Но вот другая трудность – возможность переоценки (раздел 1.6) остается, и с ней нужно уметь справляться.
Для проекционных методов сложность модели целиком определяется числом главных компонент A и выбор этой величины является основной трудностью в проекционных методах. Существует много методов определения величины A – эффективной размерности многомерных данных. Выше мы уже отмечали, что часто она связана с химическим рангом системы, т.е. с числом веществ, присутствующих в системе. Однако самым универсальным способом оценки размерности A является исследование графиков величин RMSEC и RMSEP, так как это было уже сделано в разделах 1.6 и 4.2.
Рис. 30 Графики T счетов в методе PCR
При построении многомерных калибровок, большое внимание уделяется графикам счетов и нагрузок. Они несут в себе информацию, полезную для понимания того, как устроены данные. На графике счетов (Рис. 30) каждый образец изображается в координатах (ti, tj), чаще всего – (t1, t2). Близость двух точек означает их схожесть. Образцы, расположенные близко к началу координат (например, образцы 5, 11), являются самыми типичными – образцовыми. Напротив, образцы, которые находятся далеко (например, образцы 1 и 14), являются подозрительными маргиналами, и, может быть, даже выбросами.
Рис. 31 Графики P нагрузок в методе PCR
Если график счетов используется для анализа взаимоотношений образцов, то график нагрузок применяется для исследования роли переменных. На Рис. 31 показано как меняются нагрузки в зависимости от номера канала j. Можно обратить внимание на следующую закономерность. Чем больше номер главной компоненты, тем более зашумленным выглядит соответствующий нагрузки. График первой компоненты почти гладкий. По форме он похож на спектры чистых веществ A и B (см. Рис. 11). Вторая и третья главные компоненты отличаются более сложной формой, но они все еще имеют некоторые систематические тренды. А вот четвертая и пятые компоненты представляют просто случайный шум. Так, исследуя графики нагрузок, можно установить, что в нашем примере нужно использовать только 2 или 3 главные компоненты, но ни никак не больше трех.
Калибровка на латентных переменных обычно строится на центрированном обучающем наборе (Xc, Yc). Для того, чтобы получить прогноза на проверочный или новый набор образцов (Xt, Yt), их надо также сцентрировать и спроецировать на уже имеющееся подпространство. Иными словами, нужно найти счета Tt новых образцов. В методе PCR это делается очень просто –
Tt=Xt P,
где P – это матрица нагрузок, построенная по обучающему набору.
Для методов PLS дело обстоит гораздо сложнее. Вычислительные аспекты многомерной калибровки выходят за пределы настоящего пособия. Подробное изложение всех необходимых алгоритмов, а также соответствующие MatLab коды для PCA, PLS1 и PLS2 приведены в пособии MatLab. Руководство для начинающих.
Для работы с проекционными методами существуют большие коммерческие программы, например, The Unscrambler, Simca-P, которые представляют специальную среду для проведения различных манипуляций с многомерными данными. В частности, в них реализованы и все обсуждаемые методы калибровки. Среди свободно распространяемых программ можно отметить Multivariate Analysis Add-in – надстройка для Excel, разработанная в Хемометрическом центре Бристольского университета под руководством проф. Р. Бреретона.
В этом пособии все проекционные вычисления (PCA/PLS) проводятся в рабочей книге Calibration.xls с помощью специальной надстройки (Add-In) к программе Excel, которое называется Chemometrics.xla. Оно дополняет список стандартных функций Excel и позволяет проводить разложение на листах рабочей книги. От том как ее установить написано в пособии Инсталляция Chemometrics Add-In, а о том как ее использовать, рассказано в пособии Проекционные методы в системе Excel.
Рассмотрим, как применяется PCR в модельном примере. Все вычисления приведены на листе PCR.
Сначала, по обучающим данным Xc, находится матрица PCA счетов Tс размерностью (9×5). Она состоит из пяти столбцов – главных компонент ta, a=1, 2, …, 5. С регрессионной точки зрения Tс – это матрица предикторов, т.е. независимых переменных. Двумя откликами будут центрированные значения концентраций веществ A и B. Затем, с помощью функции ТЕНДЕНЦИЯ (TREND) для каждого отклика строятся по пять регрессий. В этих регрессиях участвуют, соответственно, одна, две, ... , пять главных PCA компонент. Так строится PCR калибровка на обучающем наборе.
В этих простых вычислениях есть одна тонкость. Регрессия строится на центрированных данных Ac и Bc только потому, что в версии Excel 2003 имеется критическая ошибка, исправленная в последующих версия, начиная с Excel 2007.
Проверочные данные тоже проецируются на пространство главных компонент и для них тоже определяются PCA счета t1, …, t5. К этим счетам применяется построенная калибровка, и находятся оценки центрированных концентраций Achat. Окончательные оценки откликов Ahat для каждого числа главных компонент a получаются после учета центрирования по концентрациям
Соответствующие значения среднеквадратичных остатков обучения (RMSEC) и проверки (RMSEP) показаны на Рис. 32.
Рис. 32 Среднеквадратичные остатки обучения (RMSEC) и проверки (RMSEP) в регрессии на главные компоненты
Из Рис. 32 видно, что для обоих веществ минимум RMSEP достигается для трех PC (A=3). Таким образом, применив PCR, мы легко смогли установить, что в исследуемой системе присутствуют не два, а три вещества.
Рис. 33 Полная (TRV) и объясненная (ERV) дисперсии остатков в регрессии на главные компоненты
На Рис. 33 показаны полная (TRV) и объясненная (ERV) дисперсии остатков. Эти графики также свидетельствуют о том, что эффективная размерность системы – три. Для трех PC объясненная дисперсия практически равна 1, а полная дисперсия близка к нулю. В тоже время, видно, что графики среднеквадратичных остатков (Рис. 32) по сравнению с графиками дисперсий (Рис. 33) более наглядны.
Рис. 34 Графики "измерено-предсказано"
в регрессии на главные компоненты.
Обучающий и проверочный наборы
На Рис. 34 показаны графики "измерено-предсказано" для PCR при трех главных компонентах. Результат выглядит просто идеально – высокие коэффициенты корреляции, малые сдвиги, как в обучающем, так и проверочном наборах. Сравнивая эти графики с их аналогами в других метода – Рис. 16, Рис. 19, Рис. 21, Рис. 23, Рис. 26 – можно увидеть очевидные преимущества регрессии на главные компоненты.
В Табл. 6 приведены характеристики качества калибровки веществ A и B, построенной методом главных компонент. Все эти значения были вычислены в соответствие с формулами раздела 1.4.
Табл. 6 Характеристики качества регрессии на главные компоненты
Таким образом, мы получили, что регрессия на главные компоненты (PCR) имеет явные преимущества в сравнении с методами классической калибровки. Этот способ моделирования точнее, имеет меньшее смещение. Это объясняется тем, что в многомерной калибровке используются все имеющиеся экспериментальные данные. При этом они модифицированы так, чтобы избежать как мультиколлинеарности, так и переоценки.
Регрессия на латентные структуры (PLS1) очень похожа на метод PCR.
Отличие состоит в том, что при построении проекционного пространства учитываются не только значения предикторов X, но и откликов Y. В результате получается не одна, а две матрицы T счетов – для каждого отклика (A и B) в отдельности.
Рис. 35 Графики T счетов в методе PLS1
На Рис. 35 показаны графики первых двух T счетов в регрессии PLS1 для откликов A и B. При кажущемся различии, они очень схожи между собой и с аналогичным графиком PC1–PC2 на Рис. 30. Чтобы это понять, достаточно изменить знаки у первой главной PLS компоненты для отклика A. Такое преобразование главных компонент вполне законно. Дело в том, что, и PCA, и PLS декомпозиции определяются неоднозначно. В эти разложения всегда можно вставить произвольную, дополнительную матрицу O, такую, что OOt=I. Действительно –
X = TPt = TIPt = T (OOt) Pt = (TO) (PO)t = (Tnew) (Pnew)t.
Рис. 36. Графики весовых нагрузок W для отклика A в методе PLS1
Аналогичная картина наблюдается и для нагрузок. На Рис. 36 показаны весовые нагрузки W для отклика A. Мы используем весовые нагрузки W, а не просто нагрузки P, потому, что они, по своей сути, ближе к P нагрузкам в методе PCA.
Калибровка по методу PLS1 строится вполне аналогично методу PCR, только в этом случае для каждого отклика используется своя матрица счетов.
Рис. 37 Среднеквадратичные остатки обучения (RMSEC) и проверки (RMSEP) в регрессии PLS1
На Рис. 37 показаны среднеквадратичные остатки обучения (RMSEC) и проверки (RMSEP) в регрессии PLS1. Этот график похож на свой аналог в методе PCR (Рис. 32). Здесь тоже очевидно, что минимум RMSEP достигается для трех PC (A=3). Некоторое отличие можно заметить только в поведении RMSEC – график не выходит на предел при трех PC, а продолжает падать с ростом числа компонент. В этом проявляется особенность метода проекций на латентные структуры – нацеленность на поддержание максимальной корреляции между T и U счетами.
Рис. 38 Графики "измерено-предсказано" в PLS1 регрессии. Обучающий и проверочный наборы
Естественно, что и графики "измерено-предсказано" для калибровки методом PLS1 (Рис. 38) похожи на аналогичные графики для метода PCR (Рис. 34). То же можно сказать и о характеристиках качества калибровок, построенных методом PLS1, которые приведенные в Табл. 7.
Табл. 7 Характеристики качества PLS1 регрессии
Таким образом, калибровка методом PLS1 для рассматриваемого модельного примера очень близка по своим свойствам к калибровке методом RCR.
Если метод PLS1 был похож на метод PCR, то отличие между PLS1 и PLS2 в нашем примере еще менее заметно.
При построении проекционного пространства PLS2 также учитываются значения и X, и Y. Однако все отклики Y рассматриваются совместно, поэтому получаются не несколько (как в PLS1), а одно общее проекционное подпространство (как в PCR) В результате мы имеем пару матриц счетов T и U, и три матрицы нагрузок P, W и Q.
Рис. 39 Графики T счетов в методе PLS2
На Рис. 39 показаны графики первых трех T счетов в регрессии PLS2. Сравнивая их с аналогичными графиками на Рис. 30 и Рис. 35, легко заметить сходство. То же самое видно и для W нагрузок, представленных на Рис. 40.
Рис. 40. Графики весовых нагрузок W в методе PLS2
Сравнивая P нагрузки в методе PCR на Рис. 31 и W нагрузки в методе PLS2, можно заметить, что между первыми тремя компонентами (нагрузками) есть хорошая линейная корреляция – для PC1 положительная (R = 0.9999), а для PC2 и PC3 отрицательная (R = –0.990, R = –0.987). Но вот четвертые компоненты уже никак не связаны друг с другом (R = 0.221). Смотри Рис. 41a). Это еще одно, дополнительное подтверждение того, что эффективная размерность исследуемой системы – три.
Рис. 41 a) Корреляция между P
нагрузками в методе PCR и W нагрузками в
методе PLS2
b) Корреляция между W нагрузками вещества
B в методе PLS1 и W нагрузками в методе
PLS2
Однако между методами PLS1 и PLS2 такой интересной связи не наблюдается. На Рис. 41b) показано, как связаны между собой W нагрузки, найденные методами PLS1 и PLS2. В первом случае использовались PLS1 W нагрузки для вещества B, но и для вещества A наблюдается аналогичная картина.
После того, как построена проекция на PLS2 подпространство, калибровка строится также как в методе PCR.
Рис. 42 Среднеквадратичные остатки обучения (RMSEC) и проверки (RMSEP) в методе PLS2
По Рис. 42, на котором показаны среднеквадратичные остатки обучения (RMSEC) и проверки (RMSEP) в регрессии PLS2, легко определить нужное число главных компонент A=3. Отличия от аналогичного графика на Рис. 37 в методе PLS1 глазом не различимы.
Рис. 43 Графики "измерено-предсказано" в PLS2 регрессии. Обучающий и проверочный наборы
Также неотличимы и графики "измерено-предсказано" для PLS1 (Рис. 38) и PLS2 (Рис. 43). Характеристики качества PLS2 калибровки, которые приведены в Табл. 8 совпадают с аналогичными для PLS1 (Табл. 7).
Табл. 8 Характеристики качества PLS2 регрессии
Может сложиться впечатление, что PLS2 регрессия не дает ничего нового по сравнению с PLS1 регрессией. Действительно, в большинстве случаев так и происходит. Более того, если между откликами в матрице Y нет корреляции, то PLS1 обычно дает лучшие результаты, нежели PLS2. Для прояснения этой ситуации бывает полезно построить PCA декомпозицию для матрицы Y. Если это разложение обнаруживает связи между откликами, то метод PLS2 может оказаться очень полезным. Дальнейшее обсуждение этой интересной проблемы выходит за рамки настоящего пособия.
|
|
 |
