2. Модельные данные
2.1. Принцип линейности
Для иллюстрации и сравнения различных методов калибровки будем использовать модельный пример, в котором "экспериментальные" данные мы создадим сами. Прообразом для этого примера служит популярная задача анализа спектральных данных. Известно, что в таких экспериментах хорошо выполняется принцип линейности. Пусть имеются два вещества A и B, смешанные в концентрациях cA и cB. Тогда спектр смеси есть –
X = cA·SA+ cB·SB,
где SA и SB – спектры чистых веществ. Заметим, что тот же принцип линейности выполняется и в хроматографии, где в роли "спектров" выступают хроматографические профили чистых компонент смеси.
2.2. "Чистые" спектры
Для моделирования "чистых" спектров S(λ) мы использовали гауссовы пики –
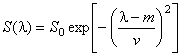 ,
,
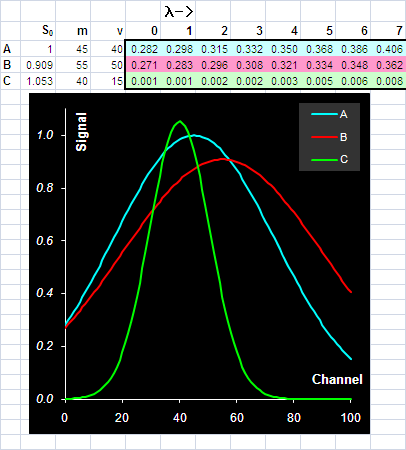
где S0, m, v – это параметры спектров, а λ = 0, 1, 2, …, 100 – это условный номер канала (длина волны, время удерживания, и т.п.). На Рис. 11 показаны спектры трех веществ: A, B и C, которые участвуют в примере. Вещества A и B – это искомые величины (отклики), а компонент C добавлен в систему как шум, т.е. нежелательная примесь.
Рис.11 Чистые спектры
Видно, что спектры сильно перекрываются, особенно A и B, у которых нет участков, где бы присутствовал только один сигнал. Это обстоятельство сильно мешает построению калибровок классическими способами.
Чистые спектры можно изменить, задавая новые величины в ячейках B4:D6, которые соответствуют параметрам формы гауссовых пиков. Например "растащить" спектры A и B так чтобы они мало перекрывались и посмотреть, что из этого получится.
2.3."Стандартные" образцы
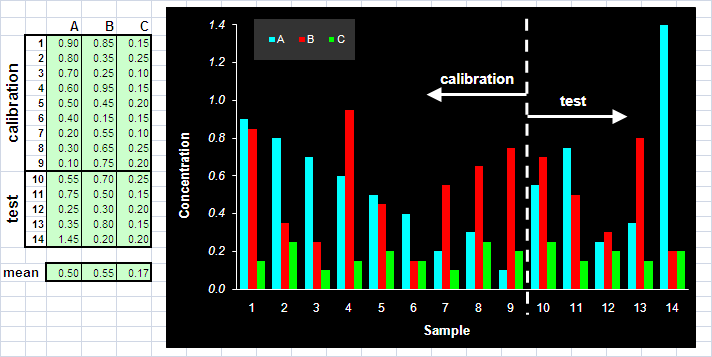
Для создания модельных данных мы должны задать концентрации всех компонентов в системе для различных образцов. Будем считать, что у нас имеется 14 образцов, из которых девять – это обучающий набор, а пять – это проверочный набор. Значения концентраций представлены на Рис. 12.
Рис.12 Концентрации в обучающем и проверочном наборах
Заметим, что среди этих образцов нет ни одного "чистого", т.е. такого в котором все концентрации, кроме одной (например, A) , равны нулю. Это тоже "мешает" использованию традиционных методов калибровки.
2.4. Создание X данных
Для получения "экспериментальных спектров" надо матрицу концентраций C умножить на матрицу чистых спектров S и добавить к результату случайные ошибки (погрешности) –
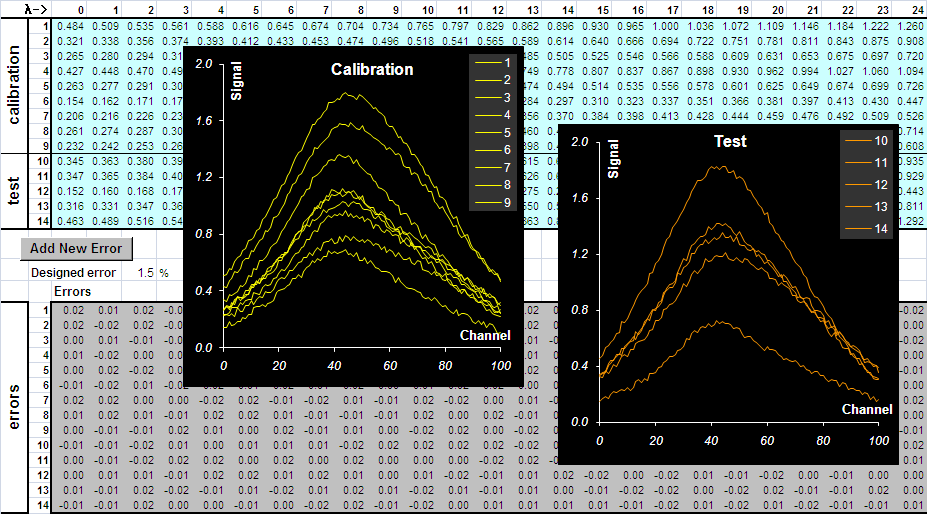
На Рис. 13 представлены полученные спектры в обучающем и проверочном наборах. Погрешности моделировались со стандартным отклонением 0.015.
Рис.13 Создание модельных данных
Генерация случайных ошибок производится с помощью простого VBA макроса , который запускается кнопкой Add New Error. Величина желаемой погрешности (СКО) предварительно задается в ячейке E18 с именем RMSE, озаглавленной Designed error. Погрешность, которая получилась в результате генерации случайных чисел выводится в ячейку J18, озаглавленную Obtained error.
Генерируя новые данные можно узнать много интересного о методах калибровки.
2.5. Центрирование данных
В соответствие с концепцией, изложенной в разделе 1.8, данные нужно правильно подготовить. В рассматриваемом модельном примере нет необходимости в выравнивании переменных – все спектральные каналы имеют схожие величины сигналов. А вот центрирование, как спектров X, так и откликов Y , бывает необходимо для построения некоторых моделей.
Для центрирования концентраций Y вычисляются средние по обучающему набору. Эти средние затем вычитаются из всех значений Y. Аналогично проводится и центрирование в данных X – вычисляются средние значения для каждого канала по обучающему набору и затем эти значения вычитаются из всех величин X – по столбцам.
2.6. Обзор данных
Итак, мы построили модельные данные (Y, X): концентрации – матрицу Y размером (14×2) и спектры – матрицу X размером (14×101). Исследуя эти данные, мы "забудем" (т.е. не будем использовать в расчетах) то, что в системе присутствует еще одно "скрытое" вещество C. Интересно, сможем ли мы обнаружить его присутствие? Кроме того, не будут использоваться и спектры чистых веществ A и B, примененные для построения данных. Мы постараемся их восстановить и сравнить с исходными спектрами.
Все данные мы разделили на два блока: обучающий (или калибровочный) – 9 образцов, и проверочный (или тестовый) – 5 образцов. Мы будем строить калибровки с помощью разных методов, используя только первый, обучающий набор. Второй, проверочный набор послужит для оценки качества получаемых моделей.
Данные используются для иллюстрации и сравнения различных методов калибровки. Они размещены в рабочей книге Excel с именем Calibration.xls.Эта книга включает в себя следующие листы:
Intro: краткое введение
Layout: схемы, объясняющая имена массивов, используемых в примере
Gun: иллюстрация пере - и недооценки в калибровке
Multicollinearity: иллюстрация проблемы мультиколлинеарности в калибровке
Pure Spectra: истинные чистые спектры S
Concentrations: истинные концентрационные профили C
Data: модельные данные, используемые в примере..
UVR: одноканальная калибровка
Vierordt: калибровка методом Фирордта
Indirect: непрямая калибровка
MLR: множественная линейная регрессия
SWR: калибровка пошаговой реегрессией
PCR: регрессия на главные компоненты
PLS1: метод проекция на латентные переменные 1
PLS2: метод проекция на латентные переменные 2
Compare сравнение различных методов
|
|