© 2008 Алексей Померанцев
Классическая калибровка опирается на использовании того же принципа линейности, по которому строились модельные данные, т.е. на уравнение (13)
Здесь X=Xc и C=Yc – это обучающая часть исходных данных (не центрированных), а S – это матрица "чистых спектров" (она же матрица чувствительности).
Если матрица S известна априори, то концентрации определяются так
|
C=XS+ |
|
где S+ = =St(SSt)−1– это псевдообратная матрица. Этот случай называется прямой калибровкой. Однако, на практике матрица чистых спектров, как правило, неизвестна и ее приходится восстанавливать из обучающих данных.
Это самый простой, наивный вид калибровки. Если для каждого аналита из всех данных X выделить один канал (длину волны), то получится несколько векторов x. Тогда, используя обучающие данные, можно построить для каждого вещества простейшую одномерную регрессию –
x=sc+b ,
одну для вещества A (c=cA), а другую для B (c=cB). Формулы для оценивания коэффициентов s (наклон)и b (отсечение) можно найти в любом пособии по линейной регрессии, например, здесь. В Excel это проще всего сделать с помощью функции ЛИНЕЙН (LINEST). После того, как эти коэффициенты найдены, значения концентраций можно вычислять по уравнению
c=(x–b)/s
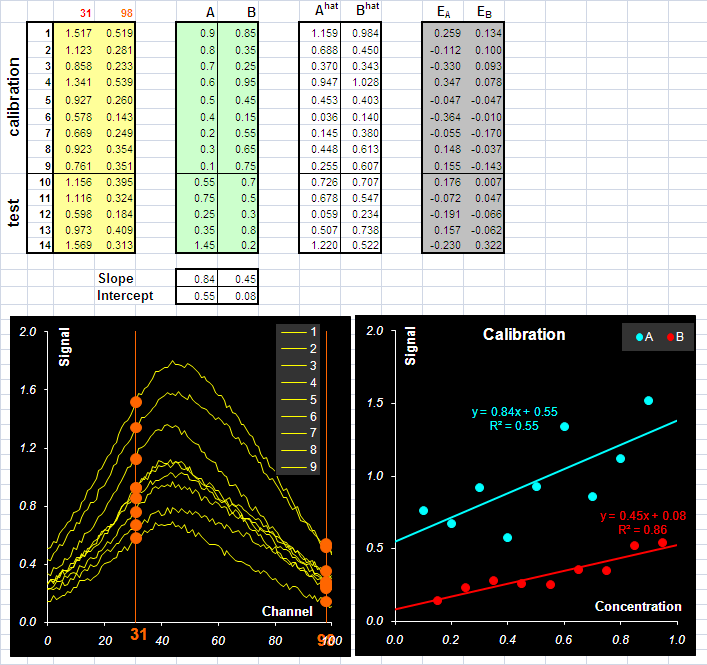
На Рис.14 приведен пример построения двух этих регрессий для каналов 31 (A) и 98 (B). График показывает, как проходят линии регрессий для веществ A и B.
Рис.14 Калибровка по одному каналу)
Обратите внимание, что в каждом калибровочном уравнении присутствует свободный член b. Это противоречит исходному уравнению (13), но зато позволяет учесть влияние фона, или, как в нашем случае, присутствие посторонней примеси (вещества C). Величины коэффициентов s (наклон) соответствуют значениям "чистых" спектров. На Рис. 15 показаны "чистые" спектры веществ A и B и соответствующие значения коэффициентов m.
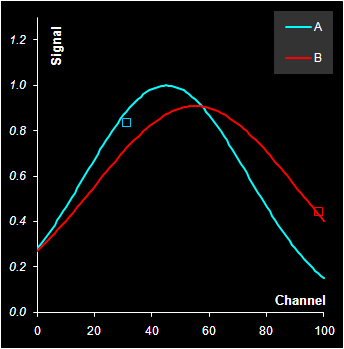
Рис.15 "Чистые" спектры и их оценки для выбранных каналов
Для визуальной оценки качества
калибровки традиционно используются
графики "измерено-предсказано", в
которых по оси абсцисс откладываются
известные (стандартные) концентрации y,
а по оси ординат соответствующие им
величины оценок
,
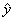найденные (предсказанные) с помощью
построенной калибровки. Такие графики
показаны на Рис. 16. Помимо
вышеупомянутых данных (точки), на таких
графиках обычно показывают линии
регрессии ky+b. Коэффициенты
k (наклон)
и b (отсечение) характеризуют "качество"
калибровки. В идеальном случае k=1 и b=0.
Чем дальше от идеала, тем хуже
калибровка. Кроме того, на таких
графиках обычно приводится значение
коэффициента корреляции R2
между y и
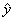
Рис.16 Графики "измерено-предсказано" для однофакторной калибровки. Обучающий и проверочный наборы
В Табл. 1 приведены характеристики качества однофакторной калибровки веществ A и B, вычисленные в соответствие с формулами раздела 1.4.
Табл. 1 Характеристики качества однофакторной калибровки
Разумеется одномерную калибровку можно проводить по любому каналу. На листе UVR для этого достаточно изменить значения в ячейках C2 и D2, которые соответствуют двум каналам – для веществ A и B. и проверить как меняется качество калибровки. Так наилучшее значение RMSEP=0.173 для вещества A достигается при калибровке по 31 каналу, а наихудшее значение RMSEP=0.702 получается при λ =97. Соответственно для вещества B имеем: наилучшее значение RMSEP=0.151 для λ =98 и наихудшее RMSEP=0.611 для λ =20.
Существует мнение, что калибровку лучше проводить в точке, где соответствующий "чистый спектр" имеет максимум. Из рассмотренного примера видно, что это не так. В точке λ =45 (максимум A) RMSEP=0.205, а в точке λ =55 (максимум B) RMSEP=0.484.
Впервые задача анализа спектрофотометрических данных была рассмотрена в работе Карла фон Фирордта (Karl von Vierordt в 1873 г. Исследуя изменения гемоглобина в крови, он предложил метод калибровки, который и теперь, спустя 140 лет, еще очень популярен у некоторых аналитиков.
Метод Фирордта похож на метод одноканальной калибровки. В нем также выбирается по одному каналу для каждого вещества, но регрессионные уравнения рассматриваются не независимо, а совместно
Здесь матрица
имеет столько
столбцов, сколько определяется веществ (у нас 2), матрица
Yc – это известные
значения концентраций в обучающем наборе (у нас 2), а матрица S – это
неизвестная квадратная ( у нас 2×2) матрица чувствительности, которую нужно
оценить. Заметим, что в традиционном методе Фирордта свободный член отсутствует
в полном согласии с уравнением (13),
Для оценки матрицы чувствительности S умножим это уравнение слева на транспонированную матрицу концентраций Yc
Тогда матрица –
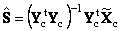
будет оценкой матрицы чувствительности.
На Рис. 17 показано применение метода Фирордта для модельного примера, где для калибровки выбраны два канала 29 и 100.
Рис.17 Применение метода Фирордта
График "предсказано-измерено" представляет результаты калибровки сигнала (спектров x) для выбранных каналов. Элементы матрицы чувствительности S соответствуют значениям матрицы "чистых" спектров. На Рис. 18 показано это соответствие.
Рис.18 Элементы матрицы чувствительности S (точки) в методе Фирордта и "чистые" спектры
Для оценки и предсказания значений концентрации веществ A и B. нужно вычислить матрицу обратную к матрице чувствительности S. Сделать это просто, т.к. эта матрица квадратная. Тогда матрица V
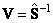
будет линейным "оценивателем"
матрицы концентраций Y. Для того,
чтобы найти оценки величин
концентраций в обучающем наборе, надо
матрицу V умножить на матрицу
соответствующих спектров
–
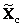Аналогично, для оценки концентраций в проверочном наборе, матрица V умножается на Xt –
Графики "предсказано-измерено" показаны на Рис. 19
Рис.19 Графики "измерено-предсказано" для метода Фирордта. Обучающий и проверочный наборы
В Табл. 2 приведены характеристики качества калибровки по методу Фирордта веществ A и B, вычисленные в соответствие с формулами раздела 1.4.
Табл. 2 Характеристики качества калибровки по методу Фирордта
Качество калибровки сильно зависит от того, какие каналы выбраны в качестве аналитических. Часто рекомендуется действовать таким образом. Строится график F(λ)= sA/sB , где sAи sB – это "чистые спектры". На нем определяют такие точки λ1 и λ2, в которых разница |F(λ1) – F(λ2)| максимальна. Способ правильный, но построить график F(λ), не зная чистых спектров, невозможно.
В методе Фирордта. для калибровки используются несколько каналов – столько, сколько веществ нужно определить. Естественно обобщить этот подход, задействовав все имеющиеся у нас обучающие данные.
Будем рассматривать полное уравнение классической калибровки
X=СS
Также как в методе Фирордта умножим его слева на транспонированную матрицу Yc
Тогда матрица –
является оценкой матрицы "чистых спектров". Заметим, что это уже не квадратная матрица – она имеет размерность A×J (В нашем примере 2×101). Сравним ее с исходной матрицей чистых спектров A и B.
На Рис. 16 показаны исходные и восстановленные спектры. Различие между ними особенно заметно в той области, где велик вклад от примеси C. На краях – там, где спектр C стремится к нулю (при λ<20 и λ>60) – спектры A и B восстановлены практически идеально. К сожалению, не подозревая о существовании в системе вещества C, мы не сможем заметить этого факта.
Рис.20 Оценка матрицы "чистых спектров" в непрямой калибровке
Продолжая построение
калибровки, положим в уравнении (14)
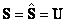и
умножим его справа на матрицу Ut
–
Тогда матрица размерностью (101×2) –
будет линейным "оценивателем" матрицы концентраций Y. Для того, чтобы найти оценки величин концентраций в обучающем наборе, надо матрицу V умножить на матрицу соответствующих спектров Xc –
Аналогично, для оценки концентраций в проверочном наборе, матрица V умножается на Xt –
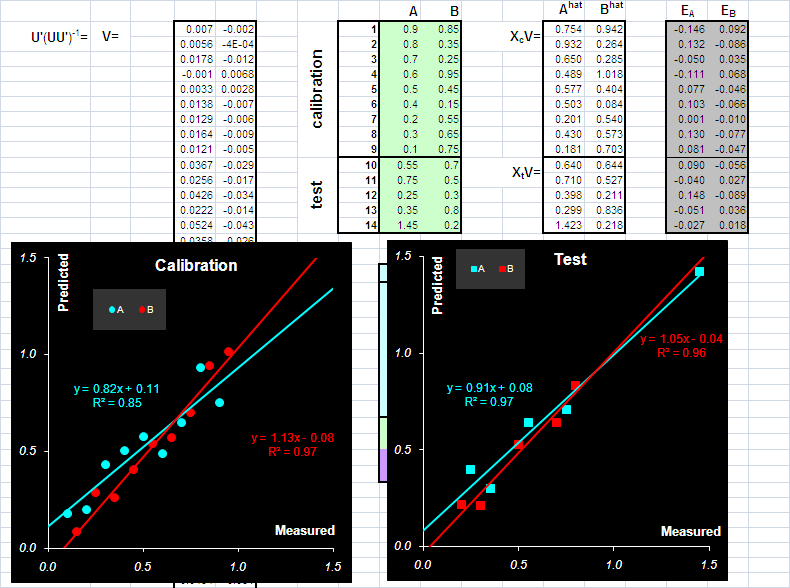
Рис.21 Оценка концентраций в непрямой калибровке
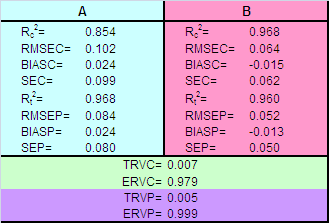
В Табл. 3 приведены различные характеристики качества прямой калибровки веществ A и B, вычисленные в соответствие с формулами раздела 1.4.
Табл. 3 Характеристики качества непрямой калибровки
Бытует устойчивое мнение, что классическая калибровка лучше обратной. Для объяснения ее преимущества говорят, что она опирается на фундаментальные физические принципы, такие как закон Ламберта-Бэра. С точки зрения математиков, все выглядит наоборот. Во-первых, сама калибровка является "обратной" по отношению к искомым величинам Y. Во-вторых, процедура, с помощью которой оцениваются отклики, является неустойчивой. Действительно, если между искомыми концентрациями A и B имеется линейная связь, например cB ~ 0.5cA, то матрица YtY не имеет обратной, или она обращается с большой ошибкой. Линейная связь между искомыми концентрациями часто наблюдается при анализе объектов окружающей среды, в которых она обусловлена естественными причинами. В-третьих, классическая калибровка не дает нам никаких признаков отклонения системы от ее идеальной модели, например, не позволяет обнаружить примеси (вещество C). Наконец, далее мы увидим, что и качество такой калибровки (точность, прецизионность) уступает многим современным методам.
|
|
 |
