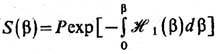
Термодинамическая теория возмущений (статистическая теория возмущений) - метод приближённого регулярного вычисления
свободной энергии (или к--л. др. термодинамич. величины) физ. системы, аналогичный
возмущений теории для энергии осн. состояния в квантовой механике.
Построение термодинамической теория возмущений в. предполагает возможность разбиения полного гамильтониана H данной
квантовой физ. системы (или соответственно Гамильтона функции для классич.
системы) на свободный (нулевой) гамильтониан H0 и гамильтониан
взаимодействия lH1, где константа
связи l может быть, вообще говоря, не мала. Согласно термодинамической теория
возмущений, свободная энергия F (см. Гельмгольца энергия)такой системы
может быть представлена в аддитивной форме F=F0 + F1, где F0, по предположению, вычисляется точно, a
F1 имеет вид бесконечного разложения (ряда) по степеням
bl, где b
= 1/kT, Т-абс. темп-pa. Очевидно, условия сходимости подобного ряда тем
лучше, чем слабее взаимодействие l и выше температура
Т, хотя строгие критерии сходимости рядов термодинамической теории возмущений в общем случае отсутствуют.
Термодинамическая теория возмущений основана на формальной
аналогии между Шрёдин-гера уравнением для волновой функции системы и Блоха
уравнением для статистич. оператора r квантового кано-нич. (или большого
канонич.) распределения Гиббса для той же системы. Ур-ние Блоха дr/дb
= - Hr с нач. условием r|b=0 = 1 получается
из ур-ния Шрёдингера формальной заменой времени t на мнимое время hb/i,
В рамках термодинамической теории возмущений решение для r, согласно Т. Мацубаре [1], ищется в виде r
= r0S(b) с нач. условием S(0)=1, где S(b) -
так наз. температурная S-м а т ри ц
а, имеющая вид, аналогичный матрице рассеяния в квантовой механике:
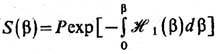
или
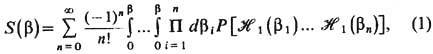
где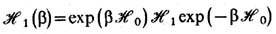 
- гамильтониан 
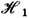в представлении взаимодействия по мнимому времени, P-оператор "хронологич."
упорядочения по мнимому времени (b1 >b2>...>
bn). Тогда для канонич. (или соответственно большой канонич.)
статистич. суммы данной системы Z = exp(-bF)имеем
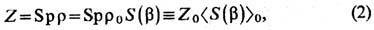
где введены обозначения
Z0 = Spr0 = exp( - bF0), <...>0=Z0-1Sp(r0
...) - термодинамич. среднее для свободной (невозмущённой) системы. Вычисление
Z существенно упрощается благодаря наличию для <S(b)>0
теоремы о разложении по так наз. связным средним (кумулянтам), приводящей
к экспоненциальной ф-ле <S(b)>0 = exp<S(b)>0,c,где
с - индекс связности. Тогда, логарифмируя (2), находим, что искомая добавка
F1 к свободной энергии F0 невозмущённой
системы имеет вид:
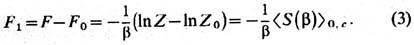
Эфф, вычисление связных
средних в каждом порядке разложения (1) для S(b) (а также частичное
суммирование к--л. подпоследовательностей членов этого разложения) проводится,
как правило, с использованием графич. техники, вполне аналогичной технике Фейнмана
диаграмм, где вместо причинных функций Грина, характерных для квантовой теории
поля, применяются так наз. мацубаровские функции Грина (см. Грина функция
в статистич. физике). В рамках термодинамической теории возмущений имеет место
теорема (Уорд и Лат-тинжер [2]) о стационарности (точнее, минимальности) функционала
свободной энергии F по отношению к вариациям полной функции Грина или массового
оператора; частный случай этой теоремы, соответствующий обобщённому среднего
поля приближению, эквивалентен так наз. статистическому вариационному
принципу H. H. Боголюбова (1956), согласно которому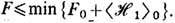 
Согласно этой теореме, для F1
может быть получено формальное замкнутое выражение в виде так наз. интеграла
по константе связи (см., напр., [4, 7]), через полную электронную функцию Грина Gl. и
соответствующий массовый оператор Мl или через полную
фононную функцию Грина Dl и соответствующий поляризац. оператор
Пl след, вида (в символич. записи):
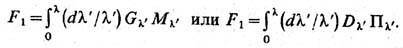
Практич. вычисление слагаемых, входящих в осн. ф-лы термодинамической
теории возмущений (1) и (3), основано обычно на записи гамильтониана
взаимодействия H1 в представлении вторичного квантования
с помощью ферми-, бозе- или паули-операторов. Соответственно при вычислениях
средних в (3) и (1) используется температурное обобщение Вика теоремы о
спариваниях, доказанное К. Блохом и Де Доминисисом [3 ] для ферми- и бозе-операторов
и С. В. Тябликовым и В. А. Москаленко [5] - для паули-операторов.
Построение термодинамической теории возмущений для классич. физ. систем существенно упрощается по сравнению с квантовыми
благодаря тому, что для коммутирующих в этом случае при любых значениях bi
сомножителей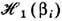 
величина S(b) превращается из хронологич. Р-экспоненты в обычную,
для к-рой кумулянты F1(n) любого
порядка вычисляются значительно проще; напр., в первом порядке по взаимодействию
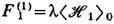, а во
втором F21 = ( - l2b/2)<(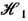
-
<
>0)2>0.
Существует обобщение термодинамической теории возмущений на случай возмущений 
,
явно зависящих от времени t (напр., при вычислении функций линейной реакции
системы на такое возмущение, а также кинетич. коэффициентов, согласно Грина-Кубо
формулам). В этом случае при построении аналога S-матрицы для неравновесного
статистич. оператора используется как мнимое, так и обычное время, так что соответствующая
диаграммная техника значительно усложняется (см., напр., Л. Каданов, Г. Бейм
[6]).
Примеры применения термодинамической теории возмущений для разл. типов физ. систем (напр., для неидеальных газов низкой плотности с короткодействием - так наз. газовое приближение или для системы частиц с дальнодействующим кулоновским взаимодействием- так наз. плазменное приближение) подробно рассмотрены в монографии [7] (см. также в ст. Вириальное разложение, Майера диаграммы в статистич. физике). Термодинамическая теория возмущений широко используется также для анализа физ. свойств систем, описываемых спиновым гамильтонианом, выше критич. точки фазового перехода; напр., для сильно магнитных систем [8 ] строятся т. н. высокотемпературные разложения для намагниченности, восприимчивости и т. п., к-рые затем анализируются методом Паде аппроксимации с целью нахождения критических показателей.
12;
Ю. Г. Рудой
Дело в том, что в его постановке и выводах произведена подмена, аналогичная подмене в школьной шуточной задачке на сообразительность, в которой спрашивается:
- Cколько яблок на березе, если на одной ветке их 5, на другой ветке - 10 и так далее
При этом внимание учеников намеренно отвлекается от того основополагающего факта, что на березе яблоки не растут, в принципе.
В эксперименте Майкельсона ставится вопрос о движении эфира относительно покоящегося в лабораторной системе интерферометра. Однако, если мы ищем эфир, как базовую материю, из которой состоит всё вещество интерферометра, лаборатории, да и Земли в целом, то, естественно, эфир тоже будет неподвижен, так как земное вещество есть всего навсего определенным образом структурированный эфир, и никак не может двигаться относительно самого себя.
Удивительно, что этот цирковой трюк овладел на 120 лет умами физиков на полном серьезе, хотя его прототипы есть в сказках-небылицах всех народов всех времен, включая барона Мюнхаузена, вытащившего себя за волосы из болота, и призванных показать детям возможные жульничества и тем защитить их во взрослой жизни. Подробнее читайте в FAQ по эфирной физике.
|
|
 |
