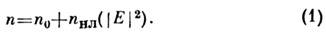
Самофокусировка света - концентрация энергии световой волны,
распространяющейся в нелинейной среде, показатель преломления п к-рой
растёт с увеличением амплитуды поля Е:
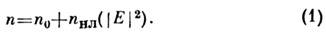
Показатель преломления среды может увеличиваться с ростом поля Е вследствие изменения нелинейной поляризации среды, оптич. Керра эффекта, электрострикции, нагрева, резонансного возбуждения среды и т. д.
Под действием светового пучка, имеющего, напр., гауссову форму, нелинейная среда становится оптически неоднородной: в центре пучка, где больше интенсивность, показатель преломления больше, чем для краёв пучка, а следовательно, фазовая скорость в центре будет меньше, чем по краям пучка. Это приведёт к искажению первоначально плоского волнового фронта, а лучи, распространяющиеся по нормали к фронту, искривляются (нелилейная рефракция) к оси (рис. 1,а). Первоначально однородная среда становится своеобразной объёмной собирающей линзой, фокус к-рой находится на нек-ром расстоянии fнл от входа пучка в среду.
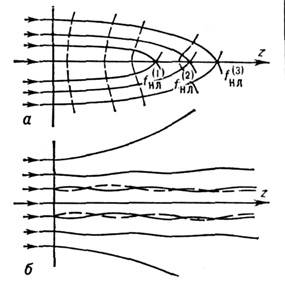
Рис. 1. Самофокусировка света в нелинейной среде: а - возникновение коллапса и многофокусировки (штриховыми линиями показан волновой фронт); б - траектория лучей в возникающем нелинейном диэлектрич. волноводе.
Явление самофокусировки света теоретически было предсказано Г. А. Аскарьяном в 1962 и впервые наблюдалось Н. П. Пилипецким и А. Р. Рустамовым в 1965.
В тонком нелинейном слое, толщина к-рого l значительно меньше
фокусного расстояния fнл, всё происходит во многом аналогично
самодефокусировке
света, только в случае фокусировки и лучи, пройдя слои, сначала сходятся в фокальной плоскости, а затем уходят
в дальнее поле. Как и при самодефокусировке, благодаря нелинейным аберрациям,
угл. распределение пучка при прохождении им самофокусирующей линзы имеет
кольцевую структуру.
и лучи, пройдя слои, сначала сходятся в фокальной плоскости, а затем уходят
в дальнее поле. Как и при самодефокусировке, благодаря нелинейным аберрациям,
угл. распределение пучка при прохождении им самофокусирующей линзы имеет
кольцевую структуру.
Если толщина нелинейного слоя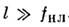 ,
самофокусировка света описывается квазиоптич. нелинейным ур-нием, в к-ром учитывается
не только нелинейная рефракция, но и дифракция:
,
самофокусировка света описывается квазиоптич. нелинейным ур-нием, в к-ром учитывается
не только нелинейная рефракция, но и дифракция:
Это параболич. ур-ние типа нелинейного ур-ния Шрёдингера имеет ряд интегралов
движения Ij, сохраняющих свои, величины в процессе распространения.
Кроме очевидного интеграла I1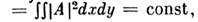
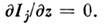 выражающего
закон сохранения энергии, существует интеграл
выражающего
закон сохранения энергии, существует интеграл

характеризующий соотношение линейной дифракции (первый член подынтегрального
выражения) и самовоздействие пучка. В слабых полях (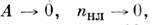
) интеграл (3) положителен и пучок испытывает только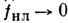 дифракцию. Однако в нелинейной среде под воздействием достаточно сильных
полей знак I3 может стать отрицательным за счёт члена
дифракцию. Однако в нелинейной среде под воздействием достаточно сильных
полей знак I3 может стать отрицательным за счёт члена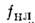 и линейная дифракция сменяется самофокусировкой или образованием нелинейного
волновода (рис. 1, б). Нелинейный волновод образуется при компенсации дифракц.
расходимости нелинейной рефракцией:
и линейная дифракция сменяется самофокусировкой или образованием нелинейного
волновода (рис. 1, б). Нелинейный волновод образуется при компенсации дифракц.
расходимости нелинейной рефракцией:
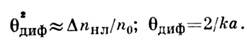
Поперечное распределение амплитуды в нелинейном волноводе можно рассчитать,
если искать решение ур-ния (2) в виде неограниченного пучка ( при
при
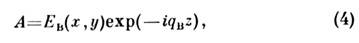
где ЕВ и qB - собств. функции и собств.
числа пространственных мод нелинейного волновода. В кубичной нелинейной
среде, когда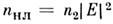 , амплитудный профиль EB описывается ур-нием, следующим
из (2):
, амплитудный профиль EB описывается ур-нием, следующим
из (2):
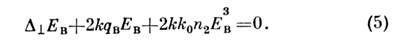
При распространении пучка в среде существует дискретный спектр нелинейных
мод, каждая из к-рых несёт свою критич. мощность, начиная с к-рой пучок
самофокусируется. Так, напр., низшая осесимметричная мода, имеющая колоколообразный
амплитудный профиль, имеет критич. мощность
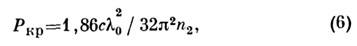
к-рая не зависит от поперечного радиуса пучка а, прямо пропорциональна
квадрату длины волны (чем меньше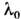 ,
тем слабее дифракционная расходимость, тем при меньшей мощности начинается
эффект самофокусировки) и обратно пропорциональна коэф. нелинейности n2.
,
тем слабее дифракционная расходимость, тем при меньшей мощности начинается
эффект самофокусировки) и обратно пропорциональна коэф. нелинейности n2.
С увеличением амплитуды поля Е0 нелинейный фокус смещается ко входу и вслед за первым фокусом возникает второй, третий и т. д. (рис. 1, а и рис. 2). Число фокусов растёт с увеличением мощности источника, возникает мяогофокусная структура. В случае мощных коротких импульсов фокусы движутся очень быстро, с околосветовой скоростью.

Рис. 2. Многофокусная самофокусировка пучка в среде с кубичной нелинейностью.
В мощных пучках с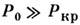 нелинейная рефракция превалирует над дифракцией и для описания поведения
пучка можно воспользоваться метопом геом. оптики, представляя в (2)
нелинейная рефракция превалирует над дифракцией и для описания поведения
пучка можно воспользоваться метопом геом. оптики, представляя в (2)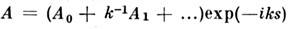
при
 . Тогда можно получить след. ур-ния:
. Тогда можно получить след. ур-ния:
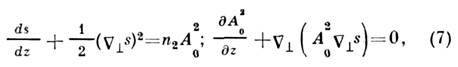
первое из к-рых - ур-ние эйконала в нелинейной среде, второе
- ур-ние переноса излучения. Величина имеет простой смысл угла наклона элементарного луча к продольной оси z.
Из (7) легко найти ур-ния для
имеет простой смысл угла наклона элементарного луча к продольной оси z.
Из (7) легко найти ур-ния для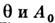 , аналогичные ур-ниям гидродинамики. Ур-ния (7) имеют простое автомодельное
решение для параболич. профиля пучка:
, аналогичные ур-ниям гидродинамики. Ур-ния (7) имеют простое автомодельное
решение для параболич. профиля пучка:
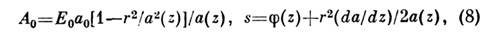
где поперечный радиус пучка уменьшается с расстоянием по закону
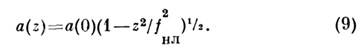
Видно, что траектории всех лучей подобны друг другу, они сходятся в
одну точку, расположенную на расстоянии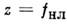 ,
,
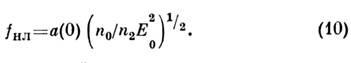
По мере приближения к фокусу лучи всё более искривляются, а поле На
оси неограниченно нарастает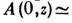
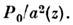 Пучок «cхлопывается» (волновой коллапс ).Это явление не устраняется
даже с учётом дифракции и нелинейных аберраций.
Пучок «cхлопывается» (волновой коллапс ).Это явление не устраняется
даже с учётом дифракции и нелинейных аберраций.
Картина нестационарной самофокусировки с учётом релаксации нелинейности
описывается ур-нием
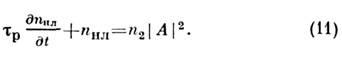
Т. к. передняя часть импульса света не участвует в самофокусировке света, она распространяется как в линейной среде, испытывая только дифракцию, а средняя и задняя части импульса, испытывая ещё и нелинейную рефракцию, самофокусируются, образуя квазиволновод (рис. 3). Поле в квазиволноводе нарастает медленнее и ограничено по величине (нет коллапса). На больших расстояниях из-за дифракционного расплывания передней части импульса длина квазиволновода сокращается вплоть до полного исчезновения.
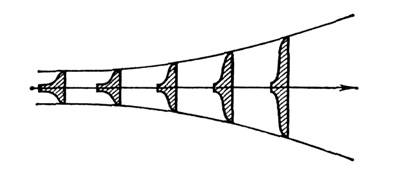
Рис. 3. Картина нестационарной самофокусировки короткого светового импульса. На переднем фронте нелинейный отклик ещё не установился и происходит линейное распространение импульса, задняя часть импульса сжимается за счёт нелинейной рефракции.
Мощный световой пучок испытывает в самофокусирующей среде модуляц. неустойчивость,
приводящую к т. н. мелкомасштабной самофокусировки света. Если в световой волне с амплитудой
Е0 появляются пространственные флуктуации р (малые возмущения амплитуды
и фазы)
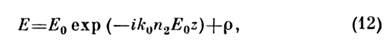
то благодаря параметрич. неустойчивости амплитуда малых возмущений экспоненциально
растёт с расстоянием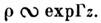 Отд. пространственные фурье-компоненты
Отд. пространственные фурье-компоненты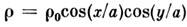 имеют разные инкременты
имеют разные инкременты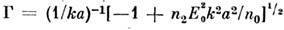 Наиб. инкремент
Наиб. инкремент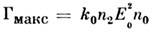 имеют возмущения с поперечным масштабом модуляции
имеют возмущения с поперечным масштабом модуляции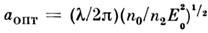 , поэтому пучок разбивается на отд. нити с радиусом аопт. В
нити с таким радиусом захватывается мощность порядка критической. В пучке
происходит конкуренция самофокусировки пучка как целого на длине
, поэтому пучок разбивается на отд. нити с радиусом аопт. В
нити с таким радиусом захватывается мощность порядка критической. В пучке
происходит конкуренция самофокусировки пучка как целого на длине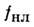
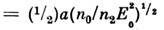 и процесса распада пучка на отд. нити за счёт дифракции. Если профиль пучка
достаточно гладкий, то мелкомасштабная структура не проявится на длине,
равной fнл.
и процесса распада пучка на отд. нити за счёт дифракции. Если профиль пучка
достаточно гладкий, то мелкомасштабная структура не проявится на длине,
равной fнл.
Самофокусировка может развиваться и на квадратичной нелинейности при
трёхволновом когерентном взаимодействии, когда частоты и волновые векторы
связаны соотношениями w1 + w2 = w3 и k1+
k2 = k3. В вырожденном по частоте случае генерация
второй оптич. гармоники с учётом дифракции описывается двумя амплитудными
ур-ниями:
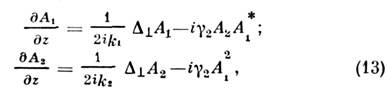
где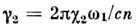 - коэф. нелинейности,
- коэф. нелинейности, - нелинейная восприимчивость 2-го порядка.
- нелинейная восприимчивость 2-го порядка.
При возбуждении гармоники независимо от знака коэф. нелинейности самофокусировка света возникает одновременно у двух пучков (рис. 4). Критич. мощность двухволновой
взаимофокусировки
самофокусировка света возникает одновременно у двух пучков (рис. 4). Критич. мощность двухволновой
взаимофокусировки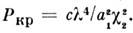
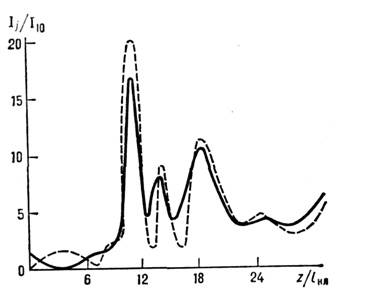
Рис. 4. Взаимофокусировка волновых пучков основной (сплошная линия) и второй (штриховая линия) гармоник в среде с квадратичной нелинейностью.
Самофокусировка света может привести к световому пробою, способствует развитию процессов вынужденного рассеяния и др. нелинейных процессов. С помощью самофокусировки света можно создавать сверхсильные световые поля.

А. П. Сухоруков
|
|