Глоссарий по физике

Нелинейные восприимчивости

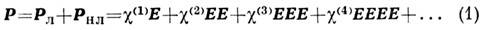
Нелинейные восприимчивости - тензорные коэффициенты, связывающие нелинейную часть поляризации Р = Р_л + Р_нл единичного объёма среды, возникающую под действием сильных электрических (в частности, световых) полей, с величинами напряжён-ностей этих полей [1,2,3]. Соответствующее соотношение, называемое материальным ур-нием, может быть записано в форме разложения по степеням напряжённости электрич. поля Е:

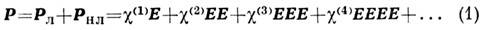
Материальное ур-ние нелинейной немагн. среды без пространств. дисперсии может быть представлено в виде

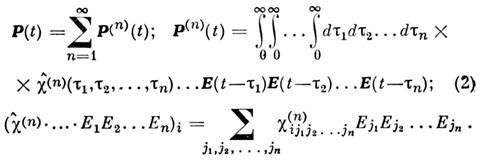
Здесь тензор c⁽ⁿ⁾ ранга (п + 1) - Н. в. n-го порядка, описывающая отклик среды на совокупность возбуждений в разл. моменты времени t - t_l, t - t₂, t - t_n. (Это разложение - сходящееся, т. е. ряд можно ограничить неск. членами, т. к. память среды на возбуждение конечна вследствие процессов диссипации.)

Для описания задач нелинейной оптики и нелинейной спектроскопии, где используются когерентные лазерные источники возбуждения, наиб. важен аналог соотношения (2), записанный в спектральном представлении для дискретного спектра возбуждения:

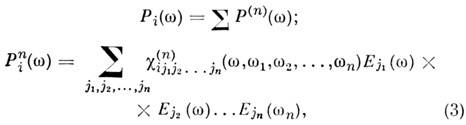
где w = w₁ + w₂ +...+ w_n - частота нелинейного отклика.

Будучи оптич. характеристиками среды, тензоры Н. в. должны обладать определ. симметрией, отражающей структурную симметрию среды [4]. В соответствии с этим нек-рые тензорные элементы оказываются равными нулю, а другие связаны друг с другом, что уменьшает число ненулевых независимых компонент. Напр., тензор кубич. Н. в. c⁽³⁾, в общем случае содержащий 81 компоненту, в изотропной среде имеет только три независимые компоненты. В средах с центром инверсии все Н. в. чётных порядков тождественно равны нулю. В средах без диссипации Н. в. любого порядка - действит. величина.

Действительная и мнимая части восприимчивости 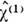описывают линейные оптич. эффекты (преломление и поглощение света). Н. в. 2-го порядка 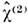, свойственная средам, не имеющим центра симметрии, описывает генерацию второй оптич. гармоники, оптич. выпрямление (см. Детектирование света)и др. процессы нелинейного смешения двух волн с частотами w₁ и w₂, приводящие к рождению излучения на суммарной или разностной частотах |w₁ b w₂|. Кубическая Н. в. 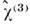, отличная от нуля в средах с симметрией любого типа, описывает разл. процессы самовоздействия света - нелинейное поглощение, самофокусировку и дефокусировку, самоиндуциров. вращение эллипса поляризации. Кубической Н. в. объясняются также процессы, возникающие при взаимодействии трёх волн с разл. частотами w₁, w₂ и w₃, приводящие к появлению излучения на комбинац. частотах w = |w₁ b w₂ b w₃|, напр. генерации третьей гармоники при вынужденном комбинац. рассеянии, вынужденном Мандельштама - Бриллюэна рассеянии и т. д. Более высокий ранг тензора 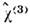по сравнению с тензором 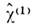проявляется в том, что кристаллы кубич. классов, изотропные с точки зрения своих линейных оптич. свойств, в нелинейной оптике анизотропны. Это приводит к поляризац. особенностям нелинейного поглощения, генерации третьей оптич. гармоники, к самоиндуциров. повороту плоскости поляризации линейно поляризованного света (см. Нелинейная оптическая активность).

Микромодели Н. в. Наиб. универсальная причина нелинейных оптич. эффектов - нелинейный отклик атомарного или молекулярного осциллятора на световое воздействие.

В классич. модели среды как совокупности заряженных ангармонич. осцилляторов удаётся вычислить смещение заряда q_i на расстояние r_i от положения равновесия под действием электрич. поля световой волны. Поляризацию единицы объёма среды, содержащей N осцилляторов, можно представить в виде Р = 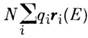. Движение осциллятора в поле световой волны описывается нелинейным ур-нием

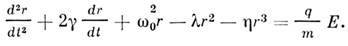
Если решение этого ур-ния ищут в виде ряда по степеням Е, то поляризация среды тоже записывается в виде ряда, а коэф. этого ряда являются Н. в. Из решения этого ур-ния следует, что гармонич. эл--магн. волна индуцирует поляризацию в системе ангармонич.

осцилляторов на частотах w, 2w, 3w и т. д. Оптич. ре-зонансы возникают не только при приближении частот действующих полей к собств. частоте осциллятора w₀, но и при совпадении с ней тех или иных комбинац. частот, поэтому частотная дисперсия Н. в. имеет сложный вид. Напр., кубич. Н. в. даётся выражением

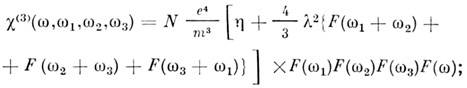
где

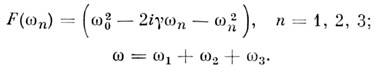
В поле монохроматич. излучения Н. в. c⁽³⁾(3w,w), ответственная за генерацию 3-й гармоники, испытывает резонанс при w = w₀, 2w = w₀ и при 3w = w₀.

Расчёт Н. в. производится также методами квантовой механики. Поляризация P(r,t)связана с электрич. полем, действующим на систему, квантовомеханич. ур-ниями

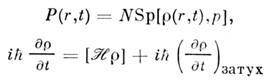
(r - оператор матрицы плотности, р - оператор электрич. дипольного момента, - полный гамильтониан системы), причём восприимчивости n-го порядка можно рассчитывать, решая указанные ур-ния методом возмущений, т. е. представив r(r,t) в виде ряда по возрастающим степеням Е. Т. о. удаётся получить Н. в. любого порядка для системы, состоящей из атомов. Однако детальное описание сложных молекулярных систем в большинстве случаев затруднительно. Ещё труднее рассчитывать Н. в. вблизи электронных переходов в сложных молекулах и конденсиров. средах. Напр., квантовомеханич. описание нелинейных оптич. свойств кристаллов требует детального знания зонной структуры: эфф. масс носителей тока, симметрии зон, правил отбора, дисперсионных соотношений и т. д. Однако в большинстве практич. случаев частоты переходов и волновые функции недостаточно хорошо известны, поэтому для расчёта Н. в. используют разл. приближённые модели [5]. Напр., достаточную точность для расчёта Н. в. даёт модель связей, предполагающая, что индуцированная в кристалле поляризация есть векторная сумма поляризаций, наведённых на всех связях между атомами в единичном объёме, и что идентичные связи в разл. твёрдых телах имеют одинаковые свойства. Взаимодействие между связями не учитывается.

При расчёте Н. в. жидкостей и твёрдых тел необходимо также принимать во внимание фактор локального поля, учитывающий отличие приложенного к среде поля от поля, действующего на отд. молекулу.

Нелинейный отклик отд. атома или молекулы на электрич. поле световой волны - не единств. причина нелинейных оптич. эффектов. Н. в. могут иметь, напр., тепловую природу, когда поглощение света вызывает нагрев, а следовательно, изменение коэф. преломления вещества. К нелинейному изменению коэф. преломления может привести изменение плотности вещества из-за расширения, связанного с квадратичной электро-стрикцией в поле световой волны. В жидкостях и жидких кристаллах существенны нелинейности, обусловленные оптич. ориентацией анизотропных молекул в поле поляризов. лазерной волны. Электронные механизмы нелинейности удаётся отличить от тепловых, стрикционных, ориентационных по временам установления нелинейного отклика и его релаксации, к-рые для электронных процессов, как правило, меньше.

В ряде случаев, как и в линейной оптике, необходимо учитывать влияние на нелинейную поляризацию в выбранной точке среды полей в разл. других точках (нелокальные нелинейнооптич. явления). Относит. вклад нелокальных нелинейных процессов в поляризацию Р среды определяется т. н. параметром пространственной дисперсии d/l(l - длина волны излучения, d - характерный размер в среде: диаметр молекулы, параметр кристаллич. решётки и т. п.). В оптич. диапазоне частот параметр дисперссии пространственной мал: d/K 10^-4-10^-3, и, как правило, вклад эффектов, связанных с не локальностью нелинейного отклика, несуществен. Но в отд. случаях, напр. при исследовании нелинейного изменения поляризац. характеристик света, генерации чётных оптич. гармоник в изотропных веществах, учёт эффектов пространственной дисперсии обязателен. Велика роль пространственной дисперсии в рентг. диапазоне и для объектов с сильной нелокальностью нелинейного отклика, таких как жидкие кристаллы, экситоны в полупроводниках, биол. макромолекулы.

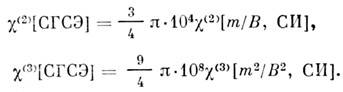
Восприимчивости измеряют, связывая эффективность нелинейного процесса с интенсивностью взаимодействующих в нелинейном процессе волн (напр., в случае генерации 2-й гармоники Н. в. 2-го порядка связывают с интенсивностью накачки) [6,7]. При этом используется информация о пространственно-временном профиле взаимодействующих пучков, их спектральном составе, длине исследуемого образца, его ориентации, поляризации излучения и выполнении условий фазового синхронизма. Абс. измерения оптич. нелинейно-стей - сложная задача, поэтому часто используют относит. измерения. Эталонным кристаллом для относит. измерений 2-й гармоники является кристалл KDP (КН₂РO₄), у к-рого c⁽²⁾ = 1,1^.10^-9 СГСЭ (длина волны накачки l = 1,06 мкм), в ИК-области - кристалл арсенида галлия с c⁽²⁾ = 3,2^.10^-7 СГСЭ (l = = 10,6 мкм). Для поиска новых нелинейных материалов широко применяется методика измерения относит. Н. в. в порошках, позволяющая оценить оптич. нелинейность кристаллов и установить возможность синхронных нелинейных взаимодействий, не располагая большими монокристаллич. образцами. Коэф. преломления подавляющего большинства оптич. материалов отличаются не более чем на порядок, а различие ку-бич. Н. в. составляет более десяти порядков величины.

Нерезонансное значение 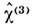для оптич. стёкол и щё-лочно-галоидных кристаллов изменяется в диапазоне (10^-15-10^-13) СГСЭ, напр. для LiF c⁽³⁾ = 4^.10^-15 СГСЭ, для прозрачных жидкостей - в диапазоне (10^-13- 10^-14) СГСЭ, напр. CS₂ имеет c⁽³⁾ = 9^.10¹⁴ СГСЭ. Полупроводниковые кристаллы имеют, как правило, большую нелинейность: для GaAs c⁽³⁾ = 1,5^.10^-10 СГСЭ, для Si c⁽³⁾ = 2^.10^-10 СГСЭ. Удельные (на одну частицу) нерезонансные значения кубич. Н. в. для газов лежат в диапазоне (10^-39-10^-33) СГСЭ, напр. для Аr c⁽³⁾ = 3.10^-38 СГСЭ, для атм. воздуха c⁽³⁾ = = 10^-38 СГСЭ. Резонансные Н. в. для газов могут быть на пять-шесть порядков больше. "Гигантские" Н. в. обнаружены в условиях однофотонного резонанса поглощения в узкозонных полупроводниках [для InSb, HgCdTe c⁽³⁾ = (10^-1-10^-4) СГСЭ]. Исключительно большая нелинейность c⁽³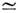⁾ (10^-2 - 10^-8) СГСЭ связана с резонансными процессами поглощения с участием экситонов и биэкситонов в полупроводниках [8]. Коллективные ориентац. нелинейности в жидких кристаллах достигают величины c⁽³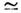⁾(10^-1-10^-2) СГСЭ. При этом время установления нелинейного отклика ~ 1 с.

Нелинейности высших порядков c⁽ⁿ⁾ (п >= 3) существенны для описания таких эффектов, как генерация высших оптич. гармоник в газах и кристаллич. средах, многофотонное поглощение, многофотонная ионизация атомов; ими объясняются ограничение диаметра фокального пятна при самофокусировке света, насыщение эффективности нелинейных процессов при высоких уровнях оптич. возбуждения. При расчёте и измерении высших (п >= 3) Н. в. нелинейнооптич. процессы разделяют на "прямые" и "каскадные" [5]. Напр., 3-я оптич. гармоника в нелинейной среде без центра инверсии может возникнуть как в результате процесса нелинейного смешения трёх волн накачки одинаковой частоты на Н. в. c⁽³⁾, так и каскадно (ступенчато) при генерации 2-й оптич. гармоники и сложении двух волн с частотами 2w и w. Такой комбиниров. процесс может быть описан в терминах эфф. кубич. нелинейностей, причём

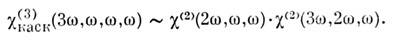
В более общем случае

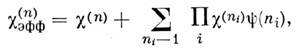
причём функции y(n_i) определяются линейными дисперсионными свойствами среды. Свойства симметрии тензоров c_каск⁽ⁿ⁾ и c⁽ⁿ⁾, как правило, идентичны.

Нерезонансные значения величин Н. в. высоких порядков невелики, напр. Н. в. кристалла формиата лития для генерации 4-й гармоники c⁽⁴⁾ ~ 1^.10^-21 СГСЭ, значение восприимчивости 5-го порядка для кристалла кальцита c⁽⁵⁾ ~ 1^.10^-27 СГСЭ. Удельные (на один атом) нерезонансные Н. в. паров Na, К, Rb, Li измерены вплоть до c⁽⁹⁾; напр., для натрия в единицах СГСЭ: c⁽³⁾ = 8,1^.10^-34, c⁽⁵⁾ = 1,7^.10^-43, c⁽⁷⁾ = 7,0^.10^-69, c⁽⁹⁾ = -4,3^.10^-59.

Сильный нелинейный отклик. Концепция Н. в. успешно используется для описания большинства задач нелинейной оптики, однако она имеет ограниченную область применения. В мощных световых полях или в сильнонелинейных средах высшие члены разложения поляризации перестают быть малыми: 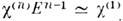, тогда разложение (1) теряет смысл, а соответствующий ряд (2) перестаёт сходиться. Такие проблемы возникают, в частности, при исследовании насыщения перехода в системе двухуровневых атомов в поле эл--магн. волны или при описании сильно возбуждённых полупроводниковых кристаллов, когда их отклик на внеш. световое воздействие перестаёт быть однозначной функцией интенсивности света, т. е. наблюдаются оптич. гистерезисные явления (напр., гистерезис преломления или поглощения нелинейной средой, оптическая бистабильность и неустойчивость). В этом случае материальные ур-ния могут быть записаны только в неявном виде f(Е, Р) = 0. Напр., для сильнонелинейной изотропной гиротропной среды с учётом кубич. нелинейности ангармонич. осцилляторов, составляющих молекулы, можно записать [9]:

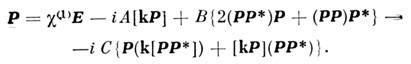
Здесь А, В, С - частотно-зависимые кооф., k - волновой вектор. Это ур-ние имеет более широкую, чем (3), область применимости и допускает гистерезисные решения для поляризации Р.

Литература по нелинейным восприимчивостям

1. Ахманов С. А., Хохлов Р. В., Проблемы нелинейной оптики, М., 1964;
2. Бломберген Н., Нелинейная оптика, пер. с англ., М., 1966;
3. Шен И. Р., Принципы нелинейной оптики, пер. с англ., М., 1989;
4. Сиротин Ю. И., Шаскольская М. П., Основы кристаллофизики, 2 изд., М., 1979;
5. Нелинейная спектроскопия, под ред. Н. Бломбер-гена, пер. с англ., М., 1979;
6. Справочник по лазерам, пер. с англ., под ред. А. М. Прохорова, т. 2, М., 1978;
7. Церни-ке Ф., Мидвинтер Д ж., Прикладная нелинейная оптика, пер. с англ., М., 1976;
8. "Journal of the Optical Society of America", 2B, Special issue, Excitonic Optical Nonlir.earities, 1985;
9. Ахманов С. А., ЖелудевН. И., Свирко Ю. П., Неустойчивость поляризации световой волны в сильнонелинейной среде, "Изв. АН СССР, Сер. физ.", 1982, т. 46, с. 1070.

Н. И. Жёлудев

к библиотеке   к оглавлению   FAQ по эфирной физике   ТОЭЭ   ТЭЦ   ТПОИ   ТИ  

Знаете ли Вы, что, как и всякая идолопоклонническая религия, релятивизм ложен в своей основе. Он противоречит фактам. Среди них такие:

1. Электромагнитная волна (в религиозной терминологии релятивизма - "свет") имеет строго постоянную скорость 300 тыс.км/с, абсурдно не отсчитываемую ни от чего. Реально ЭМ-волны имеют разную скорость в веществе (например, ~200 тыс км/с в стекле и ~3 млн. км/с в поверхностных слоях металлов, разную скорость в эфире (см. статью "Температура эфира и красные смещения"), разную скорость для разных частот (см. статью "О скорости ЭМ-волн")

2. В релятивизме "свет" есть мифическое явление само по себе, а не физическая волна, являющаяся волнением определенной физической среды. Релятивистский "свет" - это волнение ничего в ничем. У него нет среды-носителя колебаний.

3. В релятивизме возможны манипуляции со временем (замедление), поэтому там нарушаются основополагающие для любой науки принцип причинности и принцип строгой логичности. В релятивизме при скорости света время останавливается (поэтому в нем абсурдно говорить о частоте фотона). В релятивизме возможны такие насилия над разумом, как утверждение о взаимном превышении возраста близнецов, движущихся с субсветовой скоростью, и прочие издевательства над логикой, присущие любой религии.

4. В гравитационном релятивизме (ОТО) вопреки наблюдаемым фактам утверждается об угловом отклонении ЭМ-волн в пустом пространстве под действием гравитации. Однако астрономам известно, что свет от затменных двойных звезд не подвержен такому отклонению, а те "подтверждающие теорию Эйнштейна факты", которые якобы наблюдались А. Эддингтоном в 1919 году в отношении Солнца, являются фальсификацией. Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМА Рыцари теории эфира

10.11.2021 - 12:37: ПЕРСОНАЛИИ - Personalias -> WHO IS WHO - КТО ЕСТЬ КТО - Карим_Хайдаров. 10.11.2021 - 12:36: СОВЕСТЬ - Conscience -> РАСЧЕЛОВЕЧИВАНИЕ ЧЕЛОВЕКА. КОМУ ЭТО НАДО? - Карим_Хайдаров. 10.11.2021 - 12:36: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от д.м.н. Александра Алексеевича Редько - Карим_Хайдаров. 10.11.2021 - 12:35: ЭКОЛОГИЯ - Ecology -> Биологическая безопасность населения - Карим_Хайдаров. 10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> Проблема государственного терроризма - Карим_Хайдаров. 10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> ПРАВОСУДИЯ.НЕТ - Карим_Хайдаров. 10.11.2021 - 12:34: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вадима Глогера, США - Карим_Хайдаров. 10.11.2021 - 09:18: НОВЫЕ ТЕХНОЛОГИИ - New Technologies -> Волновая генетика Петра Гаряева, 5G-контроль и управление - Карим_Хайдаров. 10.11.2021 - 09:18: ЭКОЛОГИЯ - Ecology -> ЭКОЛОГИЯ ДЛЯ ВСЕХ - Карим_Хайдаров. 10.11.2021 - 09:16: ЭКОЛОГИЯ - Ecology -> ПРОБЛЕМЫ МЕДИЦИНЫ - Карим_Хайдаров. 10.11.2021 - 09:15: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Екатерины Коваленко - Карим_Хайдаров. 10.11.2021 - 09:13: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вильгельма Варкентина - Карим_Хайдаров.