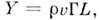 где
где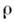 - плотность среды.
- плотность среды.
Подъемная сила - сила, перпендикулярная
вектору скорости движения центра тяжести тела, возникающая вследствие несимметрии
обтекания тела потоком жидкости (газа). В двумерной модели движения крыла
в идеальной и несжимаемой жидкости (рис. 1) несимметричное движение жидкости
у границ крыла можно представить как сумму поступат. движения со скоростью
v и
циркуляц. движения интенсивностью Г. В суммарном течении при выбранном
направлении циркуляции скорость у ниж. границы профиля будет меньше, а
давление больше, чем у верхней (см. Бернулли уравнение ).Интеграл
от давления по контуру профиля крыла даст П. с. Y, перпендикулярную
скорости набегающего потока v. П. с. Y будет зависеть от
величины циркуляции скорости Г и, согласно Жуковского теореме, для
участка крыла длиной L (вдоль размаха)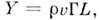 где
где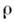 - плотность среды.
- плотность среды.

Рис. 1. Схема обтекания профиля крыла самолёта. Скорость vн < vв, давление pн> рв.
Поскольку Г имеет размерность [vl]
([l] - размерность длины), то П. с. можно выразить равенством где S - величина характерной для тела площади (напр., площадь крыла
в плане, равная Lb, если b - длина хорды профиля крыла),
Су - безразмерный коэф. П. с., зависящий в общем случае от формы тела,
его ориентации в среде и чисел Рейнольдса Re и Маха
М. Значение
Суопределяют
теоретич. расчётом или экспериментально. Так, согласно теории Жуковского,
для крыла бесконечного размаха в плоскопараллельном потоке при небольших
углах атаки
где S - величина характерной для тела площади (напр., площадь крыла
в плане, равная Lb, если b - длина хорды профиля крыла),
Су - безразмерный коэф. П. с., зависящий в общем случае от формы тела,
его ориентации в среде и чисел Рейнольдса Re и Маха
М. Значение
Суопределяют
теоретич. расчётом или экспериментально. Так, согласно теории Жуковского,
для крыла бесконечного размаха в плоскопараллельном потоке при небольших
углах атаки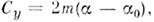 где
где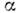 - угол атаки (угол между направлением скорости набегающего потока и хордой
крыла),
- угол атаки (угол между направлением скорости набегающего потока и хордой
крыла),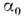 -
угол атаки при нулевой П. с., m - коэф., зависящий только от формы
профиля крыла, напр. для тонкой слабоизогнутой пластины т =
-
угол атаки при нулевой П. с., m - коэф., зависящий только от формы
профиля крыла, напр. для тонкой слабоизогнутой пластины т =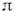 .
В случае крыла конечного размаха L коэф. т =
.
В случае крыла конечного размаха L коэф. т =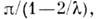 где
где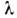 =
L/b - удлинение крыла. Методы вычисления П. с. обобщены на случай обтекания
решётки профилей и используются при расчёте лопаточных машин (насосов,
компрессоров и турбин).
=
L/b - удлинение крыла. Методы вычисления П. с. обобщены на случай обтекания
решётки профилей и используются при расчёте лопаточных машин (насосов,
компрессоров и турбин).
В реальной жидкости в результате влияния
вязкости величина т меньше теоретической, причём эта разница возрастает
по мере увеличения относит. толщины профиля; значение угла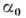 также
меньше теоретического. Кроме того, с увеличением угла
также
меньше теоретического. Кроме того, с увеличением угла зависимость Су от
зависимость Су от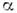 (рис. 2) перестаёт быть линейной и величина dCy/
(рис. 2) перестаёт быть линейной и величина dCy/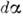 монотонно убывает, становясь равной нулю при угле атаки
монотонно убывает, становясь равной нулю при угле атаки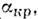 к-рому соответствует макс. величина коэф. П. с. Сумакс.
Дальнейшее увеличение
к-рому соответствует макс. величина коэф. П. с. Сумакс.
Дальнейшее увеличение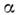 ведёт к падению Су вследствие отрыва пограничного слоя от верх.
поверхности крыла и возрастания давления на ней. Величина Сумакс
имеет существ. значение, т. к. чем она больше, тем меньше скорость взлёта
и посадки самолёта.
ведёт к падению Су вследствие отрыва пограничного слоя от верх.
поверхности крыла и возрастания давления на ней. Величина Сумакс
имеет существ. значение, т. к. чем она больше, тем меньше скорость взлёта
и посадки самолёта.
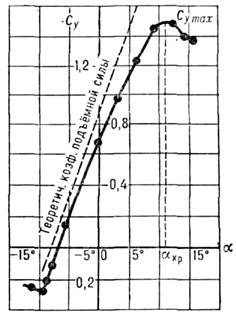
Рис. 2. Зависимость Суот a.
При больших, но докритич. скоростях, т.
е. таких, для к-рых М < Мкр (Мкр
- значение числа М набегающего потока, при к-ром вблизи поверхности
профиля местные значения числа М = 1), становится существенной сжимаемость
газа. Для слабопзогнутых и тонких профилей при малых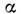 сжимаемость можно приближённо учесть, положив
сжимаемость можно приближённо учесть, положив
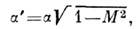
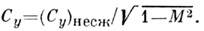
При сверхзвуковых скоростях характер обтекания
существенно меняется. Так, при обтекании плоской пластины идеальным сжимаемым
газом у её передней кромки на верх. поверхности образуются волны разрежения,
а на нижней - ударная волна (рис. 3). В результате давление рнна
ниж. поверхности пластины становится больше, чем на верхней (рв);
возникает суммарная сила, нормальная к поверхности пластины, составляющая
к-рой, перпендикулярная к скорости набегающего потока, и есть П. с. Для
малых М > 1 и малых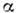 П. с. пластины может быть вычислена по ф-ле Су =
П. с. пластины может быть вычислена по ф-ле Су =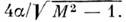 Эта
ф-ла справедлива и для тонких профилей произвольной формы с острой передней
кромкой.
Эта
ф-ла справедлива и для тонких профилей произвольной формы с острой передней
кромкой.
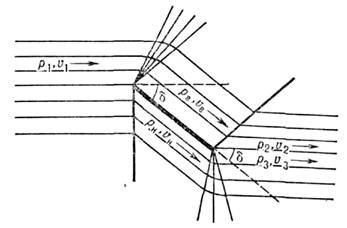
Рис. 3. Схема сверхзвукового обтекания пластинки: vв > vн, рв < рн; v2 < vв, р2 > рв; vн< v1, рн> р1, v3 > vн, р3< рн.
При обтекании тел сложной формы, напр. спускаемых в атмосфере Земли и планет космич. летат. аппаратов, П. с. определяют эксперим. путём на основании испытаний геометрически подобных моделей в аэродинамич. трубах и газодинамич. стендах.

М. Я. Юделович
|
|