к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

РЕАЛЬНАЯ ФИЗИКА

Глоссарий по физике

А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

Циркуляция скорости

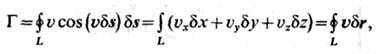
Циркуляция скорости - кинематич. характеристика течения жидкости или газа, служащая мерой завихренности течения. Циркуляция скорости представляется криволинейным интегралом по замкнутой кривой L от произведения проекции скорости u на касательную к кривой на элемент длины этой кривой ds:

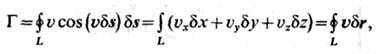
где u-модуль скорости, u_x, u_y и u_z- проекции скорости на оси координат, d_х, d_y и d_z - проекции направленного элемента dr дуги L на те же оси. По Стокса формуле циркуляция скорости связана с потоком вихря w = rot u через произвольную поверхность S, опирающуюся на кривую L, равенством

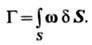
Согласно кинематич. теореме Томсона (Кельвина), индивидуальная, или субстанциональная, производная по времени от циркуляции скорости по жидкому (состоящему всё время из одних и тех же частиц) замкнутому контуру равна циркуляции ускорения по тому же контуру (точка над буквой - символ индивидуальной производной по времени):

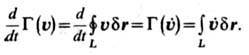
Если циркуляция скорости равна нулю по любому контуру, проведённому внутри жидкости, то течение жидкости - безвихревое, или потенциальное, и потенциал скоростей - однозначная функция координат. Если же циркуляция скорости по некоторым контурам отлична от нуля, то течение жидкости либо вихревое в соответственных областях, либо безвихревое, но с неоднозначным потенциалом скоростей (область течения многосвязная). В случае потенциального течения в многосвязной области циркуляция скорости по всем контурам, охватывающим одни и те же твёрдые границы, имеет одно и то же значение. Циркуляция скорости широко используется как характеристика течений идеальной (без учёта вязкости) жидкости. По динамич. теореме Томсона (Кельвина) циркуляция скорости по замкнутому жидкому контуру остаётся постоянной во время движения, если, во-первых, жидкость является идеальной, во-вторых, давление (газа) жидкости зависит только от плотности, в-третьих, массовые силы потенциальны, а потенциал однозначен. Для вязкой жидкости циркуляция скорости со временем изменяется вследствие диффузии вихрей. При плоском циркуляционном обтекании контура идеальной несжимаемой жидкостью, при котором скорость на бесконечности отлична от нуля, воздействие жидкости на контур определяется по Жуковского теореме и прямо пропорционально значению циркуляции скорости, плотности жидкости и значению скорости потока на бесконечности. При плоском обтекании идеальной жидкостью крыла с острой задней кромкой величина циркуляции скорости определяется Чаплыгина - Жуковского постулатом. При обтекании крыла конечной размаха, хорда к-рого в плане меняется, циркуляция скорости вдоль размаха крыла также меняется.

Лит. см. при ст. Механика. Л. Г. Лойцянский.

к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

Знаете ли Вы, что низкочастотные электромагнитные волны частотой менее 100 КГц коренным образом отличаются от более высоких частот падением скорости электромагнитных волн пропорционально корню квадратному их частоты от 300 тысяч кмилометров в секунду при 100 кГц до примерно 7 тыс км/с при 50 Гц.

НОВОСТИ ФОРУМА

Рыцари теории эфира