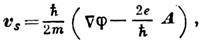
Согласно теории сверхпроводимости, сверхпроводящие (спаренные) электроны, создающие ток (см. Купера эффект), обладают единой волновой функцией, характеризующейся нек-рой фазой j (фазовая когерентность сверхпроводящих электронов). Наличие фазовой когерентности и обусловливает квантование магнитного потока. В замкнутом сверхпроводящем кольце (рис.) разность фаз волновой функции между точками А и В, jAB = jA-jB, удовлетворяет соотношению Джозефсона:
h(дjАB/дt) = 2eV, (1)
где V - разность потенциалов между точками А и В контура l (контур изображён штриховой линией). С др. стороны, согласно закону электромагнитной индукции, напряжение между точками А и В
V = -дФ/дt, (2)
где Ф - магн. поток, заключённый внутри контура l. Из ур-ний (1) и (2) следует, что
jAB - 2p(Ф/Ф0) = const.
Постоянная интегрирования в этом выражении связана со скоростью сверхпроводящих электронов, что следует из квантовомеханич. выражения для скорости куперовских пар:
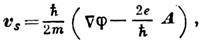
где т - масса электрона, А - вектор-потенциал эл--магн. поля. Интегрирование vs по контуру l между точками А и В даёт след. выражение:
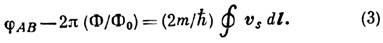
Если сверхпроводящее кольцо выполнено из массивного сверхпроводника толщиной больше глубины проникновения магн. поля, то, в силу Мейснера эффекта ,в глубине сверхпроводника ток отсутствует и vs=0. Следовательно, в массивном сверхпроводнике
ФAB = 2pФ/Ф0.
В силу однозначности волновой функции разность фаз при совмещении точек А и В должна быть кратной 2p, т. е. jAB=2pn, где п - целое число. Т. о., магн. поток, проходящий через контур l (кольцо), оказывается квантованным: Ф=Ф0п. При этом мейснеровские токи, экранирующие магн. поле внутри сверхпроводника, распределяется так, что не пускают "лишние" магн. силовые линии внутрь кольца. Фундаментальность явления квантования магнитного потока сказывается, напр., в существовании квантованных вихрей в сверхпроводниках второго рода, определяющих эл--магн. свойства большого класса сверхпроводников. Квантование магнитного потока наряду с эффектом Джозефсона составляет основу работы сверхпроводящих квантовых интерферометров (сквидов)и др. сверхпроводящих криогенных приборов [4, 5]. Родственным эффекту квантованию магнитного потока является неполное квантование магнитного потока в тонком сверхпроводящем кольце. Если кольцо выполнено из сверхпроводника толщиной меньше глубины проникновения магнитного поля, то скорость сверхпроводящих электронов в нём всюду отлична от нуля. Из выражения (3) следует, что
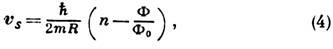
где R - радиус кольца. Целое число п принимает такие значения, при к-рых скорость имеет по возможности наименьшую величину. Т. о., выражение (4) определяет осцилляционную зависимость vs от магн. потока с периодом Ф0. Наличие внутреннего движения сверхпроводящих электронов сказывается на температуре Тс перехода в сверхпроводящее состояние, что приводит к осцилляционной зависимости Тс и связанных с ней характеристик (напр., сопротивления) от магнитного поля.
Н. Б. Копнин
1. Электромагнитная волна (в религиозной терминологии релятивизма - "свет") имеет строго постоянную скорость 300 тыс.км/с, абсурдно не отсчитываемую ни от чего. Реально ЭМ-волны имеют разную скорость в веществе (например, ~200 тыс км/с в стекле и ~3 млн. км/с в поверхностных слоях металлов, разную скорость в эфире (см. статью "Температура эфира и красные смещения"), разную скорость для разных частот (см. статью "О скорости ЭМ-волн")
2. В релятивизме "свет" есть мифическое явление само по себе, а не физическая волна, являющаяся волнением определенной физической среды. Релятивистский "свет" - это волнение ничего в ничем. У него нет среды-носителя колебаний.
3. В релятивизме возможны манипуляции со временем (замедление), поэтому там нарушаются основополагающие для любой науки принцип причинности и принцип строгой логичности. В релятивизме при скорости света время останавливается (поэтому в нем абсурдно говорить о частоте фотона). В релятивизме возможны такие насилия над разумом, как утверждение о взаимном превышении возраста близнецов, движущихся с субсветовой скоростью, и прочие издевательства над логикой, присущие любой религии.
4. В гравитационном релятивизме (ОТО) вопреки наблюдаемым фактам утверждается об угловом отклонении ЭМ-волн в пустом пространстве под действием гравитации. Однако астрономам известно, что свет от затменных двойных звезд не подвержен такому отклонению, а те "подтверждающие теорию Эйнштейна факты", которые якобы наблюдались А. Эддингтоном в 1919 году в отношении Солнца, являются фальсификацией. Подробнее читайте в FAQ по эфирной физике.
|
|
 |
