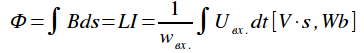
L - индуктивность катушки;
I - электрический ток, протекающий по катушке;
Обратный этому процессу процесс:
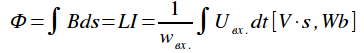
Различают два типа магнитоэлектрической индукции. Один из них - Фарадеев, - состоит в наведении вихревого электрического поля Е(r, t) переменным магнитным полем В(r, t):
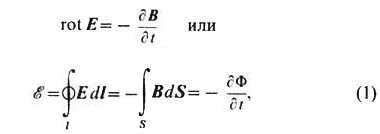
где S - поверхность, ограниченная фиксированным контуром l, Ф - магнитный поток через S (направления нормали к S и обхода по контуру l связаны правилом правого винта). Соотношения (1) являются строгими уравнениями классической электродинамики (см. Максвелла уравнения) и универсально применимы как к свободному пространству (эфиру, вакууму), так и к произвольным средам и системам (неподвижным и движущимся).
В простейших случаях замкнутых неподвижных квазистационарных электрических
цепей, выполненных из достаточно тонких проводов, циркуляция электрического
поля 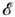 в (1) может приближённо
трактоваться как электродвижущая сила
(э.д.с.) магнитоэлектрической индукции в "проводящем контуре"
в (1) может приближённо
трактоваться как электродвижущая сила
(э.д.с.) магнитоэлектрической индукции в "проводящем контуре"
![]() ,
если контурный интеграл в (1) слабо зависит от выбора пути интегрирования внутри проводника. Э.д.с. магнитоэлектрической индукции определяется через работу электрического поля над током в единицу времени (Р):
,
если контурный интеграл в (1) слабо зависит от выбора пути интегрирования внутри проводника. Э.д.с. магнитоэлектрической индукции определяется через работу электрического поля над током в единицу времени (Р):
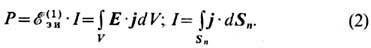
Здесь j(r, t) -
плотность тока в проводнике,
I - электрический ток, который в квазистационарном приближении
считается одинаковым для всех нормальных сечений Sn
проводящего контура. В тех случаях, когда зависимостью Е
и j от координат поперечного сечения проводника
можно пренебречь, выражение (2) преобразуется к виду (1) подстановкой:
j=lI/Sn;
dV=Sndl; dl=ldl. Такая ситуация обычно имеет место при внешней магнитоэлектрической индукции, когда поток Ф можно считать сторонним, независимым от наводимых в контуре токов j, создаваемым, например, достаточно удалёнными источниками. Напротив, при самоиндукции, когда э.д.с. в цепи наводится магнитным полем, создаваемым переменным током в той же цепи, магнитное поле всегда существенно изменяется от точки к точке нормального сечения провода. В этом случае, а также для более точных расчётов э.д.с. внешней магнитоэлектрической индукции производят усреднение в (2) по линиям
тока в проводе: 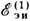 = -д<Фi>/дt, где Фi
- магнитный поток через поверхность Si, ограниченную линией тока
li, <...> - знак усреднения. Поток
= -д<Фi>/дt, где Фi
- магнитный поток через поверхность Si, ограниченную линией тока
li, <...> - знак усреднения. Поток 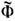 = <Фi> называется сцепленным с контуром магнитным потоком.
= <Фi> называется сцепленным с контуром магнитным потоком.
Другой тип эффектов магнитоэлектрической индукции - Лоренцев, связан с движением материальных сред (проводников, изоляторов, твердых тел, жидкостей, газов, плазмы) в стационарном магнитном поле В (r). На заряженные частицы в движущихся телах действует магнитная Лоренца сила Fm = e[uB](u - скорость носителей заряда), приводящая к разделению зарядов противоположных знаков, к генерации электрических токов в проводниках, к поляризации диэлектриков. Индуцируемые электрические поля при этом потенциальны (rot E = - (дB/дt = 0). Усреднённые по физически малому объёму силы Fm имеют плотность fm = [jВ] и совершают механическую работу с мощностью
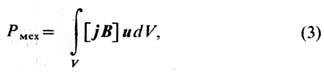
где u = <u> - средняя
скорость носителей заряда. Э.д.с. магнитоэлектрической индукции
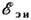 определяется из соотношения
определяется из соотношения

которое следует из равенства нулю суммарной работы сил Лоренца (Fm | u).
Как видно из (4), при магнитоэлектрической индукции Лоренцевам типа происходит преобразование механической энергии в электромагнитную, если 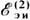 .I >
0 (как это имеет место в динамо-машинах) или, наоборот, электромагнитной - в
механическую, если
.I >
0 (как это имеет место в динамо-машинах) или, наоборот, электромагнитной - в
механическую, если 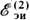 .I<0 (в электродвигателях).
.I<0 (в электродвигателях).
Для электрических цепей, состоящих из тонких проводников, можно (так же, как это делалось выше) перейти от интегрирования по объёму в (3) к интегрированию вдоль некоторого контура внутри провода:
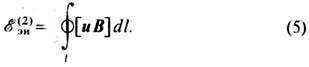
В твердых телах с электронной или дырочной проводимостью поперечная
(к dl и В)
составляющая скорости и определяется локальным значением скорости контура
uk(r, t)
(и|=uk |), что позволяет объединить э.д.с. 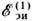 и
и 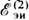 :
:
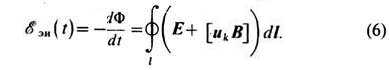
Это соотношение носит название закона Фарадея. В отличие от (1) выражение (6) справедливо только в квазистационарном приближении. Полная производная по времени от магнитного потока Ф учитывает его изменения, связанные как с изменением поля во времени, так и с движением (деформацией) проводящего контура.
Для проводников с произвольным механизмом проводимости (электролитов,
плазмы, твердых тел со смешанной электронно-дырочной проводимостью) закон
Фарадея в общем случае неприменим, т. к. движение проводника не определяет
однозначно поперечную скорость носителей заряда u.
В таких средах противоположные заряды могут рождаться парами (ионизация,
диссоциация, квантовые переходы из заполненной зоны в свободную) и
аннигилировать (рекомбинация, обратные квантовые переходы). Могут возникать
также вихревые конвективные движения пар заряженных частиц. Всё это может
приводить к относительному поперечному движению зарядов в проводнике.
Так, напр., на рис. 1 проводящая перемычка А движется со скоростью
UА вдоль проводов, помещённых в однородное постоянное
магнитное поле В0. Если перемычкой является
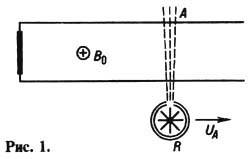
металлическая шина, то в цепи наводится 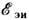 в соответствии с (6). Если же цепь замыкается волной ионизации воздуха, создаваемой,
напр., движущимся источником g-излучения (R)или дуговым разрядом,
то
в соответствии с (6). Если же цепь замыкается волной ионизации воздуха, создаваемой,
напр., движущимся источником g-излучения (R)или дуговым разрядом,
то 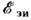 в цепи
не возникает, так как проводимость плазменного столба обеспечивают электрон-ионные
пары, рождающиеся в среднем с нулевой начальной скоростью и через некоторое время рекомбинирующие. Наоборот, если неподвижный разряд продувать струёй воздуха перпендикулярно магнитному полю, э.д.с. магнитоэлектрической индукции будет наводиться [в соответствии с (5), хотя dФ/dt
= 0]. Э.д.с. магнитоэлектрической индукции будет возникать и в том случае, если разряд неподвижен
и нет стороннего продува, но в цепь включена дополнительная э.д.с., создающая сторонний
ток. Такой разряд будет всасывать со всех сторон окружающий воздух и выбрасывать
его в виде струи в сторону действия силы Ампера.
в цепи
не возникает, так как проводимость плазменного столба обеспечивают электрон-ионные
пары, рождающиеся в среднем с нулевой начальной скоростью и через некоторое время рекомбинирующие. Наоборот, если неподвижный разряд продувать струёй воздуха перпендикулярно магнитному полю, э.д.с. магнитоэлектрической индукции будет наводиться [в соответствии с (5), хотя dФ/dt
= 0]. Э.д.с. магнитоэлектрической индукции будет возникать и в том случае, если разряд неподвижен
и нет стороннего продува, но в цепь включена дополнительная э.д.с., создающая сторонний
ток. Такой разряд будет всасывать со всех сторон окружающий воздух и выбрасывать
его в виде струи в сторону действия силы Ампера.
Другие ограничения применимости закона Фарадея (6) возникают в распределённых
проводящих средах и коммутирующих устройствах со скользящими контактами,
переключателями, коллекторами и т. п., т. е. в системах, геометрия которых не
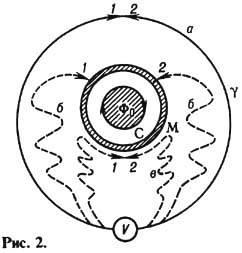
определяет однозначно структуру индукционных токов. Рис. 2 иллюстрирует т.н.
парадокс Геринга. Постоянный магнитный поток Ф0, сосредоточенный внутри соленоида С, пронизывает проводящий контур γ в его начальном положении а. Контур с помощью скользящих
контактов 1, 2 и проводящего кольца М переводится
в положение б, в к-ром поток через контур Фγ = 0. Магнитный поток через γ меняется за конечное время, контур
всё время остаётся замкнутым, однако э.д.с. не возникает, стрелка вольтметра
(V)не отклоняется 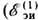 =0, т.к. dB/dt = 0;
=0, т.к. dB/dt = 0; 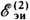 = 0, т.к. В = 0 в областях, где и
= 0, т.к. В = 0 в областях, где и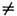 0).
0).
Магнитоэлектрическая индукция приводит к поляризации движущихся в магнитном поле диэлектриков. Вектор поляризации
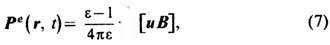
где ε - диэлектрическая проницаемость,
и ( r, t)-локальная скорость среды. Неоднородность и( r),
В(r)или e(r)приводит к появлению объёмного индуцированного заряда с плотностью rе= - divPe; на границе диэлектрика с вакуумом наводится
поверхностный заряд 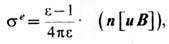 где n
- внешняя единичная нормаль к поверхности.
где n
- внешняя единичная нормаль к поверхности.
Явление магнитоэлектрической индукции открыто М. Фарадеем (М. Faraday) в 1831 и независимо Дж. Генри (J. Henry) в 1832. Э. X. Ленц в 1833 установил универсальное правило для определения знака э.д.с. магнитоэлектрической индукции. В 1845 Ф. Нейман (F. Neumann) дал математическую формулировку закона Фарадея (6). Универсальная общность отвлечённого от свойств конкретных материальных сред соотношения (1), которое иногда тоже называется законом Фарадея, была понята Дж. К. Максвеллом в 1864. Им же предсказан дополнительный к магнитоэлектрической индукции эффект - наведение магнитного поля переменным электрическим. Открытие электромагнитной и магнитоэлектрической индукций привело к формированию представления о едином материальном электромагнитном поле (тензорном), компонентами которого являются напряжённости электрического и магнитного полей.
Явление магнитоэлектрической индукции чрезвычайно широко реализуется в природе и применяется в технике. На эффектах магнитоэлектрической индукции базируется устройство электромоторов и генераторов тока разного типа, трансформаторов, измерительных приборов, индукционных нагревателей, ускорителей элементарных частиц, источников плазмы в термоядерных реакторах, электромагных движителей, магнитных подвесок и т. д.
Эффекты магнитоэлектрической индукции в распределённых системах порождают такие явления, как токи Фуко, униполярную индукцию, гидромагнитное динамо, магнитную вязкость, неустойчивость плазменных шнуров. Магнитоэлектрическая индукция лежит в основе механизма распространения электромагнитных волн.

М. А. Миллер, Г. В.
Пермитин.
|
|