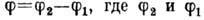Джозефсона эффект. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Джозефсона эффект - протекание сверхпроводящего тока через тонкую изолирующую или несверхпроводящую прослойку между двумя сверхпроводниками (т. н. джозефсоновский контакт). Эффект был теоретически предсказан Б. Джозефсоном (В. Josephson, 1962) [1]. Д. э. обнаруживается при изучении вольт-амперной характеристики (BAX) джозефсоновских контактов (ДК). При пропускании через ДК достаточно слабого тока напряжение на контакте отсутствует, т. е. ток является чисто сверхпроводящим (джозефсоновский ток). Его существование связано с неполным разрушением куперовских пар электронов (см. Купера эффект) при их прохождении через очень тонкую несверхпроводящую прослойку. Такой режим называется стационарным Д. э. (экспериментально обнаружен в 1963 [2]). При увеличении тока через контакт и достижении им нек-рой величины I_C на контакте возникает напряжение. Значение критич. джозеф-соновского тока I_С зависит от свойств контакта, температуры и магн. поля. Ток I_С складывается из тока сверхпроводящих (спаренных) электронов, к-рый теперь становится переменным (его частота зависит от напряжения на контакте), и тока, обусловленного прохождением через прослойку нормальных (несверхпроводящих) электронов. Режим при токе I_С наз. нестационарным Д. э.

Согласно теории сверхпроводимости, сверхпроводящие (спаренные) электроны характеризуются единой волновой функцией, фаза к-рой плавно меняется вдоль сверхпроводника при протекании по нему тока (фазовая когерентность сверхпроводящих электронов). При прохождении сверхпроводящих электронов через несверхпроводящую прослойку фазовая когерентность частично (в меру отношения толщины прослойки к т. н. длине когерентности) разрушается и протекание джозефсоновского тока через прослойку сопровождается скачком фазы волновой функции сверхпроводящих электронов на этой прослойке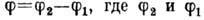

- фазы волновой функции в сверхпроводниках по обe стороны от прослойки. При этом ток через контакт равен

Из ф-лы (1) видно,что джозефсоновский ток не может превышать I_С.

Величина I_С и механизм прохождения электронов через прослойку зависят от типа прослойки. Одним из типичных примеров ДК является туннельный контакт, состоящий из двух одинаковых или разл. сверхпроводников (обычно в виде тонких плёнок), разделённых очень тонким слоем диэлектрика, напр. слоем окисла материала одного из сверхпроводящих электродов. Протекание тока через прослойку в этом случае обусловлено квантовым туннелированием электронов (см. Туннельный эффект) через непроводящий барьер. Для получения измеримого джозефсоновского тока толщина изолирующей прослойки должна быть ок. 10-20 А. На рис. для примера изображена типичная BAX для туннельного контакта из одинаковых сверхпроводников. Стрелками показано направление изменения тока. Если увеличивать ток, то происходит описанный выше переход из стационарного в нестационарный режим Д. э. При уменьшении тока нестационарный Д. э. может сохраниться до значений тока, меньших критического (т. е. туннельный контакт проявляет гистерезис).

Вольт-амперная характеристика (BAX) туннельного контакта Sn- Sn при температуре 1,4 К (прослойка - плёнка оксида олова).

При нестационарном Д. э. разность фаз на контакте зависит от времени:

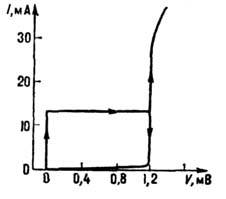
где V - напряжение на контакте, е - заряд электрона. Ур-ние (2) является следствием Шрёдингера уравнения для волновой функции пары сверхпроводящих электронов при наличии постоянной потенц. энергии 2eV и не связано с наличием прослойки, а имеет общий характер. Частота w сверхпроводящего тока через контакт определяется соотношением:

Соотношения (2) и (3) называются соотношениями Джозефсона.

Нестационарный Д. э можно рассматривать также как прохождение сверхпроводящих электронов через прослойку, сопровождающееся изменением их энергии на величину 2eV в расчёте на каждую куперовскую пару. При этом процессе испускаются кванты эл.- магн. излучения с частотой

, связанной с изменением энергии соотношением (3). T. о., при нестационарном Д. э. контакт, находящийся при пост. напряжении, генерирует перем. сверхпроводящий ток. Имеет место и обратный процесс: при облучении джозефсоновского контакта СВЧ-излучением с частотой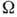

, удовлетворяющей условию

(п - целое число), прохождение сверхпроводящих электронов через контакт происходит с поглощением п фотонов внеш. поля, что приводит к появлению дополнит. тока через контакт, т. е. к возникновению на BAX участков с нулевым дифференциальным сопротивлением. Наблюдение таких участков и явилось первым косвенным обнаружением нестационарного Д. э. в 1963 [3]. Прямое наблюдение генерации СВЧ-излучения джозефсоновским контактом, находящимся под пост. напряжением, было осуществлено в 1965 [4].

Кроме туннельных структур джозефсоновские контакты могут представлять собой т. н. слабосвязанные сверхпроводники, т. е. два сверхпроводника, соединённых узким и коротким сверхпроводящим или нормальным "мостиком", тонкой прослойкой нормального металла либо с помощью точечного контакта. Аналог нестационарного Д. э. наблюдается также в очень узких однородных сверхпроводящих проволочках, где джозефсоновская генерация возникает при пропускании достаточно большого тока. Совокупность явлений, связанных с Д. э. в разл. системах, носит назв. слабой сверхпроводимости [5,6,7].

Д. э. подтверждает осн. концепцию совр. теории сверхпроводимости - наличие единой волновой функции и фазовой когерентности спаренных электронов в сверхпроводящем состоянии. По своей доступности эксперим. исследованию Д. э. представляет собой одну из уникальных возможностей изучать проявления квантовых свойств микромира в макроскопич. масштабе.

Д. э. используют в целом ряде криогенных приборов. Соотношение (1) является основой практич. использования стационарного Д. э. в т. н. сверхпроводящих квантовых интерферометрах (сквидах). ДК могут применяться в качестве генераторов и -детекторов СВЧ-диапазона. Свойство ДК переключаться с нулевого на конечное напряжение при превышении током критич. значения в совокупности с малой ёмкостью позволяет использовать их в качестве быстродействующих логич. элементов ЭВМ [7, 8]. Соотношение (4) может использоваться для уточнения фундаментальных физических констант и создания стандартов напряжения. На основе Д. э. совр. методами измерено отношение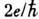

=4,83594000*10¹⁴ Гц/В с погрешностью 2*10^-8, что позволяет создать стандарт вольта с погрешностью ~10^-9.

Литература по Джозефсона эффекту

Знаете ли Вы, в чем ложность понятия "физический вакуум"?

Физический вакуум - понятие релятивистской квантовой физики, под ним там понимают низшее (основное) энергетическое состояние квантованного поля, обладающее нулевыми импульсом, моментом импульса и другими квантовыми числами. Физическим вакуумом релятивистские теоретики называют полностью лишённое вещества пространство, заполненное неизмеряемым, а значит, лишь воображаемым полем. Такое состояние по мнению релятивистов не является абсолютной пустотой, но пространством, заполненным некими фантомными (виртуальными) частицами. Релятивистская квантовая теория поля утверждает, что, в согласии с принципом неопределённости Гейзенберга, в физическом вакууме постоянно рождаются и исчезают виртуальные, то есть кажущиеся (кому кажущиеся?), частицы: происходят так называемые нулевые колебания полей. Виртуальные частицы физического вакуума, а следовательно, он сам, по определению не имеют системы отсчета, так как в противном случае нарушался бы принцип относительности Эйнштейна, на котором основывается теория относительности (то есть стала бы возможной абсолютная система измерения с отсчетом от частиц физического вакуума, что в свою очередь однозначно опровергло бы принцип относительности, на котором постороена СТО). Таким образом, физический вакуум и его частицы не есть элементы физического мира, но лишь элементы теории относительности, которые существуют не в реальном мире, но лишь в релятивистских формулах, нарушая при этом принцип причинности (возникают и исчезают беспричинно), принцип объективности (виртуальные частицы можно считать в зависимсоти от желания теоретика либо существующими, либо не существующими), принцип фактической измеримости (не наблюдаемы, не имеют своей ИСО).

Когда тот или иной физик использует понятие "физический вакуум", он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.

Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик Анри Пуанкаре, уже нельзя. Слишком много фактов противоречит этому.

Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование "моря" двух компенсирующих друг друга энергий в вакууме - положительной и отрицательной, а также "моря" компенсирующих друг друга частиц - виртуальных (то есть кажущихся) электронов и позитронов в вакууме.

Однако такая постановка является внутренне противоречивой (виртуальные частицы ненаблюдаемы и их по произволу можно считать в одном случае отсутствующими, а в другом - присутствующими) и противоречащей релятивизму (то есть отрицанию эфира, так как при наличии таких частиц в вакууме релятивизм уже просто невозможен). Подробнее читайте в FAQ по эфирной физике.