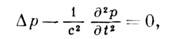
а при известном р можно определить остальные характеристики 3. п. по ф-лам:
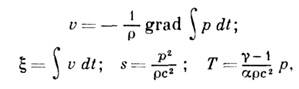
где с - скорость звука, g=cp/cV - отношение теплоёмкости при пост. давлении к теплоёмкости при пост. объёме, а - коэф. теплового расширения среды. Для гармонич. 3. п. волновое ур-ние переходит в ур-ние Гельмгольца: Dр+k2р = 0, где k=w/c - волновое число для частоты w, а выражения для v и x принимают вид:
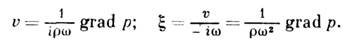
Кроме того, 3. п. должно удовлетворять граничным условиям, т. е. требованиям, к-рые налагают на величины, характеризующие 3. п., физ. свойства границ - поверхностей, ограничивающих среду, поверхностей, ограничивающих помещённые в среду препятствия, и поверхностей раздела разл. сред. Напр., на абсолютно жёсткой границе нормальная компонента колебат. скорости vn должна обращаться в нуль; на свободной поверхности должно обращаться в нуль звуковое давление; на границе, характеризующейся импедансом акустическим, p/vn должно равняться удельному акустич. импедансу границы; на поверхности раздела двух сред величины р и vn по обе стороны от поверхности должны быть попарно равны. В реальных жидкостях и газах имеется дополнит. граничное условие: обращение в нуль касательной компоненты колебат. скорости на жёсткой границе или равенство касательных компонент на поверхности раздела двух сред. В твёрдых телах внутр. напряжения характеризуются не давлением, а тензором напряжений, что отражает наличие упругости среды по отношению к изменению не только её объёма (как в жидкостях и газах), но и формы. Соответственно усложняются и ур-ния 3. п., и граничные условия. Ещё более сложны ур-ния для анизотропных сред. Ур-ния 3. п. и граничные условия отнюдь не определяют сами по себе вид волн: в разл. ситуациях в той же среде при тех же граничных условиях 3. п. будут иметь разный вид. Ниже описаны разные виды 3. п., возникающие в разл. ситуациях. 1) Свободные волны - 3. п., к-рое может существовать во всей неогранич. среде в отсутствие внеш. воздействий, напр., плоские волны p=p(x6ct), бегущие вдоль оси х в положительном (знак "-") и отрицательном (знак "+") направлениях. В плоской волне p/v = brс, где rс - волновое сопротивление среды. В местах положит. звукового давления направление колебат. скорости в бегущей волне совпадает с направлением распространения волны, в местах отрицат. давления - противоположно этому направлению, а в местах обращения давления в нуль колебат. скорость также обращается в нуль. Гармонич. плоская бегущая волна имеет вид: p=p0cos(wt-kx+j), где р0 и j0 - соответственно амплитуда волны и её нач. фаза в точке х=0. В средах с дисперсией скорости звука скорость гармонич. волны с=w/k зависит от частоты. 2) Колебания в огранич. областях среды в отсутствие внеш. воздействий, напр. 3. п., возникающее в замкнутом объёме при заданных нач. условиях. Такие 3. п. можно представить в виде суперпозиции стоячих волн, характерных для данного объёма среды. 3) 3. п., возникающие в неогранич. среде при заданных нач. условиях - значениях р и v в нек-рый нач. момент времени (напр., 3. п., возникающие после взрыва). 4) 3. п. излучения, создаваемые колеблющимися телами, струями жидкости или газа, захлопывающимися пузырьками и др. естеств. или искусств. акустич. излучателями (см. Излучение звука ).Простейшими по форме поля излучениями являются следующие. Монопольное излучение - сферически симметричная расходящаяся волна; для гармонич. излучения она имеет вид: р = -irwQехр (ikr)/4pr, где Q - производительность источника (напр., скорость изменения объёма пульсирующего тела, малого по сравнению с длиной волны), помещённого в центр волны, а r - расстояние от центра. Амплитуда звукового давления при монопольном излучении изменяется с расстоянием как 1/r, а
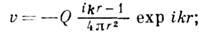
в неволновой зоне (kr<<1) v изменяется с расстоянием как 1/r2, а в волновой (kr>>1) - как 1/r. Сдвиг фаз j между р и v монотонно убывает от 90° в центре волны до нуля на бесконечности; tg j=1/kr. Дипольное излучение - сферич. расходящаяся волна с "восьмёрочной" характеристикой направленности вида:
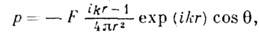
где F - сила, приложенная к среде в центре волны, q - угол между направлением силы и направлением на точку наблюдения. Такое же излучение создаётся сферой радиуса a<<l (l - длина волны), помещённой в центр волны и осциллирующей со скоростью u=F/2prwa3. Поршневое излучение - 3. п., создаваемые поступательными колебаниями плоского поршня. Если его размеры >>l, то излучение представляет собой квазиплоскую волну, распространяющуюся в виде огранич. пучка, опирающегося на поршень. По мере удаления от поршня дифракция размывает пучок, переходящий на большом расстоянии от поршня в многолепестковую расходящуюся сферич. волну. Все виды 3. п. излучения на большом расстоянии от излучателя (в т. н. дальней зоне, или зоне Фраунгофера) асимптотически принимают вид расходящихся сферич. волн: р=Aехр (ikr)R (q, j)/r, где А -постоянная, q и j - углы сферич. системы координат, R (q, j) - характеристика направленности излучения. Т.о., асимптотически поле убывает обратно пропорционально расстоянию точки наблюдения от области расположения источника звука. Началом дальней зоны обычно считают расстояние r=D2/l, где D - поперечные размеры излучающей системы. В т. н. ближней зоне (френелевская зона) для 3. п. излучения в общем случае нет к--л. определённой зависимости от r, а угл. зависимость меняется при изменении r - характеристика направленности ещё не сформирована. 5) 3. п. фокусировки - поля вблизи фокусов и каустик фокусирующих устройств, характеризующиеся повыш. значениями звукового давления, обращающегося (при пользовании приближениями геом. акустики) в бесконечность в фокусах и на каустиках (см. Фокусировка звука). 6) 3. п., связанные с наличием в среде ограничивающих поверхностей и препятствий. При отражении и преломлении плоских волн на плоских границах возникают также плоские отражённые и преломлённые волны. В волноводах акустических, заполненных однородной средой, суперпозиция плоских волн образует нормальные волны. При отражении гармонич. плоских волн от плоских границ образуются стоячие волны, причём результирующие поля могут оказаться стоячими в одном направлении и бегущими - в другом. 7) 3. п., затухающие вследствие неидеальности среды - наличия вязкости, теплопроводности и т. п. (см. Поглощение звука ).Для бегущих волн влияние такого затухания характеризуют множителем ехр aх, где a - амплитудный пространственный коэф. затухания, связанный с добротностью Q среды соотношением: a=k/2Q. В стоячих волнах появляется множитель ехр (-dt), где d = сa=w/2Q - амплитудный временной коэф. затухания звука.
Измерение параметров 3. п. производят разл. приёмниками звука: микрофонами - для воздуха, гидрофонами - для воды. При исследовании тонкой структуры 3. п. следует пользоваться приёмниками, размеры к-рых малы по сравнению с длиной волны звука. Визуализация звуковых полей возможна путём наблюдения дифракции света на ультразвуке, методом Теплера (теневой метод ),методом электронно-оптич. преобразования и др.

