Геометрическая акустика. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Геометрическая акустика - упрощённая теория распространения звука, пренебрегающая дифракц. явлениями (см. Дифракция волн, Дифракция звука). В геометрической акустике звуковое поле представляют в виде лучевой картины, не зависящей от длины волны, и считают, что звуковая энергия распространяется вдоль каждой лучевой трубки независимо от остальных лучей; это даёт обратную пропорциональность между плотностью потока энергии вдоль луча и площадью поперечного сечения лучевой трубки. В однородных средах лучи - прямые линии, в неоднородных они искривляются (см. Рефракция звука).

С матем. точки зрения геометрической акустики есть предельный случай волновой теории распространения звука при стремлении длины волны к нулю и в этом отношении аналогична геометрической оптике в теории распространения света. Геометрической акустикой можно пользоваться при конечной длине волны звука, если эта длина достаточно мала по сравнению с расстоянием, на к-ром скорость звука меняется существенно, и по сравнению с характерными размерами задачи (напр., размерами препятствия, поперечником излучателя и т. п.); кроме того, должно быть выполнено условие медленности изменения параметров звукового поля в направлении, перпендикулярном к лучам. Геометрическая акустика неприменима или даёт значит. погрешность при расчёте звукового поля в областях, где вследствие волновой природы звука существенны дифракц. эффекты, к-рые в геометрической акустике не учитываются принципиально (напр., вблизи границы тени, вблизи фокальной области при фокусировке звука и т. п.). В области применимости геометрической акустики звуковое поле в любой точке можно рассматривать локально как квазиплоскую волну, бегущую в направлении касательной к лучу. Для гармонич. волн каждую величину р, характеризующую поле, можно записать в виде

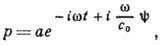
где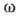

- частота, амплитуда а - медленно меняющаяся функция координат, с₀ - локальная скорость звука в нач. точке, а эйконал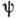

связан с локальным коэф. преломления п соотношением

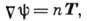
где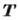

- единичный вектор касательной к лучу. Пользуясь Ферма принципом ,можно найти ур-ние луча в виде

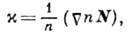
где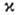

- кривизна луча, N - единичный вектор его гл. нормали. Из этого ур-ния следует, что луч искривляется в сторону уменьшения скорости звука.

При распространении звука соотношения геометрической акустики могут потерять свою применимость в результате усложнения структуры звукового поля, а затем вновь восстановить её. Так, при приближении к каустической поверхности геометрическая акустика даёт при расчёте поля ошибочные результаты (в частности, согласно лучевой картине, поле на каустике обращается в бесконечность); по удалении от каустики звуковое поле снова правильно описывается лучевой картиной. При физ. выделении лучевой трубки, напр. при диафрагировании плоской волны большим отверстием в экране, когда, согласно геометрической акустике, проходящий пучок параллельных лучей должен был бы распространяться неограниченно, в действительности лучи постепенно вытесняются с боков дифракц. полем и на расстоянии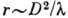

от экрана (D - линейный размер отверстия,

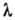- длина волны звука) проходящее поле полностью теряет свой лучевой характер. При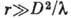

лучевой характер поля восстанавливается, но получающийся пучок лучей оказывается расходящимся. Аналогично ведёт себя пучок лучей, создаваемый большим поршневым излучателем. Звуковая тень позади большого препятствия засвечивается с боков дифракц. полем, огибающим препятствие. Вдали от источников звука и от препятствий звуковое поле в среде со свойствами, медленно меняющимися от точки к точке, описывается лучевой картиной всюду, за исключением областей, близких к каустикам. Действие линз акустических и зеркал акустических можно изучать при помощи геометрической акустики всюду, за исключением области, близкой к фокусу.

Отражение и преломление звука можно рассматривать при помощи лучевой картины при условии, что радиусы кривизны граничной поверхности велики по сравнению с длиной волны, а источник звука находится вдали от границы. Направления отражённых и преломленных лучей следует определять по Снелля закону ,считая, что отражение происходит в каждой точке от плоскости, касательной к поверхности в этой точке; амплитуды отражённого и преломлённого луча определяются по ф-лам Френеля для отражения и преломления плоских волн.

Геометрическая акустика широко применяют при расчёте звуковых полей в естественных средах: в атмосфере, океане и толще Земли (особенно при распространении на большие расстояния). Лучевая картина позволяет объяснить образование звуковых теней, зон молчания, зон аномальной слышимости, явление сверхдальнего распространения в подводном звуковом канале и т. п. и делается неприменимой только на низком инфразвуке (см. Гидроакустика, Геоакустика).

Литература по геометрической акустике

Знаете ли Вы, что такое "усталость света"?
Усталость света, анг. tired light - это явление потери энергии квантом электромагнитного излучения при прохождении космических расстояний, то же самое, что эффект красного смещения спектра далеких галактик, обнаруженный Эдвином Хабблом в 1926 г.
На самом деле кванты света, проходя миллиарды световых лет, отдают свою энергию эфиру, "пустому пространству", так как он является реальной физической средой - носителем электромагнитных колебаний с ненулевой вязкостью или трением, и, следовательно, колебания в этой среде должны затухать с расходом энергии на трение. Трение это чрезвычайно мало, а потому эффект "старения света" или "красное смещение Хаббла" обнаруживается лишь на межгалактических расстояниях.
Таким образом, свет далеких звезд не суммируется со светом ближних. Далекие звезды становятся красными, а совсем далекие уходят в радиодиапазон и перестают быть видимыми вообще. Это реально наблюдаемое явление астрономии глубокого космоса. Подробнее читайте в FAQ по эфирной физике.