 -лучей.
Интерпретация А. п. э. предложена М. фон Лауэ (М. von Laue) в 1949. Обычно интенсивность
рентг. лучей при распространении в кристалле экспоненциально уменьшается с глубиной
z проникновения излучения в кристалл:
-лучей.
Интерпретация А. п. э. предложена М. фон Лауэ (М. von Laue) в 1949. Обычно интенсивность
рентг. лучей при распространении в кристалле экспоненциально уменьшается с глубиной
z проникновения излучения в кристалл: АНОМАЛЬНОГО ПРОПУСКАНИЯ ЭФФЕКТ - резкое
уменьшение поглощения части потока излучения в толстом идеальном кристалле при
лауэвском пропускании. А. п. э. впервые наблюдался X. Борманом в 1941 для рентг.
лучей (эффект Бормана), позднее исследован для нейтронов, электронов и  -лучей.
Интерпретация А. п. э. предложена М. фон Лауэ (М. von Laue) в 1949. Обычно интенсивность
рентг. лучей при распространении в кристалле экспоненциально уменьшается с глубиной
z проникновения излучения в кристалл:
-лучей.
Интерпретация А. п. э. предложена М. фон Лауэ (М. von Laue) в 1949. Обычно интенсивность
рентг. лучей при распространении в кристалле экспоненциально уменьшается с глубиной
z проникновения излучения в кристалл:
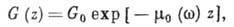 (1)
(1)
где G0 - интенсивность первичного
поля; z - координата вдоль направления распространения;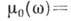
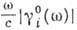 - линейный коэфф. фотоэлектрич. поглощения среды;
- линейный коэфф. фотоэлектрич. поглощения среды; 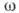 - частота излучения;
- частота излучения;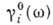 -
мнимая часть нулевой фурье-компоненты рентгеновской поляризуемости.
-
мнимая часть нулевой фурье-компоненты рентгеновской поляризуемости.
Зависимость (1) предполагает пространственную
однородность поля излучения в кристалле или нерегулярное строение (искажение)
кристалла и правильно описывает ослабление интенсивности излучения при его распространении
в кристалле в произвольном (не дифракционном) направлении. Она также верна и
при кинематич. дифракции рентгеновских лучей в тонком (по сравнению с
длиной первичной экстинкции)кристалле. Если толщина кристалла 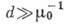 , то, согласно (1), излучение полностью поглощается в нём.
, то, согласно (1), излучение полностью поглощается в нём.
При динамич. дифракции в условиях лауэвского
пропускания значит. часть интенсивности поля проходит через толстые  кристаллы, практически не ослабляясь. Это явление и наз. А. п. э. При динамич.
дифракции в кристалле устанавливается пространственно-неоднородная структура
поля с масштабом неоднородности порядка размеров элементарной ячейки кристалла.
Для правильного описания ослабления интенсивности такого поля показатель экспоненты
в (1) должен учитывать не только величину фотоэлектрического поглощения, но
и пространственную структуру поля.
кристаллы, практически не ослабляясь. Это явление и наз. А. п. э. При динамич.
дифракции в кристалле устанавливается пространственно-неоднородная структура
поля с масштабом неоднородности порядка размеров элементарной ячейки кристалла.
Для правильного описания ослабления интенсивности такого поля показатель экспоненты
в (1) должен учитывать не только величину фотоэлектрического поглощения, но
и пространственную структуру поля.
Наиб. благоприятным для наблюдения А.
п. э. случаем является симметричное лауэвское пропускание s-поляризов. излучения
при точном выполнении Брэгга-Вульфа условия. При этом отражающие атомные
плоскости перпендикулярны входной поверхности кристаллич. пластины, а вектор
дифракции g параллелен ей.
Рассмотрим А. п. э. для случая, когда
имеется лишь 2 луча - один проходящий и один дифракционный (см. рис. 1 к ст.
Дисперсионная поверхность] .Согласно динамич. теории дифракции, поле
в кристалле в этом случае для каждой из двух (s и р)поляризаций (см.
Поляризация света)состоит из четырёх волн, попарно принадлежащих разным
листам дисперсионной поверхности, описывающей зависимость волнового вектора
от частоты излучения. Если кристаллографич. плоскости центросимметричного кристалла
при точном выполнении Брэгга - Вульфа условия перпендикулярны поверхности кристалла,
то суммарная индукция элек-трич. поля эл--магн. волны для каждого листа дисперсионной
поверхности будет равна
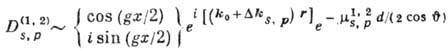 ,(1)
,(1)
где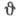 -угол
Брэгга,
-угол
Брэгга,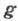 -вектор
обратной кристаллической решётки,
-вектор
обратной кристаллической решётки,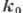 ''. - волновой вектор первичной волны,
''. - волновой вектор первичной волны,
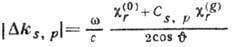 - добавка к z-компоненте вектора
к0 за счёт преломления,
- добавка к z-компоненте вектора
к0 за счёт преломления, 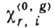 -действительная (r) и мнимая (i) части фурье-компонент рентг.
поляризуемости, Cs = 1,
-действительная (r) и мнимая (i) части фурье-компонент рентг.
поляризуемости, Cs = 1, 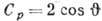 ;
линейные коэффициенты поглощения
;
линейные коэффициенты поглощения 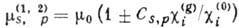 ,
где
,
где 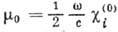 .
.
Члены 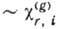 в выражении для
в выражении для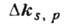 и
и 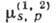 описывают влияние интерференции на преломление и поглощение излучения при дифракции.
Для s-поляризации из-за слабой зависимости
описывают влияние интерференции на преломление и поглощение излучения при дифракции.
Для s-поляризации из-за слабой зависимости 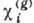 от
от 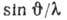 отношение
отношение 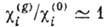 ,
так что
,
так что 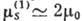 , а
, а 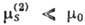 .
Следовательно, излучение с Ds(1)' поглощается сильнее, а с Ds(2)-слабее,
чем в произвольном направлении. Поэтому через кристалл толщиной
.
Следовательно, излучение с Ds(1)' поглощается сильнее, а с Ds(2)-слабее,
чем в произвольном направлении. Поэтому через кристалл толщиной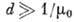 может проходить только излучение с Ds(2).
может проходить только излучение с Ds(2).
Прошедшее излучение имеет преимущественную
s-поляризацию, так как для р-поляризации 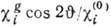 < 1 и А. п. э. выражен слабее. А. п. э. существует во всей угловой области
дифракционного отражения, однако при увеличении отстройки
< 1 и А. п. э. выражен слабее. А. п. э. существует во всей угловой области
дифракционного отражения, однако при увеличении отстройки 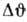 от точного угла Брэгга
от точного угла Брэгга 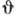 он быстро ослабляется.
он быстро ослабляется.
Пойнтинга векторы полей 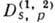 в соответствии с (1) равны:
в соответствии с (1) равны:
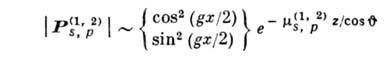 (2)
(2)
и направлены вдоль атомных плоскостей,
а их амплитуды в направлении, перпендикулярном атомным плоскостям, модулированы
с периодом, равным межплоскостному расстоянию. Вследствие этого 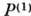 принимает макс. значения на атомных плоскостях, а
принимает макс. значения на атомных плоскостях, а 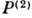 - между ними (рис.).
- между ними (рис.).
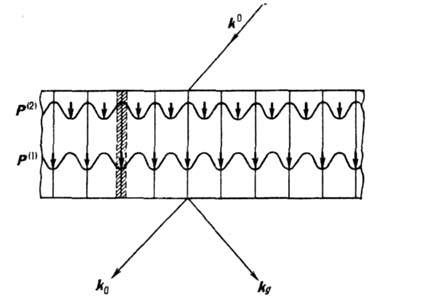
Картина распределения вектора Пойнтинга
для полей D(1) и D(2) в совершенном кристалле, атомные
плоскости которого перпендикулярны поверхности, при точном выполнении условий
Брэгга - Вульфа. 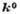 - волновой вектор падающей плоской волны. Потоки энергии направлены вдоль атомных
плоскостей и модулированы в направлении оси х так, что для поля D(1)
максимумы интенсивности приходятся на атомные плоскости (и поэтому они сильно
поглощаются его атомами), а для поля D(2)- между ними (коэффициент
поглощения аномально мал). Поскольку потоки энергии направлены вдоль атомные
плоскостей, то разделение поля на прошедшую и дифракционную волны происходит
при выходе его из кристалла. Пунктиром показано влияние несовершенства структуры
кристалла и тепловых колебаний, которые ведут к эффективному увеличению толщины
(заштрихованные области) атомной плоскости и, следовательно, сглаживанию эффекта
аномального прохождения.
- волновой вектор падающей плоской волны. Потоки энергии направлены вдоль атомных
плоскостей и модулированы в направлении оси х так, что для поля D(1)
максимумы интенсивности приходятся на атомные плоскости (и поэтому они сильно
поглощаются его атомами), а для поля D(2)- между ними (коэффициент
поглощения аномально мал). Поскольку потоки энергии направлены вдоль атомные
плоскостей, то разделение поля на прошедшую и дифракционную волны происходит
при выходе его из кристалла. Пунктиром показано влияние несовершенства структуры
кристалла и тепловых колебаний, которые ведут к эффективному увеличению толщины
(заштрихованные области) атомной плоскости и, следовательно, сглаживанию эффекта
аномального прохождения.
Т. к. осн. вклад в фотоэлектрич. поглощение
дают внутр. К- и L-оболочки, электронная плотность к-рых
сосредоточена вблизи атомных ядер, поле D(1) распространяется
в области повышенной электронной плотности, взаимодействует со средой и поглощается
более интенсивно, а поле D(2) распространяется в области пониженной
электронной плотности и взаимодействует со средой менее интенсивно, чем в произвольном,
не дифракционном направлении. Этим и обусловлены аномально низкое поглощение
в дифракц. направлении и появление резких максимумов на рентгенограмме. Тепловые
колебания атомов в кристалле эффективно увеличивают размеры атомов, так что
m(2)s,p
возрастает. Напр., при температуре 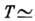 300К
300К
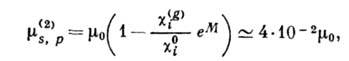
где 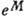 -
Дебая-Валлера фактор. А. п. э. зависит также от структуры кристалла. Любые отклонения
от идеальных условий (атомные плоскости не перпендикулярны кристаллографич.
плоскостям, наличие отстройки от точного угла
-
Дебая-Валлера фактор. А. п. э. зависит также от структуры кристалла. Любые отклонения
от идеальных условий (атомные плоскости не перпендикулярны кристаллографич.
плоскостям, наличие отстройки от точного угла 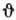 ,
дефектов) уменьшают А. п. э. При многолучевой дифракции могут существовать области,
где А. п. э. проявляется ещё сильнее.
,
дефектов) уменьшают А. п. э. При многолучевой дифракции могут существовать области,
где А. п. э. проявляется ещё сильнее.
А. п. э. используется для исследования
совершенства строения кристаллов (см. Рентгеновская топография)и получения
слаборасходящихся пучков монохроматич. поляризов. рентг. излучения. А. п. э.
имеет место и для др. излучений.

|
|