к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

РЕАЛЬНАЯ ФИЗИКА

Глоссарий по физике

А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

Дисперсионная поверхность

Дисперсионная поверхность - поверхность равных частот в пространстве волновых векторов. Характеризует пространств. дисперсию фазовой скорости дифракц. рентг. волн в кристалле в зависимости от отклонения направления распространения первичного излучения от направления, соответствующего Брэгга - Вульфа условию. Понятие Д. п. широко используется в динамич. теории дифракции рентг. лучей в кристаллах. Конкретный вид Д. п. зависит от числа дифракц. волн, реального строения кристалла и др. факторов. Понятие Д. п. естеств. образом возникает при решении волнового ур-ния, описывающего распространение рентг. лучей в кристаллах [см. ур-ние (5) в ст. Дифракция рентгеновских лучей]. Решения этого ур-ния в нулевом приближении (т. е. без учёта взаимодействия волн в кристалле) показывают, что волновые векторы всех волн равны между собой:

где k_g и k₀ - абс. значения волновых векторов соответственно дифракционной и проходящей волн. Согласно (1), Д. п. состоит из бесконечного числа сфер радиуса k₀, проведённых вокруг каждого узла обратной решётки кристалла (рис. 1). Направления волновых векторов k_g при этом не определяются.

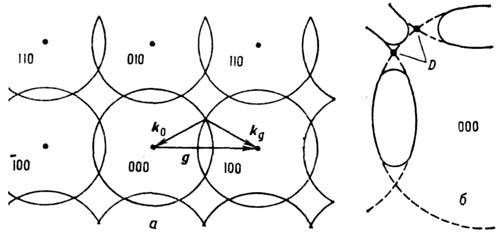
Рис. 1. а - Сечение дисперсионных поверхностей нулевого приближения плоскостью обратной решётки. В кинематическом приближении волновые векторы k₀ и k_g выходят из точек пересечения (вырождения) дисперсионной поверхности узла g [на рис. это узел (100)] обратной решетки с дисперсионной поверхностью нулевого узла (000) обратной решётки; б - фрагмент сечения дисперсионной поверхности плоскостью рисунка согласно динамической теории. Пунктиром показаны участки сечения дисперсионной поверхности до снятия вырождения; D - точки вырождения.

В первом, т. н. кинематическом, приближении, к-рое учитывает только одностороннее влияние проходящей волны на дифракционные, к (1) добавляется условие Брэгга - Вульфа:

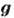( - вектор обратной решётки), к-рое однозначно задаёт направление распространения дифракц. волн. Согласно условиям (1) и (2), волновые векторы дифракционных волн должны начинаться в тех точках обратного пространства, к-рые одновременно принадлежат нулевой сфере и сфере g (рис. 1). Это возможно только при 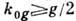, когда соответствующая узлу g сфера пересекается с нулевой сферой. Тем самым условия (1) и (2) полностью определяют число и направления распространения возможных при данных условиях дифракц. волн (построение Эвальда). Для бесконечно большого кристалла Д. п. вырождается в окружности, являющиеся следами пересечения сфер, в каждой точке к-рых условия (1) и (2) выполняются точно.

Узлы обратной решётки конечного кристалла также имеют конечные размеры. Совокупность сфер, проведённых радиусом k₀ из каждой точки данного узла, образует оболочку конечной толщины. Пересечение оболочек представляет собой уже нек-рую трёхмерную область, внутри к-рой условие (1) выполняется приближённо в конечном интервале углов (частот). Это означает, что дифракц. максимумы всегда имеют конечную угловую (частотную) ширину.

Динамич. теория дифракции последовательно учитывает взаимодействие между всеми волнами в кристалле. Учёт этого взаимодействия приводит к расщеплению Д. п. (снятию вырождения) вдоль линий пересечения сфер (линии вырождения). В результате этого структура Д. п. становится существенно более сложной. В двухлучевом случае, напр., сечение Д. п. вблизи точки вырождения плоскостью рисунка имеет вид гипербол (рис. 2). Д. п. в непосредств. окрестности линии вырождения получается вращением гипербол вокруг вектора 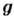. Миним. величина расщепления (расстояние между вершинами гипербол) прямо пропорциональна дифракц. фурье-компонентам поляризуемости рентгеновской.

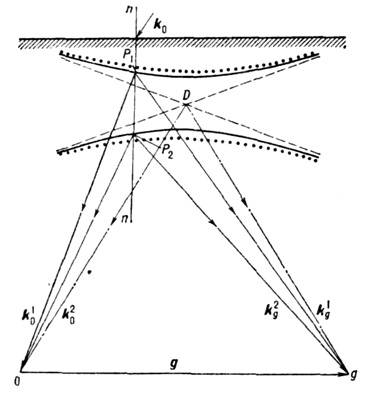
Рис. 2. Сечение дисперсионной поверхности плоскостью рисунка вблизи точки вырождения в симметричном двухлучевом лауэвском прохождении при нек-ром отклонении угла скольжения первичного луча с волновым вектором k₀ от угла Брэгга, n- нормаль к поверхности кристалла; отражающая система атомных плоскостей перпендикулярна поверхности кристалла и плоскости рисунка; P₁ и P₂ - центры распространения на сечениях листов дисперсионной поверхности для р-поляризованвого излучения; пунктирными линиями показаны дисперсионные поверхности для s-поляризованного излучения, штриховыми - поверхности в кинематическом приближении, штрих-пунктирными - волновые векторы проходящей k₀ и дифракционной k_g волн в кинематическом приближении согласно (1, 2). Положение центров распространения P₁ и P₂ на дисперсионной поверхности определяет величины и направления волновых векторов проходящих 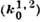и дифракционных 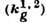волн. При увеличении (уменьшении) угла скольжения P₁ и P₂ смещаются влево (вправо) по дисперсионной поверхности.

Фазовые скорости s- и р-поляризованных по отношению к плоскости падения волн различны. Поэтому в общем случае неполяризов. излучения Д. п. состоит из четырёх листов - по два для каждой поляризации, а в кристалле распространяются восемь волн: по четыре в прямом и дифракционном направлениях. Интерференц. взаимодействие этих волн между собой обусловливает особенности динамич. дифракции. Вообще, если в кристалле одновременно распространяется n лучей, то Д. п. имеет 2n листов, и всего в кристалле возникает 2n² волн.

Точки Д. п., из к-рых выходят волновые векторы, наз. центрами распространения. Для однозначной фиксации на Д. п. положения центров распространения используются условия непрерывности тангенциальных компонент волновых векторов на границе кристалла. Если направление падения первичного луча на кристалл изменяется, то центры распространения перемещаются по Д. п. (рис. 2). При этом для удовлетворения условию дифракции (2) длины волновых векторов k₀ и k_g изменяются, что обеспечивается резкой пространственной дисперсией фазовой скорости волн в узком угловом (частотном) интервале вблизи угла Брэгга. Важное свойство Д. п. состоит в том, что Пойнтинга вектор для каждой пары волн (в двухлучевом случае), исходящих из одного центра распространения, перпендикулярен касательной к Д. п. в центре распространения.

Д. п. можно также вести и для искажённых кристаллов.

Лит. см. при ст. Дифракция рентгеновских лучей.

Литература по дисперсионным поверхностям

Джеймс Р., Оптические принципы дифракции рентгеновских лучей, пер. с англ., M., 1950;
Жданов Г. С., Основы рентгеновского структурного анализа, M.- Л., 1940;
Гинье А., Рентгенография кристаллов, пер. с франц., M., 1961;
Порай-Кошиц M. А., Практический курс рентгеноструктурного анализа, т. 2, M., 1960;
Иверонова В. И., Ревкевич Г. П., Теория рассеяния рентгеновских лучей, 2 изд., M., 1978;
Скрышевский А. Ф., Структурный анализ жидкостей и аморфных тел, 2 изд., M., 1980;
Кривоглаз M. А., Дифракция рентгеновских лучей и нейтронов в неидеальных кристаллах, К., 1983;
Амелинкс С., Методы прямого наблюдения дислокаций [кристаллов], пер. с англ., M., 1968;
Афанасьев A. M., Александров П. А., Имамов P.M., Рентгеновская структурная диагностика в исследовании приповерхностных слоев монокристаллов, M., 1986;
Беляков В. А., Сонин А. С., Оптика холестерических жидких кристаллов, M., 1982;
Пинскер З. Г., Рентгеновская кристаллооптика, M., 1982.

А. В. Колпаков.

к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

Знаете ли Вы, что в 1974 - 1980 годах профессор Стефан Маринов из г. Грац, Австрия, проделал серию экспериментов, в которых показал, что Земля движется по отношению к некоторой космической системе отсчета со скоростью 360±30 км/с, которая явно имеет какой-то абсолютный статус. Естественно, ему не давали нигде выступать и он вынужден был начать выпуск своего научного журнала "Deutsche Physik", где объяснял открытое им явление. Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМА

Рыцари теории эфира