Цилиндрическая волна - волна, радиально расходящаяся от или сходящаяся к нек-рой оси в пространстве или точке на плоскости.
В последнем случае эти волны наз. также круговыми. Примерами Ц. в. могут служить
волны на поверхности воды от брошенного камня или колеблющегося поплавка, эл--магн.
или акустич. волны, возбуждаемые источниками, расположенными в пространстве,
ограниченном, напр., двумя плоскопараллельными отражателями (в т. ч. внутри
океанич. волноводов и т. д.).
Структура Ц. в. существенно сложнее структуры
плоских (одномерных) и сферич. (трёхмерных) волн. Простейшая монохроматич. симметричная
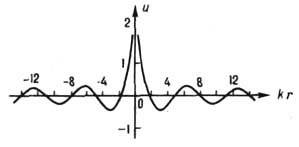
Ц. в. с источником в центре (рис. 1) удовлетворяет двумерному волновому уравнению и описывается с помощью функции Ханкеля нулевого порядка H0(kr):
Рис. 1. Радиально расходящаяся цилиндрическая
волна, возбуждаемая источником в
центре.
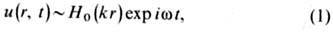
где w - круговая частота, k - волновое
число. На больших расстояниях от оси (kr >> 1) волновое поле (1)
приобретает вид
и только в этом асимптотич. представлении в Ц.
в. можно однозначно выделить амплитуду А/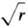
и фазу wt - kr = w(t
-r/uф),
где фазовая скорость uф
совпадает с фазовой скоростью плоской волны: uф
= w/k = 2p/l (l - длина волны). По мере удаления
от оси квадрат модуля волнового возмущения (2) убывает как 1/r, а поверхность
цилиндра, охватывающая источник, растёт пропорционально r, так что, в
соответствии с законом сохранения энергии, суммарное значение потока энергии,
уносимого от источника на оси, остаётся постоянным.
В отсутствие дисперсии волн из гармонич.
волн (2) вдали от оси можно составить волну любой формы (в частности, уединённую
волну или волновой пакет), перемещающуюся с пост. скоростью uф=u:
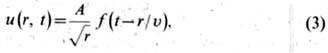
где функция f(t - r/u)удовлетворяет одномерному волновому ур-нию. Однако в промежуточной области,
где kr~1, даже в среде без дисперсии происходит сильная деформация
волнового возмущения (рис. 2).
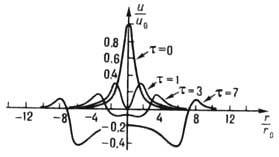
Рис. 2. Радиально расходящаяся цилиндрическая
волна, заданная в начальный момент
времени в форме одиночного импульса
u = u0(1+ r/r0)3/2.
С увеличением t
=ct/r0 (с ростом
времени t)импульс расплывается, оставляя за собой
"шлейф".
Это связано с тем, что Ц. в. в принципе нестационарна:
удаляясь от оси (центра), она оставляет за собой "шлейф", к-рый
можно интерпретировать как результат прихода волновых возмущений от всё более
и более удалённых от точки наблюдения источников на оси.
Лит. см. при ст. Волны. M. А. Миллер,
Л. А. Островский.
|
|
 |
