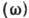 и волновых векторов
(k). B случае одного пространственного измерения (х)и скалярного
комплексного волнового поля В. п.
и волновых векторов
(k). B случае одного пространственного измерения (х)и скалярного
комплексного волнового поля В. п. 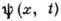 можно представить в виде интеграла Фурье:
можно представить в виде интеграла Фурье:Волновой пакет - волновое образование из колебаний произвольной природы, представляющее собой
суперпозицию (наложение) плоских монохроматич. волн с близкими значениями частот
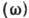 и волновых векторов
(k). B случае одного пространственного измерения (х)и скалярного
комплексного волнового поля В. п.
и волновых векторов
(k). B случае одного пространственного измерения (х)и скалярного
комплексного волнового поля В. п. 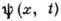 можно представить в виде интеграла Фурье:
можно представить в виде интеграла Фурье:
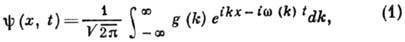
где g (k)заметно
отлично от нуля лишь для значений k, лежащих внутри интервала 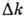 вблизи нек-рого k=k0. В отличие от плоской монохроматич. волны,
существующей во всем пространстве, В. п. занимает конечную часть пространства,
т. к. из (1) следует:
вблизи нек-рого k=k0. В отличие от плоской монохроматич. волны,
существующей во всем пространстве, В. п. занимает конечную часть пространства,
т. к. из (1) следует:

Разброс 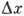 по координатам функции
по координатам функции 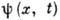 (ширина пакета) скоррелирован с разбросом Dk функции g(k)по волновым
числам k:
(ширина пакета) скоррелирован с разбросом Dk функции g(k)по волновым
числам k:

Под разбросом (шириной)
величины 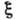 понимается
среднеквадратичное
отклонение
понимается
среднеквадратичное
отклонение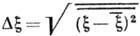 .
Эволюция В. п. (1) предопределена, если известны g (k)и закон дисперсии
волн-связь
.
Эволюция В. п. (1) предопределена, если известны g (k)и закон дисперсии
волн-связь 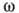 и k:
и k:

Если эта связь линейна,
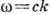 , где с=const
(как в случае световых волн в пустоте), то
, где с=const
(как в случае световых волн в пустоте), то
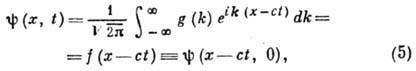
т. е. В. п. распространяется
со скоростью с без изменения своей формы.
В общем случае произвольной
связи 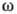 и k зависимость
и k зависимость 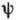 от х и t имеет более сложный вид, и характер распространения В.
п. может быть описан следующим усредненным (интегральным) соотношением:
от х и t имеет более сложный вид, и характер распространения В.
п. может быть описан следующим усредненным (интегральным) соотношением:
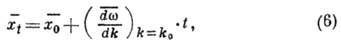
описывающим равномерное
движение центра тяжести В. п. с групповой скоростью 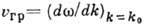 ,
и равенством
,
и равенством
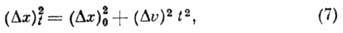
характеризующим расширение
со временем ("расплывание") В. п., где 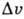 - среднеквадратичный разброс величины
- среднеквадратичный разброс величины 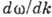
В квантовой механике для
волны, де Бройля частицы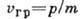 (где р, т - импульс и масса частицы), т. е. совпадает со ср. значением
классич. скорости частицы, а
(где р, т - импульс и масса частицы), т. е. совпадает со ср. значением
классич. скорости частицы, а 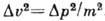 ,
где
,
где 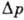 - среднеквадратичный
разброс по импульсам в В. п. Соотношения (6), (7) и (4) сыграли важную роль
в создании осн. квантовых представлений. Тот факт, что центр масс локализованного
в пространстве В. п., составленного из волн де Бройля, перемещается со скоростью
классич. частицы, явился иллюстрацией предельного перехода квантовомеханич.
законов движения к законам движения классич. частицы по классич. траектории.
Аналогично факт расплывания В. п. со временем способствовал принятию статистич.
интерпретации квантовой механики (поскольку из него следовало, что квадрат модуля
волновой функции нельзя рассматривать как плотность частицы). Учитывая,
что в квантовой теории
- среднеквадратичный
разброс по импульсам в В. п. Соотношения (6), (7) и (4) сыграли важную роль
в создании осн. квантовых представлений. Тот факт, что центр масс локализованного
в пространстве В. п., составленного из волн де Бройля, перемещается со скоростью
классич. частицы, явился иллюстрацией предельного перехода квантовомеханич.
законов движения к законам движения классич. частицы по классич. траектории.
Аналогично факт расплывания В. п. со временем способствовал принятию статистич.
интерпретации квантовой механики (поскольку из него следовало, что квадрат модуля
волновой функции нельзя рассматривать как плотность частицы). Учитывая,
что в квантовой теории 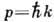 , из (3) непосредственно получается неопределенностей соотношение для
координаты и импульса:
, из (3) непосредственно получается неопределенностей соотношение для
координаты и импульса:
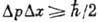
Для движения частицы во
внеш. поле в случае, когда спектр её энергии дискретен, также может быть рассмотрен
В. п., представляющий собой суперпозицию состояний с разл. значениями энергии.
Центр масс такого В. п. тоже движется по классяч. траектории, при этом для нек-рых
потенциалов поля (типа потенциала поля осциллятора) существуют нерасплывающиеся
волновые пакеты (см. Когерентное состояние).
При использовании соотношений
(6), (7) для распространения света в среде следует иметь в виду, что они получены
в предположении вещественности 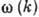 , т. е. в пренебрежении эффектами диссипации. Эти соотношения могут оказаться
неправильными при их формальном использовании в случае В. п. с частотами, лежащими
вблизи области т. н. аномальной дисперсии данной среды, где диссипац. эффектами
пренебрегать нельзя. В этой области частот понятие групповой скорости теряет
смысл, поскольку при движении В. п. будет
происходить его сильное экспоненциальное затухание, как это следует из выражения
(1).
, т. е. в пренебрежении эффектами диссипации. Эти соотношения могут оказаться
неправильными при их формальном использовании в случае В. п. с частотами, лежащими
вблизи области т. н. аномальной дисперсии данной среды, где диссипац. эффектами
пренебрегать нельзя. В этой области частот понятие групповой скорости теряет
смысл, поскольку при движении В. п. будет
происходить его сильное экспоненциальное затухание, как это следует из выражения
(1).

С. П. Аллилуев
Когда тот или иной физик использует понятие "физический вакуум", он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.
Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик Анри Пуанкаре, уже нельзя. Слишком много фактов противоречит этому.
Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование "моря" двух компенсирующих друг друга энергий в вакууме - положительной и отрицательной, а также "моря" компенсирующих друг друга частиц - виртуальных (то есть кажущихся) электронов и позитронов в вакууме.
Однако такая постановка является внутренне противоречивой (виртуальные частицы ненаблюдаемы и их по произволу можно считать в одном случае отсутствующими, а в другом - присутствующими) и противоречащей релятивизму (то есть отрицанию эфира, так как при наличии таких частиц в вакууме релятивизм уже просто невозможен). Подробнее читайте в FAQ по эфирной физике.
|
|