к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

РЕАЛЬНАЯ ФИЗИКА

Глоссарий по физике

А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

Спиновая температура

Спиновая температура - термодинамич. величина, характеризующая состояние внутр. квазиравновесия в подсистеме спиновых степеней свободы вещества. наиб. распространение понятие спиновой температуры получило при описании электронных и ядерных парамагнетиков . В этом случае спиновая температура T_S определяет вероятность W_i нахождения системы частиц, обладающих спином, в стационарном состоянии с энергией: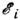

где Z - статистич. сумма. Соотношение (1) аналогично обычному каноническому распределению Гиббса, однако - лишь часть полной энергии системы, зависящая от спиновых переменных. Предполагается, что локальное внутр. равновесие в спиновой подсистеме (квазиравновесие) устанавливается гораздо быстрее, чем равновесие между спиновой подсистемой и остальными степенями свободы (истинное равновесие с температурой Т₀). Примером может служить система ядер, обладающих спином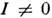 и гиромагн. отношением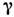, в твёрдом теле, помещённом во внеш. пост. магн. поле H. Взаимодействие магн. момента ядра с этим полем приводит к образованию 2I + 1 уровней энергии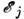, разделённых равными интервалами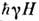 и соответствующих разл. значениям проекции I_z ядерного спина на направление Н (рис., а). Внутр. квазиравновесие в этой системе устанавливается благодаря спин-спиновым взаимодействиям между ядрами: 1) создаваемые ядерными магн. моментами локальные поля приводят к расфазировке прецессии спинов в поле Н за время поперечной релаксации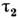, в результате сохраняющейся макроскопич. характеристикой системы остаётся ср. значение I_z; 2) взаимные «перевороты» ядерных спинов, вызванные спин-спиновым взаимодействием, приводят к «забыванию» их нач. распределения по состояниям также за время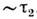. Поэтому на интервалах времени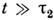 можно считать спиновую подсистему квазиравновесной. Обычно 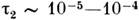с оказывается много меньше времени спин-решёточной релаксации 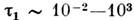с.

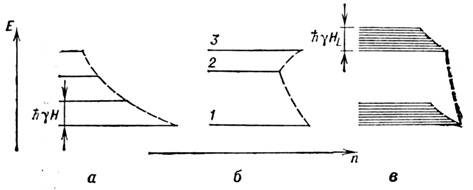
Энергетические диаграммы и квазиравновесные распределения населёнвостей парамагнитных спиновых систем в магнитном поле: а - I = 3/2, единая спиновая температура; б - различные спиновые температуры в неэквидистантном спектре; в - «зеемановская» и «спин-спиновая» спиновые температуры;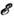 - энергия, и - населённость; пунктир соответствует распределению Больцмана.

Распределение (1) сводится при этом к Больцмана распределению населённостей n_i по уровням: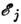

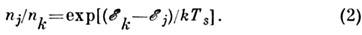
Если спиновая система не подвергается внеш. воздействиям, она приходит в равновесие с решёткой, играющей роль термостата; при этом T_S = T₀. Однако при воздействии резонансного радиочастотного магн. поля с частотой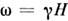 , индуцирующего квантовые переходы между соседними магн. уровнями [см. Ядерный магнитный резонанс (ЯМР)], населённости уровней постепенно выравниваются, что в соответствии с (2) означает повышение спиновой температуры. В пределе и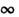 (насыщение ЯМР).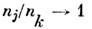

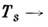
Понятие спиновой температуры обобщается также на системы с разл. расстояниями между соседними уровнями энергии, что типично для электронного парамагнитного резонанса, ядерного квадрупольного резонанса и др. В этом случае отсутствие резонанса между разл. переходами спектра препятствует установлению квазиравновесия с единой спиновой температурой T_S. Однако каждой паре уровней j, k можно приписать, следуя (2), свою «парциальную» спиновую температуру

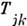
При насыщении к--л. перехода (напр., на рис., б) населённости этих уровней выравниваются и соответствующая спиновая температура 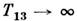, тогда как на др. переходах спиновая температура может оказаться как выше, так и ниже Т₀или стать отрицательной (см. Отрицательная температура ).Последнее означает, в соответствии с (2), что населённость верх. уровня больше, чем нижнего (см. уровни 3, 2 на рис., б). Возможность состояний с отрицательной спиновой температуры характерна для систем (не только спиновой природы), спектр энергии к-рых ограничен сверху. Такие состояния способны к вынужденному испусканию эл--магн. поля, с ними связана работа квантовых генераторов и усилителей (см. также Лазер).

Термодинамический смысл спиновой температуры более полно проявляется в твёрдых парамагнетиках при учёте энергии спин-спиновых взаимодействий. При этом каждый уровень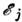 расщепляется в квазинепрерывную полосу шириной 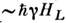, где H_L- ср. локальное поле. При 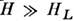квазиравновесие в такой системе описывается двумя спиновыми температурами: «зеемановской» T_sz и «спин-спиновой» T_SS. Они характеризуют соответственно распределения населённостей по уровням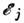и внутри непрерывных полос (рис., в).

Адиабатич. уменьшение поля Н за время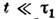 приводит к понижению спиновой температуры. В частности, при адиабаич. размагничивании до Н = 0 получается T_S = T₀H_L/H. Адиабатич. размагничивание электронных и ядерных парамагнетиков используют для магнитного охлаждения до температур ниже 1К.

В магнитоупорядоченных веществах (ферро- и антиферромагнетиках) аналогом спиновой температуры является эфф. температура подсистемы магнонов (см. Релаксация магнитная).

Литература по спиновой температуры

Гольдман М., Спиновая температура и ЯМР в твердых телах, пер. с англ., М., 1972;
Ацаркин В. А., Родак М. И., Температура спин-спиновых взаимодействий в электронном парамагнитном резонансе, «УФН», 1972, т. 107, с. 3;
Абрагам А., Гольдман М., Ядерный магнетизм: порядок и беспорядок, пер. с англ., т. 1-2, М., 1984.

В. А. Ацаркин

к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

Знаете ли Вы, что "гравитационное линзирование" якобы наблюдаемое вблизи далеких галактик (но не в масштабе звезд, где оно должно быть по формулам ОТО!), на самом деле является термическим линзированием, связанным с изменениями плотности эфира от нагрева мириадами звезд. Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМА

Рыцари теории эфира