Каноническое распределение Гиббса - распределение вероятностей состояний статистич. ансамбля систем, к-рые находятся в тепловом
равновесии со средой (термостатом) и могут обмениваться с ней энергией при пост.
объёме и пост. числе частиц; соответствует канонич. ансамблю Гиббса. К. р. Г.
установлено Дж. Гиббсом (J. Gibbs) в 1901. Равновесная
функция распределения f(р, q) зависит от координат и импульсов р, q всех частиц лить через Гамильтона функцию HN(p, q)
системы N частиц:
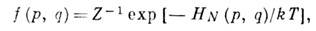
где Т - абс. темп-pa, Z - статистический интеграл ,определяемый из условия нормировки f и равный
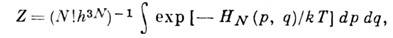
где интегрирование ведётся по фазовому пространству всех частиц, 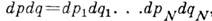 , h - постоянная Планка. Т. о., Z является функцией Т, N и объёма V.
К. р. Г. можно получить, если рассматривать совокупность данной системы и
термостата как одну замкнутую изолиров. систему и применить к ней микроканоническое распределение Гиббса
.Тогда малая подсистема, функцию распределения к-рой можно найти
интегрированием по фазовым переменным термостата, описывается К. р. Г.
(теорема Гиббса).
В квантовой статистике статистич. ансамбль характеризуется
распределенпем вероятностей wi квантовых состояний системы с энергией Ei-. К. р. Г. для квантовых систем имеет след. вид:
, h - постоянная Планка. Т. о., Z является функцией Т, N и объёма V.
К. р. Г. можно получить, если рассматривать совокупность данной системы и
термостата как одну замкнутую изолиров. систему и применить к ней микроканоническое распределение Гиббса
.Тогда малая подсистема, функцию распределения к-рой можно найти
интегрированием по фазовым переменным термостата, описывается К. р. Г.
(теорема Гиббса).
В квантовой статистике статистич. ансамбль характеризуется
распределенпем вероятностей wi квантовых состояний системы с энергией Ei-. К. р. Г. для квантовых систем имеет след. вид:
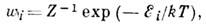
где Z - статистич. сумма, определяемая из условия нормировки (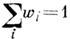 ) и равная
) и равная 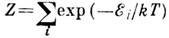 , суммирование ведётся по всем квантовым состояниям допустимой симметрии.
К. р. Г. в квантовом случае можно представить с помощью статистического оператора (матрицы плотности)
, суммирование ведётся по всем квантовым состояниям допустимой симметрии.
К. р. Г. в квантовом случае можно представить с помощью статистического оператора (матрицы плотности) 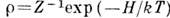 , где H - гамильтониан
системы. Такая форма К. р. Г. удобна для приложений, особенно с
использованием представления вторичного квантования для гамильтониана.
К. р. Г. как в классич., так и в квантовом случае позволяет вычислить
свободную энергию (Гельмгольца энергию)в переменных Т, V, N, равную F=-kTlnZ, где Z
- статистич. интеграл или статистич. сумма. К. р. Г. соответствует
максимуму информац. энтропии при заданной средней энергии и при
сохранении нормировки.
, где H - гамильтониан
системы. Такая форма К. р. Г. удобна для приложений, особенно с
использованием представления вторичного квантования для гамильтониана.
К. р. Г. как в классич., так и в квантовом случае позволяет вычислить
свободную энергию (Гельмгольца энергию)в переменных Т, V, N, равную F=-kTlnZ, где Z
- статистич. интеграл или статистич. сумма. К. р. Г. соответствует
максимуму информац. энтропии при заданной средней энергии и при
сохранении нормировки.
Знаете ли Вы, что, как и всякая идолопоклонническая религия, релятивизм ложен в своей основе. Он противоречит фактам. Среди них такие:
1. Электромагнитная волна (в религиозной терминологии релятивизма - "свет") имеет строго постоянную скорость 300 тыс.км/с, абсурдно не отсчитываемую ни от чего. Реально ЭМ-волны имеют разную скорость в веществе (например, ~200 тыс км/с в стекле и ~3 млн. км/с в поверхностных слоях металлов, разную скорость в эфире (см. статью "Температура эфира и красные смещения"), разную скорость для разных частот (см. статью "О скорости ЭМ-волн")
2. В релятивизме "свет" есть мифическое явление само по себе, а не физическая волна, являющаяся волнением определенной физической среды. Релятивистский "свет" - это волнение ничего в ничем. У него нет среды-носителя колебаний.
3. В релятивизме возможны манипуляции со временем (замедление), поэтому там нарушаются основополагающие для любой науки принцип причинности и принцип строгой логичности. В релятивизме при скорости света время останавливается (поэтому в нем абсурдно говорить о частоте фотона). В релятивизме возможны такие насилия над разумом, как утверждение о взаимном превышении возраста близнецов, движущихся с субсветовой скоростью, и прочие издевательства над логикой, присущие любой религии.
4. В гравитационном релятивизме (ОТО) вопреки наблюдаемым фактам утверждается об угловом отклонении ЭМ-волн в пустом пространстве под действием гравитации. Однако астрономам известно, что свет от затменных двойных звезд не подвержен такому отклонению, а те "подтверждающие теорию Эйнштейна факты", которые якобы наблюдались А. Эддингтоном в 1919 году в отношении Солнца, являются фальсификацией. Подробнее читайте в FAQ по эфирной физике.
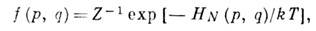
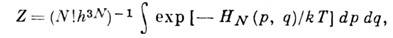
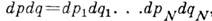 , h - постоянная Планка. Т. о., Z является функцией Т, N и объёма V.
К. р. Г. можно получить, если рассматривать совокупность данной системы и
термостата как одну замкнутую изолиров. систему и применить к ней микроканоническое распределение Гиббса
.Тогда малая подсистема, функцию распределения к-рой можно найти
интегрированием по фазовым переменным термостата, описывается К. р. Г.
(теорема Гиббса).
В квантовой статистике статистич. ансамбль характеризуется
распределенпем вероятностей wi квантовых состояний системы с энергией Ei-. К. р. Г. для квантовых систем имеет след. вид:
, h - постоянная Планка. Т. о., Z является функцией Т, N и объёма V.
К. р. Г. можно получить, если рассматривать совокупность данной системы и
термостата как одну замкнутую изолиров. систему и применить к ней микроканоническое распределение Гиббса
.Тогда малая подсистема, функцию распределения к-рой можно найти
интегрированием по фазовым переменным термостата, описывается К. р. Г.
(теорема Гиббса).
В квантовой статистике статистич. ансамбль характеризуется
распределенпем вероятностей wi квантовых состояний системы с энергией Ei-. К. р. Г. для квантовых систем имеет след. вид:
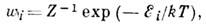
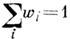 ) и равная
) и равная 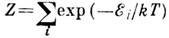 , суммирование ведётся по всем квантовым состояниям допустимой симметрии.
К. р. Г. в квантовом случае можно представить с помощью статистического оператора (матрицы плотности)
, суммирование ведётся по всем квантовым состояниям допустимой симметрии.
К. р. Г. в квантовом случае можно представить с помощью статистического оператора (матрицы плотности) 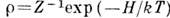 , где H - гамильтониан
системы. Такая форма К. р. Г. удобна для приложений, особенно с
использованием представления вторичного квантования для гамильтониана.
К. р. Г. как в классич., так и в квантовом случае позволяет вычислить
свободную энергию (Гельмгольца энергию)в переменных Т, V, N, равную F=-kTlnZ, где Z
- статистич. интеграл или статистич. сумма. К. р. Г. соответствует
максимуму информац. энтропии при заданной средней энергии и при
сохранении нормировки.
, где H - гамильтониан
системы. Такая форма К. р. Г. удобна для приложений, особенно с
использованием представления вторичного квантования для гамильтониана.
К. р. Г. как в классич., так и в квантовом случае позволяет вычислить
свободную энергию (Гельмгольца энергию)в переменных Т, V, N, равную F=-kTlnZ, где Z
- статистич. интеграл или статистич. сумма. К. р. Г. соответствует
максимуму информац. энтропии при заданной средней энергии и при
сохранении нормировки.
