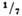 от
расстояния между объёмными рефлексами, указывают на поверхностную периодичность,
в 7 раз большую соответствующего периода в объёме.
от
расстояния между объёмными рефлексами, указывают на поверхностную периодичность,
в 7 раз большую соответствующего периода в объёме.Реконструкция поверхности - образование на чистых поверхностях монокристаллов структур, элементарная ячейка к-рых имеет
период, отличающийся от периода в объёме кристалла (в параллельных поверхности
плоскостях) и обычно превышающий его в неск. раз. Развитие техники сверхвысокого
вакуума (давление p ! 10-7 Па) позволило наблюдать атомарно-чистую,
свободную от примесей поверхность, полученную сколом и сохраняющуюся неизменной
в течение неск. ч.
Рис. 1. Схема электронограммы от поверхности
кремния (111). Интенсивные пятна - рефлексы от объёма кристалла; слабые рефлексы,
расположенные на расстоянии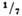 от
расстояния между объёмными рефлексами, указывают на поверхностную периодичность,
в 7 раз большую соответствующего периода в объёме.
от
расстояния между объёмными рефлексами, указывают на поверхностную периодичность,
в 7 раз большую соответствующего периода в объёме.

Большинство исследований выполняется методом
дифракции медленных электронов (ДМЭ)[1] или фотоэмиссионными методами [2]. В
методе ДМЭ электроны с энергиями 1 -10 эВ
имеют большие сечения рассеяния и глубина их проникновения в кристалл составляет
5-10 A, т. е. 2-3 монослоя атомов. Схема электронограммы ДМЭ для чистой
поверхности кремния (111) приведена на рис. 1. Она свидетельствует о появлении
поверхностного периода, в 7 раз превышающего период кристаллич. решётки в объёме.
На поверхности образуется сетка размерами (7 x 7). В общем случае говорят об
образовании сетки (n x m)q, где n и т - коэф.
пропорциональности между поверхностными и объёмными векторами трансляций, q
- угол между поверхностными векторами трансляций. Р. п. наблюдалась также на
поверхностях Ge, GaAs, GaSb, InSb, CdS, CdTe, Те и др. полупроводниковых
материалов.
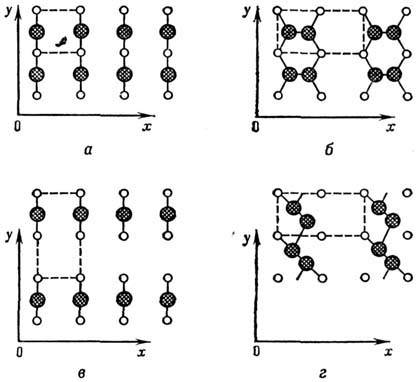
Рис. 2. Поверхностные элементарные ячейки для
3 моделей замыкания оборванных связей на поверхности (100) Si: а - нереконструированная
поверхность; каждый атом верхнего слоя (большие кружки) связан 2 гибридизированными
связями с атомами 2-го слоя (маленькие кружки) и имеет две оборванные свободные
связи; элементарная ячейка показана пунктиром; б - модель двойных связей
(удвоение поверхностной элементарной ячейки по оси 0х); в - модель
с поверхностными вакансиями; на поверхности отсутствуют ряды атомов, оставшиеся
образуют сдвоенные связи с атомами 2-го слоя; элементарная ячейка удвоена по
Оу; г - модель цепочек; каждый поверхностный атом имеет 2 одиночные связи
с соседями в цепочке, ещё одну связь с атомами 2-го слоя, а оставшаяся 4-я связь
даёт вклад в молекулярную орбиталь, охватывающую всю цепочку.
Теоретич. рассмотрение Р. п. основано на кванто-во-хим.
расчётах. На свободной поверхности гомео-полярных кристаллов при сколе образуются
оборванные ненасыщенные ковалентные связи. Установление новой равновесной конфигурации
поверхностных атомов происходит путём таких их перемещений, к-рые приводят к
замыканию оборванных связей и т. о. к понижению энергии системы. При вычислениях
полной энергии кристалла размеры поверхностной элементарной ячейки берутся из
эксперимента, а характер замыкания связей выбирается модельным способом. На
рис. 2 рядом с идеальной нереконструированной поверхностью
(100) приведены 3 модели разл. замыкания оборванных связей. Сравнение с экспериментом
не позволяет отдать предпочтение к--л. из этих моделей, т. к. расположение дифракц.
рефлексов отражает только тран-сляц. симметрию поверхности. Информация о взаимном
расположении атомов в элементарной ячейке содержится в распределении интенсивности
в дифракц. рефлексах. Анализ этого распределения является сложной матем. задачей.
Эксперимент показывает, что симметрия поверхности
меняется при изменении температуры [3], т. е. на поверхности происходят структурные
фазовые превращения. Если такое превращение идёт по типу фазового перехода
2-го рода, то можно исследовать устойчивость идеальной поверхности относительно
разл. смещений поверхностных атомов из положений равновесия. Любое смещение
поверхностного атома можно представить в виде суперпозиции смещений, соответствующих
нормальным колебаниям (см. Колебания кристаллической решётки ).Смещение
x поверхностного атома из положения равновесия x0 характеризуется
волновым вектором  параллельным поверхности. Если смещение поверхностного атома приводит к увеличению
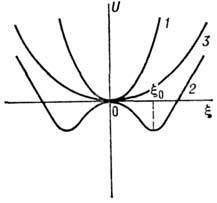
потенц. энергии U (кривая 1, рис. 3), то исходному состоянию
поверхности соответствует минимум U и поверхность
устойчива. Если смещение поверхностных атомов приводит к уменьшению потенц.
энергии (кривая 2 вблизи начала координат), то исходное состояние соответствует
максимуму потенц. энергии. Поверхность при этом неустойчива, происходит Р. п.
Новые положения равновесия x0 определяются ангармонизмом колебаний.
С учётом ангармонич. членов U(x) имеет вид полной кривой 3.
параллельным поверхности. Если смещение поверхностного атома приводит к увеличению
потенц. энергии U (кривая 1, рис. 3), то исходному состоянию
поверхности соответствует минимум U и поверхность
устойчива. Если смещение поверхностных атомов приводит к уменьшению потенц.
энергии (кривая 2 вблизи начала координат), то исходное состояние соответствует
максимуму потенц. энергии. Поверхность при этом неустойчива, происходит Р. п.
Новые положения равновесия x0 определяются ангармонизмом колебаний.
С учётом ангармонич. членов U(x) имеет вид полной кривой 3.
Рис. 3. Зависимость потенциальной энергии U от величины смещения поверхностного атома x: кривая (1)соответствует
устойчивому равновесию; кривая (г) изображена с учётом ангармонизма колебаний
и соответствует реконструированной поверхности; x0 - новые положения
равновесия.
Условие максимума или минимума потенц. энергии
определяется знаком производной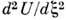 ,
к-рая пропорц. квадрату частоты поверхностного
колебания w2( ). Значение , для к-рого
w(
,
к-рая пропорц. квадрату частоты поверхностного
колебания w2( ). Значение , для к-рого
w( 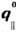 ) =
0 (мягкая мода),
) =
0 (мягкая мода), 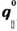 соответствует
соответствует 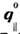 колебанию, по отношению к к-рому поверхность неустойчива. Именно
колебанию, по отношению к к-рому поверхность неустойчива. Именно 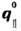 определяет пространственный период новой устойчивой поверхностной конфигурации
атомов, соответствующей реконструированной поверхности.
определяет пространственный период новой устойчивой поверхностной конфигурации
атомов, соответствующей реконструированной поверхности.
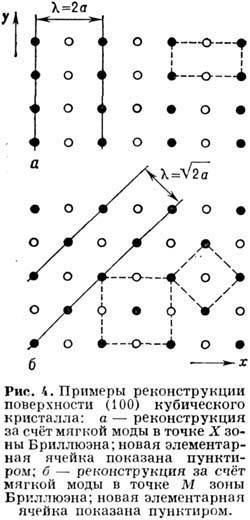
На рис. 4. приведены 2 примера Р. п. (100) кубич.
кристалла. Если мягкая мода возникает в точке X зоны
Бриллюэна (см. Бриллюэна зона)с координатами (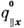 =
p/a,
=
p/a,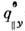 = 0), то на поверхности устанавливается "волна" статич. смещений
с периодом, где а -
= 0), то на поверхности устанавливается "волна" статич. смещений
с периодом, где а -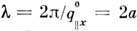 период
нереконструированной поверхности. Возникают чередующиеся ряды поднявшихся вверх
и опустившихся вниз атомов. Происходит удвоение периода решётки вдоль оси х. Если мягкая мода возникает в точке М зоны Бриллюэна с координатами
период
нереконструированной поверхности. Возникают чередующиеся ряды поднявшихся вверх
и опустившихся вниз атомов. Происходит удвоение периода решётки вдоль оси х. Если мягкая мода возникает в точке М зоны Бриллюэна с координатами
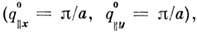
то на поверхности устанавливается волна статических смещений в направлении, составляющем угол 45° с осями 0х и 0у и с периодом
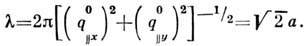
Такую структуру обозначают (2 x 2) R 45° или С(2 x x 2).
Возможные перестройки поверхности, происходящие
по типу фазового перехода 2-го рода, можно найти теоретико-групповыми методами.
Р. п. охватывает неск. приповерхностных кристаллич. плоскостей, составляющих
приповерхностный слой [4].
Р. п. с большим периодом, напр. структуры (7
x 7) на поверхности (111) Si, связывают с возникновением узкой энергетич.
зоны поверхностных состояний для электронов оборванных связей. На поверхности
(111) Si на каждый поверхностный атом приходится 1 оборванная связь. Поэтому
зона поверхностных состояний заполнена только наполовину. Энергию электрона
в такой зоне можно рассчитывать методом сильной связи (см. Зонная теория):
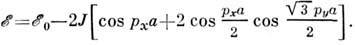
Здесь рх и ру - проекции квазиимпульса электрона, J - интеграл перекрытия электронных
волновых функций. Ферми-поверхность для таких электронов является шестиугольником.
Из-за наличия плоских граней электрон-фононное взаимодействие даёт аномально
большой сдвиг частоты нормального колебания с волновым вектором q||=
2рF (рF - импульс Ферми). Если при нек-ром сдвиге
частоты результирующая частота w2(2рF) = 0,
то поверхность кристалла неустойчива относительно такого колебания и произойдёт
Р. п. Устойчивое состояние соответствует волне статич. смещений с длиной волны
l = 2p/q||= p/рF, соизмеримой
с постоянной решётки ml = па, где т и n - целые
числа. Период новой структуры определяется числом п. Для поверхности
(111) Si число n = 7, что соответствует структуре (7x7).
Исследования атомарно-чистой поверхности важны для понимания свойств границы раздела кристаллов. По-видимому, нач. стадии адсорбции и роста кристаллов (см. Кристаллизация)определяются свойствами реконструированных границ раздела [5].

|
|