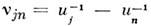Глоссарий по физике

Нестационарные нелинейные оптические явления

Нестационарные нелинейные оптические явления - нелинейные оптич. явления, наблюдаемые в импульсных и в модулированных во времени полях эл--магн. волн. Большинство Н. н. о. я. обусловлено инерционностью среды, как инерционностью локального нелинейного отклика, так и инерционностью отклика среды в целом. Инерционность среды проявляется в том, что её линейная и (или) нелинейная поляризация в заданной точке в данный момент времени зависит от значения исходных полей в более ранние моменты времени. Инерционность нелинейного отклика среды сказывается, если время отклика нелинейности больше длительности оптич. импульса или характерного времени модуляции волны. Инерционность линейного отклика проявляется как частотная (временная) дисперсия линейного показателя преломления среды. При нелинейном взаимодействии она чаще всего выступает в виде расстройки 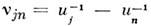групповых скоростей u_j и и_п взаимодействующих волн (см. Групповой синхронизм).

Аналитически Н. н. о. я. описываются одним нелинейным ур-нием или системой связанных ур-ний в частных производных и соответствуют самовоздействию или взаимодействию световых волн (см. Нелинейная оптика). К Н. н. о. я. относятся самомодуляция импульса

(сжатие и расширение), самофокусировка ,процессы преобразования оптич. частот при параметрич. взаимодействии и вынужденном рассеянии света. Напр., самомодуляция светового импульса описывается укороченным ур-нием вида

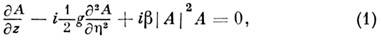
где А - комплексная амплитуда волны, h = t - z/u, t - текущее время, и - групповая скорость, параметр g = - u^-2du/dw характеризует дисперсию групповой скорости. Величина b пропорциональна нелинейному преломления показателю среды n₂, причём ур-ние (1) соответствует безынерционному нелинейному отклику среды. С b0 связано возникновение фазовой самомодуляции импульса, приводящей к уширению его спектра, ширина которого пропорциональна макс. интенсивности импульса, нелинейности показателя преломления п₂ и пройденному расстоянию. Вследствие дисперсии среды разные спектральные компоненты импульса распространяются с разл. скоростью. В фокусирующей среде (b > 0) эффект фазовой самомодуляции и аномальная дисперсия групповой скорости (g < 0) приводят к сжатию импульса. Это происходит из-за того, что низшие частоты, возникающие на хвосте импульса, догоняют высокие частоты, появляющиеся на его фронте. В нелинейной среде с нормальной дисперсией групповой скорости (g > 0) импульс, напротив, расплывается быстрее, чем в линейной среде. Эффекты сжатия и расплывания импульса проявляются, напр., при распространении мощных нико- и фемтосекундных лазерных импульсов в оптич. волокнах. Особый практич. интерес представляет режим самосжатия, в к-ром форма импульса в среде остаётся неизменной - образуется т. н. соли-тон оптический.

Процессы самосжатия и саморасширения импульсов во многом аналогичны процессам самофокусировки и самодефокусировки световых пучков в стационарном случае. Последние наблюдают, если время отклика нелинейности t_нл меньше длительности импульса. При нестационарном самовоздействии световых импульсов нелинейная добавка dn к показателю преломления (нелинейный отклик) среды определяется соотношением

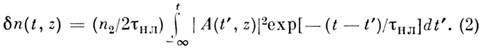
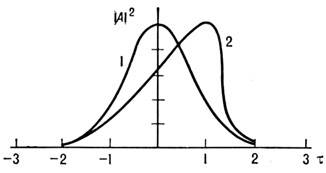
В силу (2) нарастание dn(t,z)во времени происходит быстрее, нежели спад; это приводит к асимметричному уширению спектра: смещение частоты импульса происходит в основном в область НЧ (рис. 1).

Рис. 1. Вид уширенного спектра гауссовского импульса длительностью 2,7 пс в среде с временем релаксации нелинейности 9 пс; l₀ - длина волны исходного импульса.

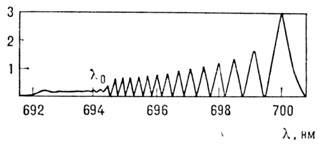
В случае нестационарной самофокусировки сверхкоротких световых импульсов (рис. 2, а)на переднем фронте импульса нелинейный отклик среды ещё не успевает установиться, поэтому эта часть импульса распространяется как в линейной среде, испытывая лишь дифракцию (лучи а и б рис. 2, б). При возникновении значит. добавки dn на центр. и задней частях импульса световой пучок самофокусируется (лучи в, г и т. д. рис. 2, б). В результате световой пучок сверхкороткой длительности принимает форму рупора, как показано на рис. 2 (б). Для нелинейности, возникающей под действием элект-рич. поля, подобная картина самофокусировки наблюдается при длительностях импульсов ~ 10^-11-10^-12с.

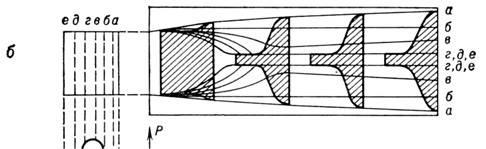
Рис. 2. Картина нестационарной самофокусировки светового импульса: а - форма импульса; б - форма пучка.

При самовоздействии достаточно мощных световых импульсов искажение формы импульса возможно и в безынерционной среде. Важную роль при этом играет зависимость групповой скорости от интенсивности I распространяющегося импульса и ~ (п₀ + n₂I)^-1. Середина гауссовского импульса (рис. 3), имеющая большую интенсивность, чем передний фронт, имеет меньшую групповую скорость и отстаёт (при п₂ > 0), что приводит к укручению хвоста импульса. Накапливающиеся с расстоянием изменения формы импульса могут быть столь сильными, что возможно образование ударной волны огибающей (рис. 3). Это происходит на расстоянии L_yд = 7сt_имп/dn_макс, где dn_макс - макс. изменение показателя преломления.

Рис. 3. Изменение формы гауссовского импульса (1) в безынерционной нелинейной среде (2) при z=L_уд, t=t/t_имп.

Широкий класс Н. н. о. я. связан с преобразованием оптич. частот и процессами вынужденного рассеяния света. При взаимодействии световых волн нестационарность явлений связана гл. обр. с расстройкой групповых скоростей. Первоначально синхронизов. импульсы разных частот распространяются в среде с разными групповыми скоростями, что приводит к их разбеганию и прекращению взаимодействия. Этот эффект начинает сказываться, когда время группового запаздывания импульсов t_зап = z/u_j - z/u_n становится сравнимым с их длительностью (t_имп 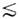t_зап). При генерации оптич. гармоник групповая расстройка ограничивает спектральную ширину фазового синхронизма:

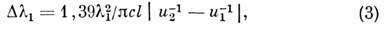
где l₁ - длина волны осн. излучения, с - скорость света в вакууме, l - длина нелинейного взаимодействия, и₁ и u₂ - групповые скорости осн. волны и волны гармоники. Если ширина спектра осн. импульса превышает (3), то происходит удлинение импульса высшей гармоники и ограничение её макс. амплитуды. Иначе говоря, нестационарный процесс умножения оптич. частот оказывается менее эффективным, чем стационарный. В кристалле LiNbO₃ длиной 1 см нестационарность нелинейного процесса сказывается при длительности осн. импульса 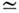6 пс. 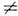Для импульсов субпикосекундной длительности наряду с расстройкой групповых скоростей определённую роль в нелинейном процессе может играть дисперсионное расплывание взаимодействующих импульсов, связанное с дисперсией групповой скорости (g 0).

Нестационарные режимы невырожденного трёхча-стотного и четырёхчастотного взаимодействия световых волн отличаются большим разнообразием. Общим, однако, является то, что смещение импульсов друг относительно друга из-за различия групповых скоростей приводит к снижению эффективности взаимодействия, к наличию предельного сужения усиливаемых или генерируемых импульсов. Особо стоит сказать о возможности модового режима параметрич. усиления в диспергирующей нелинейной среде, когда групповая скорость волны накачки является промежуточной по отношению к групповым скоростям сигнальной и холостой волн (см. Параметрическое рассеяние ).При этом форма усиливаемого импульса сохраняется, а его амплитуда экспоненциально нарастает с расстоянием.

Среди нестационарных процессов вынужденного рассеяния света особое место занимает комбинац. рассеяние (КР), к-рое широко используется для измерения спектроскопич. параметров среды. При КР падающее излучение частоты w_н преобразуется в излучение сток-совой частоты w_с за счёт возбуждения колебаний среды на частоте W: (w_н = w_c+W). Нестационарное вынужденное КР может быть обусловлено как инерционностью, напр. молекулярных колебаний (конечными временами затухания колебат. энергии Т₁ и дефазиров-ки Т₂, см. Двухуровневая система), так и расстройкой групповых скоростей волн накачки и_н и стоксовой волны и_с. Эффекты, связанные с T₂ (в конденсир. средах Т₂ 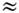10^-11 - 10^-12 с), могут наблюдаться "в чистом виде", когда изменением населённости уровней под действием процесса можно пренебречь. В существенно нестационарном режиме рассеяния (длительность импульса накачки t_н << Т₂)при v_HC = 0 возбуждаемый стоксов импульс может быть значительно задержан, а его длительность гораздо меньше t_н (рис. 4). Картину вынужденного КР существенно изменяет и наличие групповой расстройки (v_HC 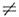0).

Рис. 4. Схема поведения стоксовой волны |А_С| и молекулярных колебаний | Q| в различных сечениях комбинационно-активной среды для прямоугольного импульса накачки |А_Н|.

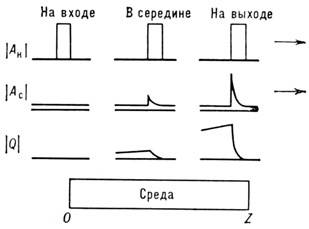
В случае попутного взаимодействия волн накачки и стоксовой наиб. влияние на процесс оказывает фазовая модуляция накачки. На расстояниях, превышающих длину группового запаздывания L_rp = p/|v_HC|Dw_H (Dw_H - ширина спектра накачки), происходит рассогласование фаз накачки и стоксовой волны, к-рое приводит к уменьшению эфф. длины взаимодействия и в нек-рых случаях к полному подавлению вынужденного КР. Волновая нестационарность особенно ярко проявляется при встречном взаимодействии волн накачки и стоксовой, где 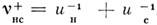. В этом режиме передний фронт стоксова импульса всё время взаимодействует с неистощённой накачкой, вследствие чего интенсивность стоксовой волны может значительно превышать интенсивность накачки. При одноврем. проявлении волновой и связанной с T₂ локальной нестационарности возможно возникновение режима экспоненциального нарастания стоксовых импульсов в среде с нормальной дисперсией (u_с > и_н)при z > t_H/|v_HC|.

Нестационарные эффекты, проявляющиеся при вынужденном КР, могут встречаться также и в процессе вынужденного рассеяния Мандельштама-Бриллюэна и др.

Определённый круг Н. н. о. я. связан с т. н. когерентным распространением световых импульсов в резонансных средах (см. Самоиндуцированная прозрачность, Фотонное эхо).

Литература по нестационарным нелинейным оптическим явлениям

1. Ахманов С. А., Сухоруков А. П., Хохлов Р. В., Самофокусировка и дифракция света в нелинейной среде, "УФН", 1967, т. 93, с. 19;
2. Ахманов С. А., Чир-кин А. С., Статистические явления в нелинейной оптике, М., 1971;
3. Ахманов С. А., Коротеев Н. И., Методы нелинейной оптики в спектроскопии рассеяния света, М., 1981;
4. Остон Д., Пикосекундная нелинейная оптика, в кн.: Сверхкороткие световые импульсы, пер. с англ., М., 1981;
5. Ахманов С. А., Выслоух В. А., Чиркин А. С. Самовоздействие волновых пакетов в нелинейной среде и генерация фемтосекундных лазерных импульсов, "УФН", 1986, т. 149, с. 449;
6. Ахманов С. А., Выслоух В. А., Чиркин А. С. Оптика фемтосекундных лазерных импульсов, М., 1988.

А. С. Чиркин

к библиотеке   к оглавлению   FAQ по эфирной физике   ТОЭЭ   ТЭЦ   ТПОИ   ТИ  

Знаете ли Вы, что только в 1990-х доплеровские измерения радиотелескопами показали скорость Маринова для CMB (космического микроволнового излучения), которую он открыл в 1974. Естественно, о Маринове никто не хотел вспоминать. Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМА Рыцари теории эфира

10.11.2021 - 12:37: ПЕРСОНАЛИИ - Personalias -> WHO IS WHO - КТО ЕСТЬ КТО - Карим_Хайдаров. 10.11.2021 - 12:36: СОВЕСТЬ - Conscience -> РАСЧЕЛОВЕЧИВАНИЕ ЧЕЛОВЕКА. КОМУ ЭТО НАДО? - Карим_Хайдаров. 10.11.2021 - 12:36: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от д.м.н. Александра Алексеевича Редько - Карим_Хайдаров. 10.11.2021 - 12:35: ЭКОЛОГИЯ - Ecology -> Биологическая безопасность населения - Карим_Хайдаров. 10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> Проблема государственного терроризма - Карим_Хайдаров. 10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> ПРАВОСУДИЯ.НЕТ - Карим_Хайдаров. 10.11.2021 - 12:34: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вадима Глогера, США - Карим_Хайдаров. 10.11.2021 - 09:18: НОВЫЕ ТЕХНОЛОГИИ - New Technologies -> Волновая генетика Петра Гаряева, 5G-контроль и управление - Карим_Хайдаров. 10.11.2021 - 09:18: ЭКОЛОГИЯ - Ecology -> ЭКОЛОГИЯ ДЛЯ ВСЕХ - Карим_Хайдаров. 10.11.2021 - 09:16: ЭКОЛОГИЯ - Ecology -> ПРОБЛЕМЫ МЕДИЦИНЫ - Карим_Хайдаров. 10.11.2021 - 09:15: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Екатерины Коваленко - Карим_Хайдаров. 10.11.2021 - 09:13: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вильгельма Варкентина - Карим_Хайдаров.