Метод молекулярной динамики. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Молекулярной динамики метод - собирательное название неск. численных методов решения разл. физ. задач при помощи моделирования (имитации) движения атомов, молекул, коллоидных и т. п. частиц, составляющих исследуемую систему. Обычно предполагают известными законы взаимодействия между частицами в рамках классич. механики. Численно интегрируя ур-ния механики, можно проследить за движением частиц и, усредняя по времени и по всем частицам, попытаться вывести микро- и макроскопич. характеристики изучаемой системы. При этом обычно исходят из предположения (поддающегося проверке при помощи M. д. м.), что рассматриваемая система является эргодической (см. Эргодичность ).Реальные модели могут содержать не более неск. млн. частиц; но даже системы, состоящие из неск. десятков или сотен атомов или молекул, представляют интерес. Для описания макроскопич. тел или сред применяют ряд спец. приёмов и методов. M. д. м. особенно полезен при исследовании таких систем (жидкость, плотная плазма и т. д.), в к-рых ср. кинетич. энергия К сравнима с потенц. энергией U. При этом отсутствует малый параметр, позволяющий развить, напр., теорию твёрдых тел (K/U << 1) и газов (U/K << 1). В зависимости от размеров системы и времени наблюдения за её эволюцией, а также с точки зрения изучаемых вопросов (стационарные состояния и термодинамика, неравновесные процессы и физ. кинетика и т. п.) все разновидности M. д. м. представляют собой иерархич. структуру - от численных экспериментов динамич. типа до динамич. Монте-Карло метода .В отличие от метода Монте-Карло, разработанного для вычисления равновесных величин, M. д. м. позволяет описать приближение системы к состоянию равновесия. Впервые метод молекулярной динамики был использован в работах Б. Олдера (В. Alder) и T. Вайнрайта (Th. Wainwright) в 1957, а также А. Рах-мана (A. Rahman) в 1964.

Численное моделирование в методе молекулярной динамики

С помощью адекватного метода вычислит. математики численно интегрируют ур-ния движения классич. механики для всех частиц системы при заданных потенциалах межчастичных взаимодействий, внеш. полях, связях, начальных и граничных условиях. В простейшем случае одноатомной ван-дер-ваальсовой жидкости решают след. ур-ния:

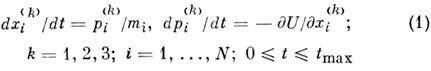
(х_i^(k) и p_i^(k) - k-я координата и импульс i-й молекулы, а

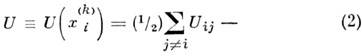
потенц. энергия системы N молекул, U_ij - потенциал взаимодействия i-й и j-и молекул, зависящий только от расстояния между ними, m_i - масса i-й молекулы, t - время) с нач. условиями

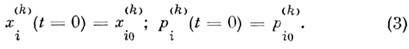
Если рассматриваемая система N частиц является частью макроскопич. изотропной системы, то обычно используют периодич. граничные условия, т. е. рассматривают N частиц в ограниченном объёме, к-рый, периодически повторяясь, заполняет всё пространство. При N>= 3 и обычно используемых межмолекулярных потенциалах аналитич. решение задачи (1) - (3) невозможно, поэтому вычисляют дискретное отображение фазовой траектории системы через нек-рые, обычно равные промежутки времени Dt (шаг по времени) с помощью численной схемы, связывающей значения координат и импульсов молекул в разл. последовательные моменты времени. Численная схема строится так, чтобы при Dt -> 0 вычисленные отображения сходились к точным решениям.

Чтобы проследить за движением молекул на промежутке времени 0 <=t <= t_max, следует задать нач. положения и импульсы частиц (3). По смыслу задачи они обычно не заданы, и их следует выбирать так, чтобы ответ существенно не зависел от привнесённого ими произвола, а средние по времени устанавливались с ростом t_maxпо возможности быстрее. T. о., вариации нач. данных и t_max - обязательный элемент метода молекулярной динамики. Однако никаких строгих правил их выбора нет. В задаче подобного типа обычно оказывается достаточной нач. расстановка частиц в виде правильной решётки, т. к. уже через неск. сотен шагов Dt этот порядок полностью исчезает. Если же нач. скорости взять излишне упорядоченными, то могут возникнуть процессы (типа столкновения пучков), сильно затягивающие переход к термодинамич, равновесию, что требует больших t_max. Поэтому нач. скорости задают случайным образом.

Выбор величины шага Dt основан на неск. соображениях: необходимо, чтобы Dt был на неск. порядков меньше периода колебаний атомов t₀. Более точно Dt подбирают в зависимости от используемой числ. схемы, типа ЭВМ, конкретного вида межмолекулярного потенциала, полной энергии и требуемой точности вычисляемых средних.

Обычно изучают замкнутые системы, в к-рых полная энергия сохраняется, а температуру T определяют по ср. кинетич. энергии системы:

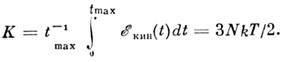
Даже для небольших N и "хороших" начальных условий величина К существует и устанавливается со скоростью ~ t_max^1/2 характерной для эргодич. систем. Распределение по импульсам оказывается биномиальным (из-за ограниченности полной энергии), т. е. лишь при N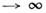

стремится к максвелловскому. Всё это служит основанием для применения понятия температуры к системе, подчиняющейся микроканонич. распределению. Введение к--л. метрики в фазовом пространстве позволяет определить и энтропию такой системы. Вычисление давления основано на применении вириала теоремы, требует эргодичности системы и предполагает близость средних по микроканонич. ансамблю к средним по канонич. ансамблю Гиббса, что имеет место при N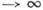

Такого рода поведение динамических систем наз. сто-хастичностью. Осн. механизм, вызывающий появление стохастичности,- неустойчивость движения, приводящая к расходимости (обычно экспоненциальной) близких фазовых траекторий и явлению перемешивания, к-рое приводит к эргодичности. В методе молекулярной динамики, к-рый применяют для исследования конденсир. систем, всегда имеют дело с неустойчивостью и стохастичностью. С одной стороны, это оправдывает применение метода молекулярной динамики для термодинамич. исследований, а с другой - означает, что точное вычисление траекторий, по-видимому, в принципе невозможно. Однако возможно приближённое вычисление дискретных отображений этих траекторий с наперёд заданной точностью при заданных t_max.

При разработке конкретного метода молекулярной динамики необходимо обратить внимание на то, как алгоритм передаёт нек-рые важные свойства имитируемой динамич. системы, напр. сохранение интегралов движения. Полная энергия консервативной динамич. системы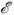

_полндолжна сохраняться. Легко построить M. д. м., в к-рых

_полнсохраняется автоматически. Однако обычные алгоритмы интегрирования дифференц. ур-ний приводят к зависимости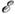

_полн(t, Dt), к-рая служит для грубого контроля за правильностью вычислений. Несохранение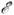

_полнсвидетельствует либо об ошибке в выборе Dt, либо о непригодности численной схемы. В нестационарных задачах метода молекулярной динамики этот критерий вообще бесполезен. Если в рассматриваемой системе интегралом движения является импульс, то метод молекулярной динамики обычно автоматически сохраняет эту величину, т. к. при вычислении межмолекулярных сил явно используется третий закон Ньютона.

Другое важное свойство траекторий динамических систем - обратимость во времени - также может быть выполнено автоматически в методе молекулярной динамики. T. о., легко убедиться, что в методе молекулярной динамики проблемы стохастичности динамич. систем и обратимости уравнений механики во времени никак не связаны между собой. Описанный метод замкнут, ибо его основания и результаты можно проверить внутр. образом, в рамках самого этого подхода.

Другие методы молекулярной динамики

Объект исследования метода молекулярной динамики - движение всех частиц системы. Во мн. случаях интерес представляет движение лишь нек-рых сортов частиц (напр., в растворах полимеров, в коллоидных растворах). Эту задачу решает разновидность метода молекулярной динамики - броуновская (ланжевеновская) динамика. Суть этого метода состоит в численном интегрировании системы Лан-жевена уравнений, описывающих движение взаимодействующих броуновских частиц и моделирующих взаимодействие броуновских частиц с окружающей средой (напр., с растворителем). Эти ур-ния отличаются от ур-ний Ньютона тем, что их правая часть содержит случайную силу со спектром белого шума и силу трения, пропорциональную скорости частицы. Случайные силы и компоненты тензора трения можно детально изучить с помощью метода молекулярной динамики, описанного ранее. T. о., оба метода молекулярной динамики, применяемые вместе, составляют замкнутый аппарат.

Следующая разновидность метода молекулярной динамики основана на изучении динамики функций распределения координат и импульсов, а не отд. частиц. Это динамич. методы Монте-Карло, суть к-рых состоит в численном интегрировании кинетических уравнений Больцмана (Власова, Фоккера - Планка, Колмогорова) основного кинетич. ур-ния, стохастич. ур-ния Лиу-вилля и т. д. Кинетич. коэффициенты и нек-рые важные свойства функций распределения можно получить при помощи описанного выше M. д. м.

Применения метода молекулярной динамики

Большое число работ посвящено изучению жидкости, в частности модели из твёрдых шаров. Удалось обнаружить фазовый переход типа плавления и получить оценки скорости перемешивания. Mетод молекулярной динамики применяют, в частности, для исследования простых ван-дер-ваальсовых жидкостей. Были определены ур-ние состояния, бинарные и тернарные функции распределения, разл. сведения о микроструктуре, коэф. переноса, получено хорошее согласие с экспериментом. Исследованы ван-дер-ваальсовы одноатомные жидкости и газы в тонких слоях и вблизи адсорбирующих стенок. Смоделированы нек-рые фазовые переходы, адсорбция, образование кластеров и т. д. С помощью разл. модификаций Mетод молекулярной динамики исследовали жидкие металлы для выяснения их структурных и динамич. (транспортных) свойств, а также ур-ний состояний и нек-рых свойств поверхностей металлов. Mетод молекулярной динамики применяют для изучения взаимодействия молекулярных и атомных пучков с поверхностями разл. природы и радиац. повреждений твёрдых тел. Mетод молекулярной динамики позволил исследовать динамику отд. полимерных цепей, растворов и расплавов полимеров, его используют также для исследования биополимеров (белков и нуклеиновых K-T), воды, водных растворов и адсорбции воды, для описания классич. стадии хим. реакций и коагуляции коллоидов, расчёта вязкости в потоке и др.

Литература по методу молекулярной динамики

Знаете ли Вы, что, как ни тужатся релятивисты, CMB (космическое микроволновое излучение) - прямое доказательство существования эфира, системы абсолютного отсчета в космосе, и, следовательно, опровержение Пуанкаре-эйнштейновского релятивизма, утверждающего, что все ИСО равноправны, а эфира нет. Это фоновое излучение пространства имеет свою абсолютную систему отсчета, а значит никакого релятивизма быть не может. Подробнее читайте в FAQ по эфирной физике.