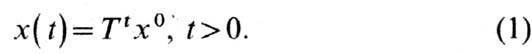
Фазовая траектория в фазовом пространстве. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

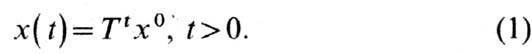
Оператор Т^t удовлетворяет групповому свойству

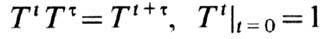
и задаёт однопараметрич. группу преобразований фазового пространства на себя (параметром группы является время t). Группа преобразований фазового пространства, задаваемая оператором Т^t, наз. ф а з о в ы м п о т о к о м. Ф.т. являются орбитами этой группы. Фактически Ф. т. образуется в результате движения фазовой точки x(t)в фазовом пространстве под действием фазового потока. Кривая, начинающаяся в нек-рой нач. точке х⁰ и образованная по закону (1), является, вообще говоря, лишь частью Ф. т. Для получения полной Ф.т. необходимо максимально продолжить кривую (1) не только в область t>0, но и в область t<0.

Ф.т. могут представлять собой: 1) отдельные точки; 2) замкнутые кривые; 3) отрезки кривых конечной длины, заключённые между двумя точками (последние могут принадлежать или не принадлежать траектории); 4) кривые, неограниченные в одну или обе стороны. Траектории, яв- ляющиеся точками, наз. о с о б ы м и т о ч к а м и. Они от- вечают стационарным состояниям динамич. системы и яв- ляются неподвижными точками оператора 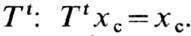Если Ф. т. целиком находится в конечной области фазового пространства, то говорят, что она отвечает ф и н и тн о м у д в и ж е н и ю системы. В противном случае траек-тория представляет и н ф и н и т н о е д в и ж е н и е.

Часто динамич. систему с конечномерным фазовым пространством задают с помощью автономной системы обыкновенных дифференц. ур-ний

где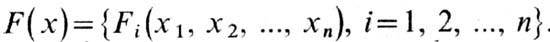

Если в нек-рой области фазового пространства функции F_i(X)непрерывно дифференцируемы, то в этой области различные Ф.т не пересекаются (в силу теоремы единственности решения системы обыкновенных дифференц. ур-ний; см. Коши задача).

Если функции F_i(x)в (2) недифференцируемы где-либо, то Ф.т. могут пересекаться. Напр., динамич. система, задаваемая ур-нием

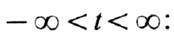
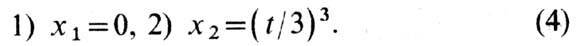
Первая отвечает стационарному состоянию, вторая - ин-финитному движению. Эти две Ф. т. пересекаются в точке x = 0. Неединственность решения обусловлена недифференцируемостью при х = 0 правой части ур-ния (3).

Время движения системы вдоль Ф. т., начинающегося с какой-либо нач. фазовой точки, может быть как бесконечным, так и конечным. Последнее имеет место, напр., в системе

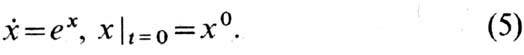
Действительно, из (5) следует

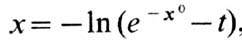так что движение инфинитно, но время эволюции конечно при любых конечных значениях х⁰ и составляет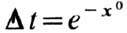

Пусть в фазовом пространстве динамич. системы имеются стационарная точкам к--л. траектории, идущие в эту точку. Пусть также система - гладкая в окрестности особой точки. Тогда время достижения этой точки вдоль любой траектории, не совпадающей с ней, бесконечно. Поэтому стационарные состояния отделены от прочих траекторий.

См. также Динамическая система, Фазовое пространство, Устойчивость движения, Статистическая физика.

Литература по фазовой траектории в фазовом пространстве

Знаете ли Вы, что cогласно релятивистской мифологии "гравитационное линзирование - это физическое явление, связанное с отклонением лучей света в поле тяжести. Гравитационные линзы обясняют образование кратных изображений одного и того же астрономического объекта (квазаров, галактик), когда на луч зрения от источника к наблюдателю попадает другая галактика или скопление галактик (собственно линза). В некоторых изображениях происходит усиление яркости оригинального источника." (Релятивисты приводят примеры искажения изображений галактик в качестве подтверждения ОТО - воздействия гравитации на свет)
При этом они забывают, что поле действия эффекта ОТО - это малые углы вблизи поверхности звезд, где на самом деле этот эффект не наблюдается (затменные двойные). Разница в шкалах явлений реального искажения изображений галактик и мифического отклонения вблизи звезд - 10¹¹ раз. Приведу аналогию. Можно говорить о воздействии поверхностного натяжения на форму капель, но нельзя серьезно говорить о силе поверхностного натяжения, как о причине океанских приливов.
Эфирная физика находит ответ на наблюдаемое явление искажения изображений галактик. Это результат нагрева эфира вблизи галактик, изменения его плотности и, следовательно, изменения скорости света на галактических расстояниях вследствие преломления света в эфире различной плотности. Подтверждением термической природы искажения изображений галактик является прямая связь этого искажения с радиоизлучением пространства, то есть эфира в этом месте, смещение спектра CMB (космическое микроволновое излучение) в данном направлении в высокочастотную область. Подробнее читайте в FAQ по эфирной физике.