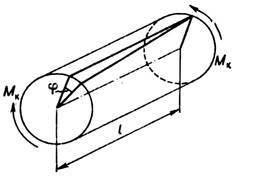
Кручение - деформация стержня, вала и др., характеризующаяся взаимным поворотом поперечных сечений
друг относительно друга вокруг центр. оси стержня под действием крутящих моментов
(пар сил), приложенных к его концам. К. пластинок и оболочек возникает
под действием моментов внутр. касат. сил, появляющихся при их деформации.
Рис. 1. Кручение круглого вала.
Задача о К. круглых стержней
(валов) решается в предположении, что все поперечные сечения стержня в
процессе деформации остаются плоскими, расстояния между поперечными сечениями
не изменяются, а радиусы, проведённые в них, остаются прямыми. В результате
действия крутящихся моментов два поперечных сечения стержня на расстоянии l поворачиваются на угол j (рис. 1), наз. углом закручивания. Угол закручивания,
приходящийся на единицу длины стержня, наз.
относит. углом закручивания
6. В круглых стержнях имеет место свободное (нестеснённое), или чистое, К.,
при к-ром возникают только касат. напряжения. Относит. угол закручивания и касат.
напряжения при чистом К. в упругой стадии работы материала стержня определяются
по ф-лам
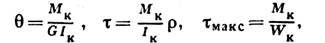
где Мк - крутящий момент, равный сумме крутящих моментов
всех внеш. сил, действующих в рассматриваемом поперечном сечении на условно
отсечённую часть стержня; G - модуль упругости при сдвиге;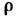
-
расстояние от оси стержня до рассматриваемой точки поперечного сечения; Iк
и WK - момент инерции и момент сопротивления при К., равные
для круглого сечения полярному моменту инерции IP=
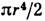и полярному моменту сопротивления Wp=
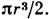Для прямоуг. сечения Iк=
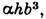WK=
где h и Ь - большая и меньшая стороны сечения;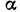 
и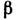 
- коэф.,
зависящие от отношения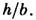 
Для квадратного сечения 
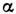=0,14,
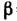=2,2,
при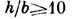 
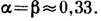В открытых тонкостенных сечениях (уголок, швеллер, двутавр) момент инерции при
К. может приближённо определяться как сумма моментов инерции составляющих их
пластинок: Iк=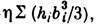
где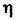 
-
коэф., принимаемый равным 1 для уголков, 1,12 - для швеллеров и 1,2 - для двутавров.
В стержнях некруглого поперечного
сечения К. может быть как нестеснённым (чистым), так и стеснённым (изгибным).
Нестеснённое К. стержня возможно при условии, что во всех его поперечных сечениях
может быть свободная депланация (искажение плоской формы поперечного сечения);
при этом касат. напряжения во всех сечениях будут одинаковыми, а нормальные
напряжения - отсутствовать. В отличие от стержней круглого поперечного сечения,
в к-рых касат. напряжения (рис. 2, а) имеют макс. значение во всех точках контура,
в стержнях прямоуг. сечения макс. касат. напряжения
возникают в середине длинной стороны (рис. 2, б)и определяются по ф-ле
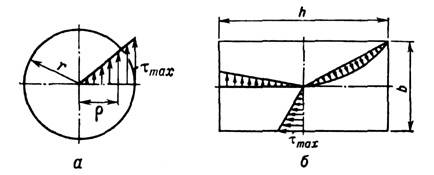
Рис. 2. Распределение касательных
напряжений в упругой стадии работы материала стержней: а - круглого сечения;
б - прямоугольного сечения.
Стеснённое (изгибное) К.
возможно в тех случаях, когда по условиям закрепления или загружения стержня
свободная депланация сечений становится невозможной; при этом появляются дополнит.
нормальные и касательные (секториальные) напряжения.
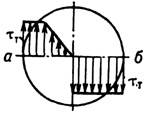
Рис. 3. Распределение касательных напряжений в упругопластической (а) и пластической (б) стадиях.
В упругопластич. стадии
касат. напряжения при К., соответствующие пределу текучести материала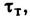
появляются на поверхности
вала (рис. 3, а)и распространяются в сторону его оси. Считают, что в
предельном состоянии пластич. деформации распространяются до оси (рис. 3, б)и при этом не происходит упрочнения материала. Величины предельных крутящих
моментов для стержня круглого сечения определяются по ф-ле Mпр=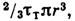
для стержня прямоугольного сечения
Mпр=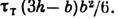
Деформации К. играют существ. роль в работе конструкций и, как правило, являются одной из причин потери устойчивости элементов конструкций.
Л. В. Касабьян
|
|
 |
