Оболочка - твёрдое деформируемое тело, ограниченное двумя криволинейными поверхностями, расстояние между
к-рыми (толщина О.) мало по сравнению с двумя другими размерами. Поверхность,
к-рая делит пополам толщину О., наз. срединной поверхностью; в зависимости
от очертания О. различаются по форме (рис.). О. классифицируются также
по полной кривизне срединной поверхности - т. н. гауссовой кривизне:
положительной - сферические, эллипсоидальные; нулевой - цилиндрические,
конические; отрицательной - гиперболич. параболоиды, тороидальные кругового
или эллипсоидального сечения во внутр. его части. О. могут иметь постоянную
или переменную толщину. В зависимости от материала О. могут быть изотропными
или анизотропными.
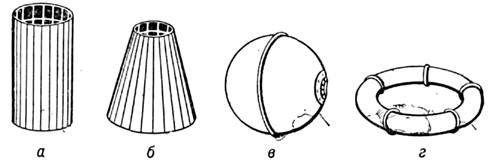
Оболочки различной формы: а - цилиндрическая оболочка кругового сечения; б - коническая; в - сферическая; г - тороидальная.
Под воздействием внеш. нагрузок в О. возникают
внутр. усилия, равномерно распределённые по толщине (т. н. мембранные напряжения
или напряжения в срединной поверхности), и усилия изгиба, образующие в
сечениях О. изгибающие и крутящие моменты, а также поперечные силы. Благодаря
наличию мембранных усилий О. сочетают значит. жёсткость и прочность со
сравнительно малой массой. Если напряжениями изгиба при расчёте О. можно
пренебречь, то её наз. безмоментной. Наличие моментов характерно для участков
О., прилегающих к краям (т. н. краевой эффект), в зонах быстрого изменения
геометрии, вблизи мест приложения сосредоточенных нагрузок. Если напряжения
лежат в пределах пропорциональности для материала О., то для расчёта О.
пользуются зависимостями упругости теории. В статич. расчёте на
прочность и жёсткость определяют напряжения, деформации и перемещения разл.
точек О. в зависимости от заданной нагрузки. Как правило, в расчётах на
прочность прогибы О. (перемещения вдоль нормали к срединной поверхности)
могут считаться малыми по сравнению с толщиной О.; тогда соотношения между
перемещениями и деформациями линейны; соответственно линейными (в упругой
задаче) будут основные дифференц. ур-ния.
При определении несущей способности О.
часто встречаются случаи, когда осн. напряжения лежат за пределами действия
Гука
закона для материала О. Тогда в качестве исходных зависимостей следует
принимать ур-ния пластичности теории. При проектировании конструкций
из О., находящихся в условиях повышенных температур, надо учитывать соотношения
ползучести
теории.
Важным для О. является расчёт на устойчивость
(см. Устойчивость упругих систем ).Специфич. особенность тонкостенных
О. - потеря устойчивости в виде хлопка или прощёлкиваппя, выражающегося
в резком (катастрофич.) переходе от одного устойчивого равновесного состояния
к другому. Этот переход наступает при разл. нагрузках, в зависимости от
нач. несовершенств формы О., нач. напряжений и др. Если рассчитывать О.
на устойчивость с помощью линейных ур-ний (как это принято для стержней
или пластинок), то можно определить лишь т. н. верхнюю критич. нагрузку.
Реальные О. теряют устойчивость часто значительно раньше, в зависимости
от указанных выше факторов. Поэтому уточнённые расчёты на устойчивость
проводятся с помощью геометрически нелинейных зависимостей. Практич. расчёты
должны вестись с учётом эксперим. данных, с их статистич. обработкой. При
проектировании уникальных сооружений из О. - с учётом их устойчивости -
целесообразно проводить предварит. эксперименты над их моделями. Своеобразие
процесса потери устойчивости О. описывается с геом. стороны катастроф
теорией. Для обеспечения устойчивости равновесия О. часто приходится
подкреплять рёбрами, напр. фюзеляжи и крылья летат. аппаратов, нек-рые
типы тонкостенных перекрытий.
В задачах динамики О. рассматриваются
периодич. колебания и нестационарные процессы, связанные с быстрым, или
ударным, нагружением. Раздел теории О., связанный с реакцией выполненных
из нпх конструкций на быстро возрастающую нагрузку, наз. расчётом на динамич.
устойчивость. В отд. случаях несущая способность О., подверженных потере
устойчивости, при быстром нагружении резко возрастает по сравнению со случаем
медленного нагружения. Важным является при этом анализ процесса распространения
упругих волн в материале О.
При обтекании О. потоком жидкости или
газа могут наступить неустойчивые (автоколебательные) режимы, определение
к-рых составляет раздел т. н. гидро- или аэроупругости. К ним относятся
явления классич. и панельного флаттера; наблюдаются также явления срывного
флаттера. Вынужденные колебания О. под действием срывных течений носят
назв. бафтинга. Во мн. разделах динамики О. следует вести расчёт на основании
нелинейных зависимостей. О. широко применяются в качестве покрытий зданий,
в летат. аппаратах, деталях разл. машин и т. д.
Отд. класс О. составляют т. н. мягкие
О., применяемые, напр., для парашютов. Подобные О. не могут иметь сжатых
зон; они являются также безмоментными. При воздействии срывных течений
мягкие О. подвергаются полосканию.
Наряду с металлич. О. в авиации, кораблестроении
и др. областях техники всё более широко применяются О., изготовленные из
композиц. и керамич. материалов. К ним относятся также О., имеющие разл.
строение по толщине, с чередующимися жёсткими слоями и слоями связующего.
Введение композиц. материалов даёт возможность обеспечить необходимую прочность
и жёсткость конструкции при заметно снижающейся массе. Расчёты О., выполненных
из композиц. материалов, а также трёхслойных и многослойных О. представляют
собой отд. разделы общей теории О.
Для расчёта О. как элементов конструкций
наравне с аналитич. методами всё шире применяются самые различные числ.
методы, реализуемые с использованием ЭВМ. Наиб. интенсивно развиваются
методы конечных элементов и метод многоуровневых суперэлементов. Применяются
также метод конечных разностей, метод динамич. программирования и др. Числ.
методы служат для установления напряжённо-деформир. состояния О. и параметров
их устойчивости и динамики. Подобные методы могут быть также приложены
для анализа процесса возникновения и распространения трещин в материале
О. При этом вводятся т. н. сингулярные элементы, отображающие напряжённое
состояние у вершины трещины. Такой анализ может служить для определения
параметров т. н. лавинного процесса распространения трещин, напр. в магистральных
трубопроводах.
А. С. Вольмир
Релятивисты и позитивисты утверждают, что "мысленный эксперимент" весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: "Если факт не соответствует теории - измените факт" (В другом варианте " - Факт не соответствует теории? - Тем хуже для факта").
Максимально, на что может претендовать "мысленный эксперимент" - это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
Понятие "мысленный эксперимент" придумано специально спекулянтами - релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим "честным словом". Подробнее читайте в FAQ по эфирной физике.
