Дифракционная решётка - оптич. элемент, представляющий собой совокупность большого
числа регулярно расположенных штрихов (канавок, щелей, выступов), нанесённых
тем или иным способом на плоскую или вогнутую оптич. поверхность. Д. р. используется
в спектральных приборах в качестве диспергирующей системы для пространственного
разложения эл--магн. излучения в спектр. Фронт световой волны, падающей на Д.
р., разбивается её штрихами на отдельные когерентные пучки, к-рые, претерпев
дифракцию на штрихах, интерферируют (см. Интерференция света), образуя
результирующее пространственное распределение интенсивности света - спектр излучения.
Существуют отражательные
и прозрачные Д. р. На первых штрихи нанесены на зеркальную (металлич.) поверхность,
и результирующая интерференционная картина образуется в отражённом от решётки
свете. На вторых штрихи нанесены на прозрачную (стеклянную) поверхность, и интерференц.
картина образуется в проходящем свете.
Если штрихи нанесены на
плоскую поверхность, то такие Д. р. наз. плоскими, если на вогнутую - вогнутыми.
В современных спектральных приборах используются как плоские, так и вогнутые
Д. р., гл. обр. отражательные.
Плоские отражательные Д. р., изготовляемые с помощью спец. делительных машин с алмазным
резцом, имеют прямолинейные, строго параллельные друг другу и эквидистантные
штрихи одинаковой формы, к-рая определяется профилем режущей грани алмазного
резца. Такая Д. р. представляет собой периодич. структуру с пост. расстоянием
d между штрихами (рис. 1), к-рое наз. периодом Д. р. Различают амплитудные
и фазовые Д. р. У первых периодически изменяется коэфф. отражения или пропускания,
что вызывает изменение амплитуды падающей световой волны (такова решётка из
щелей в непрозрачном экране). У фазовых Д. р. штрихам придаётся спец. форма,
к-рая периодически изменяет фазу световой волны.

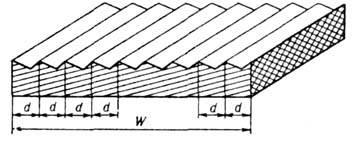
Рис. 1. Схема одномерной
периодической структуры плоской дифракционной решётки (сильно увеличено): d
- период решётки; W - длина нарезной части решётки.
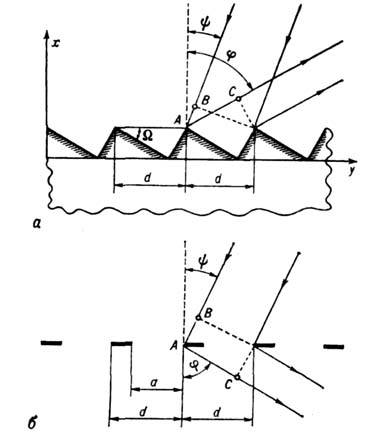
Рис. 2. Схема, иллюстрирующая принцип действия дифракционной решётки: a - фазовой отражательной, б - амплитудной щелевой.
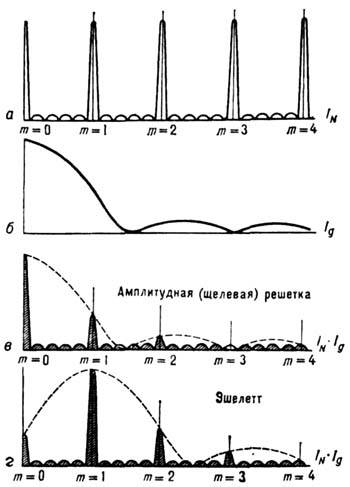
Рис. 3. Интерференционные функции дифракционной решётки.
Если на плоскую Д. р. падает
параллельный пучок света, ось к-рого лежит в плоскости, перпендикулярной к штрихам
решётки, то, как показывает расчёт, получающееся в результате интерференции
когерентных пучков от всех N штрихов решётки пространственное (по углам)
распределение интенсивности света (в той же плоскости) может быть представлено
в виде произведения двух функций: 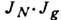 . функция Jg определяется дифракцией света на отд. штрихе, функция
JN обусловлена интерференцией N когерентных пучков,
идущих от штрихов решётки, и связана с периодич. структурой Д. р. функция JN для данной длины волны
. функция Jg определяется дифракцией света на отд. штрихе, функция
JN обусловлена интерференцией N когерентных пучков,
идущих от штрихов решётки, и связана с периодич. структурой Д. р. функция JN для данной длины волны 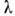 определяется периодом решётки d, полным числом штрихов решётки N и
углами, образованными падающим (угол
определяется периодом решётки d, полным числом штрихов решётки N и
углами, образованными падающим (угол )
и дифрагированным (угол
)
и дифрагированным (угол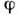 )
пучками с нормалью к решётке (рис. 2), но не зависит от формы штрихов.
Она имеет вид
)
пучками с нормалью к решётке (рис. 2), но не зависит от формы штрихов.
Она имеет вид 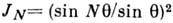 , где
, где 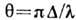 ,
, 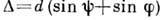 - разность хода между когерентными параллельными пучками, идущими под углом
- разность хода между когерентными параллельными пучками, идущими под углом
 от соседних штрихов
Д.р.:
от соседних штрихов
Д.р.: 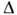 =АВ+АС (см. рис. 2, а - для фазовой отражательной Д. р., 2, б -
для амплитудной щелевой
решётки). функция JN - периодич. функция с резкими интенсивными
гл. максимумами и небольшими вторичными максимумами (рис. 3, а). Между
соседними гл. максимумами расположено N-2
вторичных максимумов
и N-1 минимумов, где интенсивность равна нулю. Положение гл. максимумов
определяется из условия
=АВ+АС (см. рис. 2, а - для фазовой отражательной Д. р., 2, б -
для амплитудной щелевой
решётки). функция JN - периодич. функция с резкими интенсивными
гл. максимумами и небольшими вторичными максимумами (рис. 3, а). Между
соседними гл. максимумами расположено N-2
вторичных максимумов
и N-1 минимумов, где интенсивность равна нулю. Положение гл. максимумов
определяется из условия 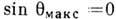 или
или 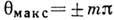 , где m=0,
1, 2, ... - целое число. Откуда
, где m=0,
1, 2, ... - целое число. Откуда
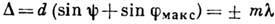
т. е. гл. максимумы образуются
в направлениях, когда разность хода между соседними когерентными пучками равна
целому числу длин волн. Интенсивность всех главных
максимумов одинакова и равна 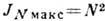 , интенсивность же вторичных максимумов мала и не превышает
, интенсивность же вторичных максимумов мала и не превышает 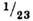 от
от 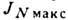 .
.
Соотношение 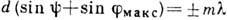 , называемое ур-нием решётки, показывает, что при заданном угле падения
, называемое ур-нием решётки, показывает, что при заданном угле падения 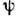 направления на главный максимум
направления на главный максимум 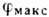 зависят от длины волны
зависят от длины волны 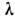 ,
т. е.
,
т. е. 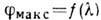 ; следовательно,
Д. р. пространственно (по углам) разлагает излучение разл. длин волн. Если дифрагиров.
излучение, идущее от решётки, направить в объектив, то в его фокальной плоскости
образуется спектр. При этом одновременно образуется неск. спектров при каждом
значении числа
; следовательно,
Д. р. пространственно (по углам) разлагает излучение разл. длин волн. Если дифрагиров.
излучение, идущее от решётки, направить в объектив, то в его фокальной плоскости
образуется спектр. При этом одновременно образуется неск. спектров при каждом
значении числа 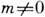 ,
и величина т определяет порядок спектра. При m=0 (нулевой порядок
спектра) спектр не образуется, т. к. условие
,
и величина т определяет порядок спектра. При m=0 (нулевой порядок
спектра) спектр не образуется, т. к. условие 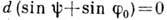 выполняется для всех длин волн (гл. максимумы для всех длин волн совпадают).
Из последнего условия при т=0 также следует, что
выполняется для всех длин волн (гл. максимумы для всех длин волн совпадают).
Из последнего условия при т=0 также следует, что 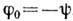 ,
т. е. что направление на максимум нулевого порядка определяется зеркальным отражением
от плоскости решётки (рис. 4); падающий и дифрагированный пучки нулевого порядка
расположены симметрично относительно нормали к решётке. По обе стороны от направления
на максимум нулевого порядка расположены максимумы и спектры m=
,
т. е. что направление на максимум нулевого порядка определяется зеркальным отражением
от плоскости решётки (рис. 4); падающий и дифрагированный пучки нулевого порядка
расположены симметрично относительно нормали к решётке. По обе стороны от направления
на максимум нулевого порядка расположены максимумы и спектры m=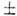 1,
m=
1,
m=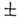 2 и T.
д. порядков.
2 и T.
д. порядков.

Вторая функция Jg, влияющая на результирующее распределение интенсивности в спектре, обусловлена
дифракцией света на отд. штрихе; она зависит от величин 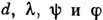 , а также и от формы штриха - его профиля. Расчёт, учитывающий Гюйгенса -
Френеля принцип, даёт для функции Jg выражение
, а также и от формы штриха - его профиля. Расчёт, учитывающий Гюйгенса -
Френеля принцип, даёт для функции Jg выражение
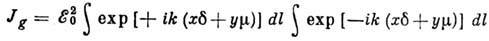 ,
,
где 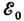 - амплитуда падающей волны,
- амплитуда падающей волны, 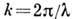 - волновое число;
- волновое число; 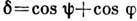 ,
,
 , х и
у - координаты точек на профиле штриха. Интегрирование ведётся по профилю
штриха. Для частного случая плоской амплитудной Д. р., состоящей из узких щелей
в непрозрачном экране (рис. 2, б)или узких отражающих полосок на плоскости,
, х и
у - координаты точек на профиле штриха. Интегрирование ведётся по профилю
штриха. Для частного случая плоской амплитудной Д. р., состоящей из узких щелей
в непрозрачном экране (рис. 2, б)или узких отражающих полосок на плоскости,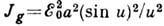 ,
где
,
где 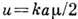 , а - ширина
щелей (или отражающих полосок), и представляет собой дифракц. распределение
интенсивности при дифракции Фраунгофера на щели шириной а (см. Дифракция
света). Вид её приведён на рис. 3 (б). Направление на центр гл. дифракц.
максимума функции Jg определяется из условия u=0 или
, а - ширина
щелей (или отражающих полосок), и представляет собой дифракц. распределение
интенсивности при дифракции Фраунгофера на щели шириной а (см. Дифракция
света). Вид её приведён на рис. 3 (б). Направление на центр гл. дифракц.
максимума функции Jg определяется из условия u=0 или
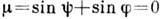 , откуда
, откуда  ,
т. е. это направление определяется зеркальным отражением от плоскости Д. р.,
и, следовательно, направление на центр дифракц. максимума совпадает с направлением
на нулевой - ахроматический - порядок спектра. Следовательно, макс. значение
произведения обеих функций
,
т. е. это направление определяется зеркальным отражением от плоскости Д. р.,
и, следовательно, направление на центр дифракц. максимума совпадает с направлением
на нулевой - ахроматический - порядок спектра. Следовательно, макс. значение
произведения обеих функций 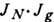 ,
а потому и макс. интенсивность будут в спектре нулевого порядка. Интенсивность
же в спектрах остальных порядков (m
,
а потому и макс. интенсивность будут в спектре нулевого порядка. Интенсивность
же в спектрах остальных порядков (m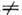 0)
будет соответственно меньше интенсивности в нулевом порядке (что схематически
изображено на рис. 3, в). Это невыгодно при использовании амплитудных
Д. р. в спектральных приборах, т. к. большая часть световой анергии, падающей
на Д. р., направляется в нулевой
порядок спектра, где нет спектрального разложения, интенсивность же спектров
других и даже первого порядков мала.
0)
будет соответственно меньше интенсивности в нулевом порядке (что схематически
изображено на рис. 3, в). Это невыгодно при использовании амплитудных
Д. р. в спектральных приборах, т. к. большая часть световой анергии, падающей
на Д. р., направляется в нулевой
порядок спектра, где нет спектрального разложения, интенсивность же спектров
других и даже первого порядков мала.
Если штрихам Д. р. придать
треугольную несимметричную форму, то у такой фазовой решётки функция Jg
также имеет дифракц. распределение, но с аргументом и, зависящим
от угла наклона 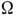 грани штриха (рис. 2, а). При этом направление на центр дифракц.
максимума определяется зеркальным отражением падающего пучка не от плоскости
Д. р., а от грани штриха. Изменяя угол наклона
грани штриха (рис. 2, а). При этом направление на центр дифракц.
максимума определяется зеркальным отражением падающего пучка не от плоскости
Д. р., а от грани штриха. Изменяя угол наклона 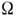 грани
штриха, можно совместить центр дифракц. максимума функции Jg с
любым интерференционным гл. максимумом функции JN любого порядка
m
грани
штриха, можно совместить центр дифракц. максимума функции Jg с
любым интерференционным гл. максимумом функции JN любого порядка
m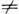 0, обычно
m=1 (рис. 3, г) или m=2. Условие такого совмещения: углы
0, обычно
m=1 (рис. 3, г) или m=2. Условие такого совмещения: углы
 и
и 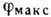 должны одновременно удовлетворять соотношениям
должны одновременно удовлетворять соотношениям 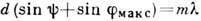 и
и 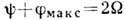 . При этих условиях спектр данного порядка т
. При этих условиях спектр данного порядка т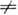 0
будет иметь наиб. интенсивность, а указанные соотношения позволяют определить
необходимую величину
0
будет иметь наиб. интенсивность, а указанные соотношения позволяют определить
необходимую величину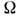 при
заданных
при
заданных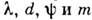 . Фазовые
Д. р. с треугольным профилем штриха, концентрирующие большую часть (до 80 %)
падающего на решётку светового потока в спектр ненулевого порядка, наз. эшелеттами. Угол, под к-рым происходит указанная концентрация падающего светового потока
в спектр, наз. углом блеска Д. р.
. Фазовые
Д. р. с треугольным профилем штриха, концентрирующие большую часть (до 80 %)
падающего на решётку светового потока в спектр ненулевого порядка, наз. эшелеттами. Угол, под к-рым происходит указанная концентрация падающего светового потока
в спектр, наз. углом блеска Д. р.
Осн. спектроскопич. характеристики
Д. р.- угловая дисперсия 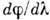 , разрешающая способность
, разрешающая способность  и область дисперсии
и область дисперсии 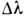 - определяются только свойствами функции JN. связанной с периодич.
структурой Д. р., и не зависят от формы штриха.
- определяются только свойствами функции JN. связанной с периодич.
структурой Д. р., и не зависят от формы штриха.
Угл. дисперсию, характеризующую
степень пространственного (углового) разделения лучей с разной длиной волны,
для Д. р. получают, дифференцируя 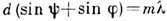 ; тогда
; тогда 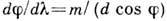 , откуда
следует, что при работе в заданном порядке спектра т величина
, откуда
следует, что при работе в заданном порядке спектра т величина 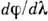 тем больше, чем меньше период решётки. Кроме того, величина
тем больше, чем меньше период решётки. Кроме того, величина 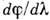 растёт с увеличением угла дифракции
растёт с увеличением угла дифракции 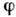 .
Однако в случае амплитудной решётки увеличение угла
.
Однако в случае амплитудной решётки увеличение угла 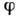 приводит к уменьшению интенсивности спектра. В случае эшелетта можно создать
такой профиль штриха, при к-ром концентрация энергии в спектре будет происходить
при больших углах j, в связи с чем удаётся создавать светосильные спектральные
приборы с большой угл. дисперсией.
приводит к уменьшению интенсивности спектра. В случае эшелетта можно создать
такой профиль штриха, при к-ром концентрация энергии в спектре будет происходить
при больших углах j, в связи с чем удаётся создавать светосильные спектральные
приборы с большой угл. дисперсией.
Теоретическая разрешающая
способность Д. р. 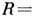
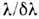 ,
где
,
где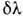 - мин. разность
длин волн двух монохроматич. линий
- мин. разность
длин волн двух монохроматич. линий 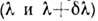 равной интенсивности, к-рые ещё можно различить в спектре. Как у всякого спектрального
прибора, R Д. р. определяется спектральной шириной
равной интенсивности, к-рые ещё можно различить в спектре. Как у всякого спектрального
прибора, R Д. р. определяется спектральной шириной 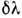 аппаратной функции, к-рой в случае Д. р. являются главные максимумы функции
JN. Определив спектральную ширину
аппаратной функции, к-рой в случае Д. р. являются главные максимумы функции
JN. Определив спектральную ширину 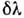 этих максимумов, можно получить выражения для R в виде
этих максимумов, можно получить выражения для R в виде 
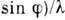 , где W=Nd - полная длина заштрихованной части Д. р. (рис. 1). Из выражения
для R следует, что при заданных углах
, где W=Nd - полная длина заштрихованной части Д. р. (рис. 1). Из выражения
для R следует, что при заданных углах 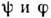 величина R может быть увеличена только за счёт увеличения размеров Д.
р.- W. Величина R возрастает с увеличением угла дифракции
величина R может быть увеличена только за счёт увеличения размеров Д.
р.- W. Величина R возрастает с увеличением угла дифракции  , но медленнее, чем возрастает
, но медленнее, чем возрастает 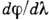 .
Выражение для Л может быть также представлено в виде
.
Выражение для Л может быть также представлено в виде 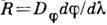 ,
где
,
где 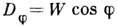 - полная
ширина параллельного дифрагиров. пучка, идущего от Д. р. под углом
- полная
ширина параллельного дифрагиров. пучка, идущего от Д. р. под углом 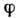 .
.
Область дисперсии Д. р.-
величина спектрального интервала 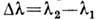 , при к-ром спектр данного порядка т не перекрывается со спектрами соседних
порядков и, следовательно, имеет место однозначная связь между углом дифракции
, при к-ром спектр данного порядка т не перекрывается со спектрами соседних
порядков и, следовательно, имеет место однозначная связь между углом дифракции
 .
. 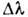 определяется
из условия
определяется
из условия 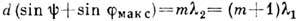 ,
откуда
,
откуда  . Для
m=1
. Для
m=1 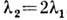 , т.
е. область дисперсии охватывает интервал в одну октаву, напр. всю видимую область
спектра от 800 до 400 нм. Выражение для
, т.
е. область дисперсии охватывает интервал в одну октаву, напр. всю видимую область
спектра от 800 до 400 нм. Выражение для 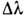 может быть также представлено в виде
может быть также представлено в виде 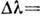
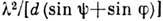 ,
откуда следует, что величина
,
откуда следует, что величина 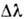 тем больше, чем меньше d, и зависит от угла
тем больше, чем меньше d, и зависит от угла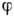 ,
уменьшаясь (в отличие от
,
уменьшаясь (в отличие от 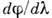 и R) с увеличением
и R) с увеличением 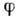 .
.
Из выражений для  и
и 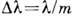 может быть
получено соотношение
может быть
получено соотношение 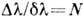 .
Для Д. р. различие между
.
Для Д. р. различие между 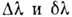 очень большое, т. к. у современных Д. р. полное число штрихов N велико
(N~105 и больше).
очень большое, т. к. у современных Д. р. полное число штрихов N велико
(N~105 и больше).
Вогнутая Д. р. У вогнутых
Д. р. штрихи нанесены на вогнутую (обычно сферическую) зеркальную поверхность.
Такие решётки выполняют роль как диспергирующей, так и фокусирующей системы,
т. е. не требуют применения в спектральных приборах входного и выходного коллиматорных
объективов или зеркал, в отличие от плоских Д. р. При этом источник света (входная
щель S1) и спектр оказываются расположенными на окружности,
касательной к решётке в её вершине, диаметр окружности равен радиусу кривизны
R сферич. поверхности Д. р. (рис. 5). Этот круг наз. кругом
Роуланда. В случае вогнутой Д. р. из источника света (щели) на решётку падает
расходящийся пучок света, а после дифракции на штрихах и интерференции когерентных
пучков образуются результирующие световые волны, сходящиеся на круге Роуланда,
где и располагаются интерференц. максимумы, т. е. спектр. Углы, образованные
осевыми лучами падающего и дифрагированного пучков с осью сферы, связаны соотношением
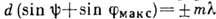 . Здесь также
образуется неск. спектров разл. порядков, расположенных на круге Роуланда, к-рый
является линией дисперсии. Поскольку ур-ние решётки для вогнутой Д. р. такое
же, как и для плоской, то и выражения для спектроскопич. характеристик - угл.
дисперсии, разрешающей способности и области дисперсии - оказываются совпадающими
для решёток обоих видов. Выражения же для линейных дисперсий этих решёток различны
(см. Спектральные приборы).
. Здесь также
образуется неск. спектров разл. порядков, расположенных на круге Роуланда, к-рый
является линией дисперсии. Поскольку ур-ние решётки для вогнутой Д. р. такое
же, как и для плоской, то и выражения для спектроскопич. характеристик - угл.
дисперсии, разрешающей способности и области дисперсии - оказываются совпадающими
для решёток обоих видов. Выражения же для линейных дисперсий этих решёток различны
(см. Спектральные приборы).
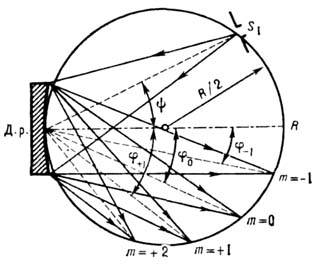
Рис. 5. Схема образования
спектров вогнутой дифракционной решёткой на круге Роуланда.
Вогнутые Д. р., в отличие
от плоских, обладают астигматизмом ,к-рый проявляется в том, что каждая
точка источника (щели) изображается решёткой не в виде точки, а в виде отрезка,
перпендикулярного к кругу Роуланда (к линии дисперсии), т. е. направленного
вдоль спектральных линий, что приводит к значит. уменьшению интенсивности спектра.
Наличие астигматизма также препятствует применению разл. фотометрич. приспособлений.
Астигматизм можно устранить, если штрихи нанести на асферическую, напр. тороидальную
вогнутую, поверхность или нарезать решётку не с эквидистантными, а с изменяющимися
по нек-рому закону расстояниями между штрихами. Но изготовление таких решёток
связано с большими трудностями, они не получили ещё широкого применения.
Топографические Д.
р. В 1970-х гг. был разработан новый, голографический метод изготовления
как плоских, так и вогнутых Д-р., причём у последних астигматизм может быть
устранён в значит. области спектра. В этом методе плоская или вогнутая сферич.
подложка, покрытая слоем спец. светочувствительного материала - фоторезиста, освещается двумя пучками когерентного лазерного излучения (с длиной волны
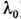 ), в
области пересечения к-рых образуется стационарная интерференц. картина с косинусоидальным
распределением интенсивности (см. Интерференция света), изменяющая
фоторезистный материал в соответствии с изменением интенсивности в картине.
После соответствующей обработки экспонированного фоторезистного слоя и нанесения
на него отражающего покрытия получается голографич. фазовая отражат. решётка
с косинусоидальной формой штриха, т. е. не является эшелеттом и потому обладает
меньшей светосилой. Если освещение производилось параллельными пучками, образующими
между собой угол
), в
области пересечения к-рых образуется стационарная интерференц. картина с косинусоидальным
распределением интенсивности (см. Интерференция света), изменяющая
фоторезистный материал в соответствии с изменением интенсивности в картине.
После соответствующей обработки экспонированного фоторезистного слоя и нанесения
на него отражающего покрытия получается голографич. фазовая отражат. решётка
с косинусоидальной формой штриха, т. е. не является эшелеттом и потому обладает
меньшей светосилой. Если освещение производилось параллельными пучками, образующими
между собой угол 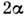 (рис. 6), а подложка плоская, то получается плоская эквидистантная голографич.
Д. р. с периодом
(рис. 6), а подложка плоская, то получается плоская эквидистантная голографич.
Д. р. с периодом 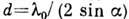 , при сферич. подложке - вогнутая голографич. Д. р., эквивалентная по своим
свойствам обычной нарезной вогнутой решётке. При освещении сферич. подложки
двумя расходящимися пучками от источников, расположенных на круге Роуланда,
получается голографич. Д. р. с криволинейными и неэквидистантными штрихами,
к-рая свободна от астигматизма в значит. области спектра.
, при сферич. подложке - вогнутая голографич. Д. р., эквивалентная по своим
свойствам обычной нарезной вогнутой решётке. При освещении сферич. подложки
двумя расходящимися пучками от источников, расположенных на круге Роуланда,
получается голографич. Д. р. с криволинейными и неэквидистантными штрихами,
к-рая свободна от астигматизма в значит. области спектра.

Рис. 6. Схема изготовления
голографической дифракционной решётки.
Для каждой Д. р. с периодом
d существует предельная длина волны света 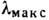 ("красная граница"), для к-рой можно получить спектр ненулевого
порядка. Она определяется из осн. ур-ния решётки
("красная граница"), для к-рой можно получить спектр ненулевого
порядка. Она определяется из осн. ур-ния решётки 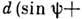
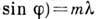 при m=1,
при m=1, 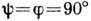 и равна
и равна 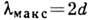 .
Это - теоретич. предел, т. к. работа при углах
.
Это - теоретич. предел, т. к. работа при углах 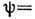
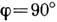 невозможна. Практически Д. р. можно использовать при
невозможна. Практически Д. р. можно использовать при 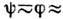 75-80°,
при к-рых
75-80°,
при к-рых 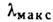 =(1,9-l,95)d.
Поэтому при работе в разл. областях спектра и небольших порядках спектра т используются Д. р. с разл. периодом, а следовательно разл. числом штрихов
на 1 мм: в УФ-области - 3600
=(1,9-l,95)d.
Поэтому при работе в разл. областях спектра и небольших порядках спектра т используются Д. р. с разл. периодом, а следовательно разл. числом штрихов
на 1 мм: в УФ-области - 3600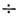 1200
штрих/мм, в видимой области - 1200
1200
штрих/мм, в видимой области - 1200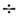 600
штрих/мм, в ИК-области спектра - 300
600
штрих/мм, в ИК-области спектра - 300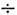 1
штрих/мм. Со стороны коротких длин волн принципиальных ограничений нет, т. к.
ур-ние решётки удовлетворяется и при
1
штрих/мм. Со стороны коротких длин волн принципиальных ограничений нет, т. к.
ур-ние решётки удовлетворяется и при 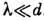 ,
но при высоких порядках спектра. Кроме того, и при
,
но при высоких порядках спектра. Кроме того, и при 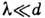 возможна работа в малых порядках, если
возможна работа в малых порядках, если  близки по величине, но разных знаков и ур-ние решётки имеет вид
близки по величине, но разных знаков и ур-ние решётки имеет вид 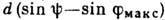 =
= .
.
Нарезные плоские Д. р.
(эшелетты) применяются в широкой области спектра - от 1000 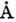 до 1-2 мм, вогнутые - в осн. в области спектра от 10
до 1-2 мм, вогнутые - в осн. в области спектра от 10 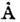 до
1000
до
1000 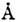 и
обычно при углах
и
обычно при углах 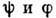 разных знаков и больших величинах самих углов (до 80°). Голографич. вогнутые
Д. р. с компенсиров. астигматизмом используются как в УФ-, так и в видимой областях
спектра.
разных знаков и больших величинах самих углов (до 80°). Голографич. вогнутые
Д. р. с компенсиров. астигматизмом используются как в УФ-, так и в видимой областях
спектра.
Отражательные металлич.
Д. р. (эшелетты) изменяют поляризацию падающего на них света. Это связано с
различием в коэф. отражения световых волн, электрич. вектор к-рых направлен
вдоль штрихов и перпендикулярен к ним.
Качество Д. р. определяется
гл. обр. величиной интенсивности рассеянного света, обусловленного наличием
мелких дефектов на гранях отд. штрихов, и интенсивностью "духов"
- ложных линий, возникающих в спектре в результате нарушения строгой эквидистантности
в расположении штрихов у нарезных Д. р. Преимуществом голографич. Д. р. по сравнению
с нарезными являются отсутствие "духов" и меньшая интенсивность
рассеянного света.
В рентг. области спектра
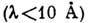 в качестве
Д. р. используют разл. монокристаллы, у к-рых атомы и молекулы,
расположенные в узлах кристаллич. решётки, образуют трёхмерную периодич. структуру
(см. Дифракция рентгеновских лучей).
в качестве
Д. р. используют разл. монокристаллы, у к-рых атомы и молекулы,
расположенные в узлах кристаллич. решётки, образуют трёхмерную периодич. структуру
(см. Дифракция рентгеновских лучей).
Для радиоволн (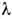 >2
мм) и акустич. волн используют различные проволочные и др. решётки, период к-рых
должен быть соизмерим с длиной волны
>2
мм) и акустич. волн используют различные проволочные и др. решётки, период к-рых
должен быть соизмерим с длиной волны 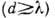 (см. Дифракция волн).
(см. Дифракция волн).
Кроме спектральных приборов
плоские оптич. Д. р.- эшелетты также используются в качестве одного из зеркал
резонаторов лазеров с перестраиваемой частотой генерации.

В. И. Малышев
|
|