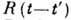 , равной нулю при t<t', а фурье-компонента
, равной нулю при t<t', а фурье-компонента 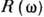 этой функции конечна и потому аналитична в верхней полуплоскости частоты
этой функции конечна и потому аналитична в верхней полуплоскости частоты  . Использование Коши интеграла приводит к простейшему безвычитательному
Д. с. (см. также Гильберта преобразование):
. Использование Коши интеграла приводит к простейшему безвычитательному
Д. с. (см. также Гильберта преобразование):Дисперсионные соотношения - интегральные представления функций отклика, описывающих
реакцию равновесной стационарной физ. системы на внеш. воздействия. Д. с. отражают
аналитич. свойства функций отклика в комплексной плоскости частоты (энергии),
фиксируют их частотную зависимость и приводят к ряду ограничивающих их неравенств,
правил сумм и т. п. В более узком смысле Д. с. связывают рефракцию распространяющихся
в системе волн с их поглощением; сюда же относятся Д. с. для процессов рассеяния
в квантовой механике и квантовой теории поля. Д. с. имеют универсальный вид,
не зависящий от конкретной дииамики системы, и используются во мн. разделах
физики: в динамике диспергирующих сред (отсюда назв. Д. с.), в физике элементарных частиц и др.
Вывод Д. с. не требует
сведений о структуре и динамике системы, а основан на общем причинности принципе: "никакое физ. событие не может повлиять на уже происшедшие события".
Соответственно, реакция системы в момент времени t на воздействие в момент
t' описывается функцией отклика 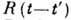 , равной нулю при t<t', а фурье-компонента
, равной нулю при t<t', а фурье-компонента 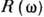 этой функции конечна и потому аналитична в верхней полуплоскости частоты
этой функции конечна и потому аналитична в верхней полуплоскости частоты  . Использование Коши интеграла приводит к простейшему безвычитательному
Д. с. (см. также Гильберта преобразование):
. Использование Коши интеграла приводит к простейшему безвычитательному
Д. с. (см. также Гильберта преобразование):
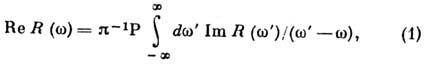
справедливому, если 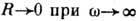 . Здесь P - символ главного значения интеграла. Для полиномиально растущих
с
. Здесь P - символ главного значения интеграла. Для полиномиально растущих
с 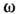 функций
функций 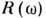 в (1) входит отношение
в (1) входит отношение 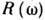 к полиному соответствующей степени
к полиному соответствующей степени 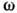 ,
что даёт Д. с. "с вычитаниями"; именно так строятся перенормированные
Д. с. в квантовой теории поля. Реальный вывод Д. с. в большинстве случаев гораздо
сложнее приведённой схемы из-за необходимости учёта ряда факторов: дополнит.
аргументов функции отклика, требований релятивистского принципа причинности ("не
влияют друг на друга также события, связанные пространственноподобным вектором")
и др.
,
что даёт Д. с. "с вычитаниями"; именно так строятся перенормированные
Д. с. в квантовой теории поля. Реальный вывод Д. с. в большинстве случаев гораздо
сложнее приведённой схемы из-за необходимости учёта ряда факторов: дополнит.
аргументов функции отклика, требований релятивистского принципа причинности ("не
влияют друг на друга также события, связанные пространственноподобным вектором")
и др.
Исторически первыми Д.
с. были Крамерса - Кронига соотношения ,связывающие действит. и мнимую
части показателя преломления среды, к-рая обладает частотной дисперсией. Более
общие Д. с., охватывающие и случай пространственной дисперсии, имеют вид (1)
с заменой R величинами
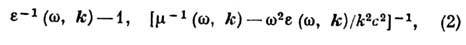
прямо связанными с продольной
и поперечной Грина функциями эл--магн. поля в однородной изотропной среде
(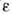 и
и 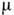 -
диэлектрич. и магн. проницаемости, k - волновой вектор). Д. с. для величины
-
диэлектрич. и магн. проницаемости, k - волновой вектор). Д. с. для величины
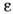 , когда
, когда 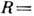
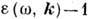 , справедливы лишь в пределе k=0, в к-ром эта величина становится функцией
отклика. Релятивистскому принципу причинности отвечают Д. с., введённые M. А.
Леонтовичем в 1961 и отличающиеся от Д. с. для величин (2) заменой в правой
части
, справедливы лишь в пределе k=0, в к-ром эта величина становится функцией
отклика. Релятивистскому принципу причинности отвечают Д. с., введённые M. А.
Леонтовичем в 1961 и отличающиеся от Д. с. для величин (2) заменой в правой
части 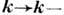
 (
(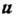 - произвольный
вектор,
- произвольный
вектор,  ). В сочетании
с флуктуационно-диссипативной теоремой, связывающей
). В сочетании
с флуктуационно-диссипативной теоремой, связывающей 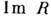 с процессами диссипации в среде, Д. с. дают информацию об общих свойствах последней
(см. также Кубо формулы).
с процессами диссипации в среде, Д. с. дают информацию об общих свойствах последней
(см. также Кубо формулы).
Д. с. для функций Грина важны
также в квантовой теории многих тел и к-вантовой теории поля. Д. с. для фейнмановской
одночастичной функции Грина ферми-системы при T=0 имеет вид (1) с добавлением
фактора 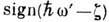 под интегралом,
переходящего в
под интегралом,
переходящего в 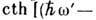
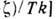 при конечной температуре T,
при конечной температуре T,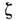 -
хим. потенциал. Д. с. для фейнмановской функции Грина D(z)квантованного
скалярного поля даётся спектральным представлением
-
хим. потенциал. Д. с. для фейнмановской функции Грина D(z)квантованного
скалярного поля даётся спектральным представлением 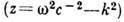 :
:
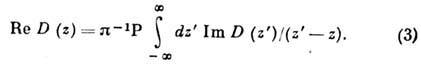
В квантовой теории поля
большое значение имеют также Д. с. для более сложных, чем функции Грина, функций
отклика: формфакторов, амплитуд рассеяния и др. Особую роль играют Д.
с. для амплитуды упругого рассеяния вперёд, связывающие, в силу оптической
теоремы, непосредственно наблюдаемые величины: действит. часть амплитуды
и полное сечение рассеяния. Эксперим. проверка Д. с., выведенных непосредственно
из общих принципов квантовой теории поля, показала применимость этих принципов
вплоть до масштабов ~10-16
см. Д. с. послужили исходным пунктом целого ряда методов описания сильного взаимодействия
(см. Дисперсионных соотношений метод ).Однако они в значит. мере утратили
свою исключит. роль в связи с успехами квантовой хромодинамики как динамич.
теории сильного взаимодействия.

Д. А. Киржниц
Когда тот или иной физик использует понятие "физический вакуум", он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.
Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик Анри Пуанкаре, уже нельзя. Слишком много фактов противоречит этому.
Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование "моря" двух компенсирующих друг друга энергий в вакууме - положительной и отрицательной, а также "моря" компенсирующих друг друга частиц - виртуальных (то есть кажущихся) электронов и позитронов в вакууме.
Однако такая постановка является внутренне противоречивой (виртуальные частицы ненаблюдаемы и их по произволу можно считать в одном случае отсутствующими, а в другом - присутствующими) и противоречащей релятивизму (то есть отрицанию эфира, так как при наличии таких частиц в вакууме релятивизм уже просто невозможен). Подробнее читайте в FAQ по эфирной физике.
|
|