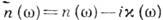 среды с частотной дисперсией, связывающие её показатель преломления n
(
среды с частотной дисперсией, связывающие её показатель преломления n
(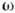 ) н коэф. поглощения
) н коэф. поглощения
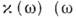 -частота электромагн.
волны):
-частота электромагн.
волны):Крамерса - Кронига соотношения - дисперсионные соотношения для комплексного
показателя преломления 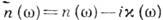 среды с частотной дисперсией, связывающие её показатель преломления n
(
среды с частотной дисперсией, связывающие её показатель преломления n
(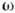 ) н коэф. поглощения
) н коэф. поглощения
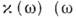 -частота электромагн.
волны):
-частота электромагн.
волны):
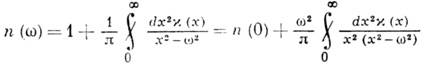
(прямое К.- К. с.);
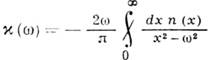
(обратное К.- К. с.). Установлены
X. А. Крамерсом (Н. A. Kramers) и Р. Кронигом (R. Kronig) в 1927. К.- К. с.
отражают аналитичность функции 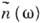 в верх. полуплоскости частоты
в верх. полуплоскости частоты 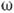 ,
рассматриваемой как комплексная переменная.
,
рассматриваемой как комплексная переменная.
Физически К.- К. с. выражают
существование жёсткой связи дисперсии световой волны (зависимости показателя
преломления н от 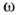 )
и её поглощения. Уже для простейшей среды - идеального атомарного газа с
)
и её поглощения. Уже для простейшей среды - идеального атомарного газа с
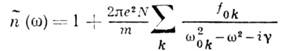
(N - концентрация
атомов, 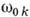 и fok - частота перехода и сила осцилляторов для k-го
атомного уровня, е и т - заряд п масса электрона,
и fok - частота перехода и сила осцилляторов для k-го
атомного уровня, е и т - заряд п масса электрона, 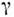 - слабое затухание) вблизи каждой линии перехода обнаруживаются связанные друг
с другом дисперсия и поглощение света. К.- К. с. показывают, что такая связь
существует для любой среды безотносительно к конкретным механизмам дисперсии
и поглощения. В частности, у непоглощающей (прозрачной) во всей области частот
среды не было бы и дисперсии.
- слабое затухание) вблизи каждой линии перехода обнаруживаются связанные друг
с другом дисперсия и поглощение света. К.- К. с. показывают, что такая связь
существует для любой среды безотносительно к конкретным механизмам дисперсии
и поглощения. В частности, у непоглощающей (прозрачной) во всей области частот
среды не было бы и дисперсии.
Будучи частным (и исторически
первым) примером дисперсионных соотношений, К.- К. с. имеют универсальную форму,
не зависящую от структуры и динамики среды. Они выводятся из общего причинности
принципа, применённого к эл--динамич. функциям отклика. Однако поскольку
связь комплексного показателя преломления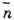 с
этими функциями в общем случае сложна, вывод об аналитичности функции
с
этими функциями в общем случае сложна, вывод об аналитичности функции 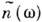 можно сделать не всегда
п соответственно К.- К. с. оказываются справедливыми далеко не для всех типов
сред. Так, в случае однородной изотропной среды с дисперсией пространственной
можно сделать не всегда
п соответственно К.- К. с. оказываются справедливыми далеко не для всех типов
сред. Так, в случае однородной изотропной среды с дисперсией пространственной
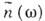 определяется
(неявно) ур-нием
определяется
(неявно) ур-нием
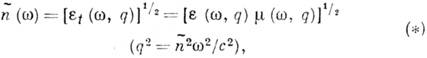
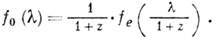
Эквивалентная ширина спектральной
линии 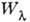 преобразуется при К. с. так же, как и длина волны максимума интенсивности:
преобразуется при К. с. так же, как и длина волны максимума интенсивности: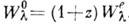 где
где 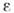 - обычная (продольная),
- обычная (продольная), 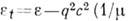 - - 1)/
- - 1)/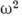 - поперечная диэлектрические проницаемости,
- поперечная диэлектрические проницаемости, 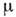 - магн. проницаемость, q - волновой вектор. Хотя функция
- магн. проницаемость, q - волновой вектор. Хотя функция 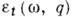 аналитична в верх. полуплоскости ш п не имеет в этой области нулей [они превратились
бы в точки ветвления функции
аналитична в верх. полуплоскости ш п не имеет в этой области нулей [они превратились
бы в точки ветвления функции 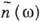 из-за наличия корня в (*)], зависимость
из-за наличия корня в (*)], зависимость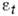 от q усложняет вид функции
от q усложняет вид функции 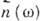 и в общем случае лишает нас информации об её аналитич. свойствах. К.- К. с.
во всяком случае справедливы для любого равновесного немагнитного
и в общем случае лишает нас информации об её аналитич. свойствах. К.- К. с.
во всяком случае справедливы для любого равновесного немагнитного 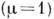 вещества со слабой пространственной дисперсией
вещества со слабой пространственной дисперсией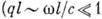 l - характерный внутр. параметр среды размерности длины). В этом случае
l - характерный внутр. параметр среды размерности длины). В этом случае
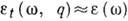 ,
,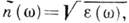 где
где 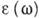 аналитична
в верх. полуплоскости w и не имеет в этой области нулей благодаря условию
аналитична
в верх. полуплоскости w и не имеет в этой области нулей благодаря условию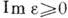
Под К.- К. с. в широком
смысле часто понимаются дисперсионные соотношения для эл--динамич. функции отклика
и связанных с ними величин. Сюда относятся функции 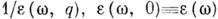 ,
, 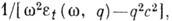 а
также
а
также 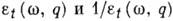 .
У функций
.
У функций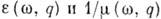 при достаточной силе взаимодействия между частицами среды [когда
при достаточной силе взаимодействия между частицами среды [когда 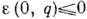 ]
возникает полюс в верх. полуплоскости w, нарушающий дисперсионные соотношения.
Не существует также К.- К. с. и для
]
возникает полюс в верх. полуплоскости w, нарушающий дисперсионные соотношения.
Не существует также К.- К. с. и для 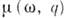 ,
а об аналитич. свойствах функций
,
а об аналитич. свойствах функций 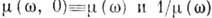 вообще нет информации.
Отсутствие К.- К. с. для перечисленных величин понимается как невозможность
их общего и строгого вывода, что не исключает справедливости этих соотношений
в отдельных частных случаях.
вообще нет информации.
Отсутствие К.- К. с. для перечисленных величин понимается как невозможность
их общего и строгого вывода, что не исключает справедливости этих соотношений
в отдельных частных случаях.
К.- К. с. используются
при теоретич. описании свойств среды и особенностей распространения в ней световой
волны. В практич. плане они дают возможность определить показатель преломления
п(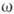 )
по приближённому (эмпирич.) виду коэффициент поглощения
)
по приближённому (эмпирич.) виду коэффициент поглощения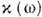

Д. А. Киржниц
|
|