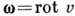 ,
где
,
где 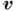 - скорость
жидкости;
- скорость
жидкости; 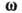 называется
вектором вихря или просто завихренностью.
называется
вектором вихря или просто завихренностью.
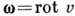 ,
где
,
где 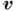 - скорость
жидкости;
- скорость
жидкости; 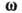 называется
вектором вихря или просто завихренностью.
называется
вектором вихря или просто завихренностью.
Эквивалентной мерой завихренности, более удобной в теоретических
построениях, является антисимметричная часть тензора градиента скорости
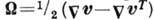 В декартовых координатах x1, х2, x3
связь компонент вектора
В декартовых координатах x1, х2, x3
связь компонент вектора 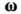 и тензора
и тензора 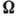 даётся
выражениями
даётся
выражениями
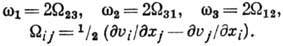
Движение называется безвихревым или потенциальным, если
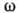 =0, в противном случае
имеет место вихревое движение, возможно, наряду с потенциальным.
=0, в противном случае
имеет место вихревое движение, возможно, наряду с потенциальным.
Векторное поле вихря удобно характеризовать некоторыми геометрическими образами. Вихревой линией называется линия, касательная к которой в каждой точке направлена по вектору вихря; совокупность вихревых линий, проходящих через замкнутую кривую, образует вихревую трубку. Поток вектора вихря через любое сечение вихревой трубки одинаков; он называется интенсивностью вихревой трубки и равен циркуляции скорости Г по произвольному контуру С, однократно охватывающему вихревую трубку (рис. 1),
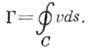
За редкими исключениями движение жидкости или газа почти всегда содержит вихревую компоненту. Так, вихревым является ламинарное течение в круглой трубе, когда скорость распределена по параболическому закону (рис. 2), течение в пограничном слое при плавном обтекании тела и в следе за плохообтекаемым телом, вихревой характер носит любое турбулентное течение. В этих условиях выделение класса вихревых движений оказывается осмысленным, благодаря тому, что при преобладании инерционных сил над вязкими (при очень больших числах Рейнольдса Re) типична локализация завихренности в обособленных массах жидкости - вихрях или вихревых зонах. Примерами вихрей в природе являются смерчи, циклоны: в океанах, в частности, "ринги" Гольфстрима; в атмосферах планет, например, Большое Красное пятно Юпитера, которое представляет собой гигантский вихрь диаметром около 25000 км.
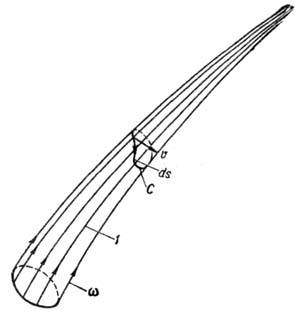
Рис. 1. Вихревая трубка; 1 - вихревая линия.
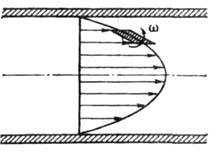
Рис. 2. Вращение элемента жидкости при ламинарном движении в круглой трубе.
Согласно классическим теоремам Гельмгольца, в предельном случае движения невязкой жидкости, плотность которой постоянна или зависит только от давления (в предположении баротропии), в потенциальном силовом поле вихревые линии вморожены в среду, т. е. в процессе движения они состоят из одних и тех же частиц жидкости - являются материальными линиями. Вихревые трубки при этом также оказываются вмороженными в среду, а их интенсивность сохраняется в процессе движения. Сохраняется также циркуляция скорости по любому контуру, состоящему из одних и тех же частиц жидкости (теорема Кельвина). В частности, если при движении область, охватываемая данным контуром, сужается, то интенсивность вращат. движения внутри него возрастает. Это важный механизм концентрации завихренности, реализующийся при вытекании жидкости из отверстия в дне сосуда ("ванны"), при образовании водоворотов вблизи нисходящих потоков в реках и определяющий образование циклонов и тайфунов в зонах пониженного атм. давления, в к-рые происходит подтекание ("конвергенция") воздушных масс.
В жидкости, находившейся в состоянии покоя или потенц. движения, вихри
возникают либо из-за нарушения баротропии, напр. образование кольцевых вихрей при подъёме нагретых масс воздуха - "термиков" (рис. 3), либо из-за взаимодействия с твёрдыми телами.
Если обтекание тела происходит при больших Re, завихренность порождается в узких зонах проявления вязких эффектов - в пограничном слое, а затем сносится в осн. поток, где формирует отчётливо видимые вихри, некоторое время эволюционирующие и сохраняющие свою индивидуальность. Особенно эффектно это проявляется в образовании за плохообтекаемым телом регулярной вихревой дорожки Кармана (рис. 4). Вихреобразование в следе за плохообтекаемым телом определяет осн. часть лобового сопротивления тела, а образование вихрей у концов крыльев летат. аппаратов вызывает дополнительное, т. н. индуктивное сопротивление.
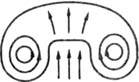
Рис. 3. Образование кольцевого вихря при подъёме термика.
При анализе динамики вихрей
и их взаимодействия с внешним безвихревым потоком часто используется модель
сосредоточенных вихрей - вихревых нитей, представляющих собой вихревые трубки
конечной интенсивности, но бесконечно малого диаметра. Вблизи вихревой нити
жидкость движется относительно неё по окружностям, причём индуцированная скорость
обратно пропорциональна расстоянию от нити,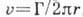 Если ось нити прямолинейна, это выражение верно для любых расстояний от нити
("потенциальный вихрь"). В сечении нормальной плоскостью это течение
соответствует точечному вихрю. Система точечных вихрей образует консервативную
динамич. систему с конечным числом степеней свободы, во многом аналогичную системе
взаимодействующих частиц. Сколь угодно малое возмущение первоначально прямолинейных
вихревых нитей приводит к их искривлению с бесконечными скоростями. Поэтому
в расчётах их заменяют вихревыми трубками конечной завихренности. Узкая область
завихренности, разделяющая две протяжённые области безвихревого движения, моделируется с помощью понятия
Если ось нити прямолинейна, это выражение верно для любых расстояний от нити
("потенциальный вихрь"). В сечении нормальной плоскостью это течение
соответствует точечному вихрю. Система точечных вихрей образует консервативную
динамич. систему с конечным числом степеней свободы, во многом аналогичную системе
взаимодействующих частиц. Сколь угодно малое возмущение первоначально прямолинейных
вихревых нитей приводит к их искривлению с бесконечными скоростями. Поэтому
в расчётах их заменяют вихревыми трубками конечной завихренности. Узкая область
завихренности, разделяющая две протяжённые области безвихревого движения, моделируется с помощью понятия

Рис. 4. Фотография вихревой
дорожки Кармана за движущимся цилиндром.
В вязкой жидкости происходит выравнивание - "диффузия" локализованной завихренности, причём скорость
диффузии определяет кинематическая вязкость жидкости
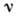 ,
имеющая размерность циркуляции скорости [m2/s]. При этом эволюция
завихренности определяется уравнением
,
имеющая размерность циркуляции скорости [m2/s]. При этом эволюция
завихренности определяется уравнением
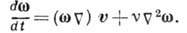
При больших Re движение турбулизуется, и "диффузия завихренности" определяется много большим коэффициентом эффективной турбулентной вязкости, не являющимся константой жидкости и сложным образом зависящим от характера движения. Ввиду того, что крупные вихри в значительной мере определяют перенос на большие расстояния примеси в атмосфере и океане, динамика турбулентных вихрей - одна из наиболее интенсивно изучаемых нерешённых задач гидродинамики.

В. M. Ентов.
|
|