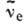 :
:Бета-распад ядер атомов (β‑распад) - один из 3 основных типов
радиоактивности.
При электронном β‑распаде один из нейтронов ядра превращается в протон с испусканием электрона и
электронного антинейтрино
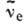 :
:
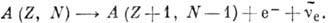
Здесь А - массовое число, Z - заряд
ядра, N - число нейтронов. При позитронном β‑распаде один из
протонов ядра превращается в нейтрон с испусканием позитрона и электронного
нейтрино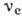 :
:
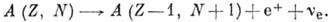
С бета-распадом тесно связаны так называемые обратные β-процессы:
захват электрона с К-оболочки атома (К-захват) или менее вероятный
захват с L- и др. оболочек (электронный захват:)
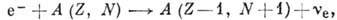
а также обратный β‑распад:
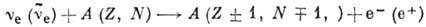
(подробнее см. Нейтрино).
Бета-распад возможен в том случае, когда разность масс начального
N и конечного 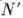 ядер превышает сумму масс электрона mе и нейтрино
ядер превышает сумму масс электрона mе и нейтрино 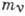 .
Всегда, когда энергетически возможен β‑распад, возможен и электронный
захват. В ряде случаев может происходить т. н. двойной
бета-распад:
.
Всегда, когда энергетически возможен β‑распад, возможен и электронный
захват. В ряде случаев может происходить т. н. двойной
бета-распад:
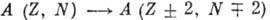
с испусканием двух β‑частиц и нейтринной пары либо без испускания нейтрино.
Энергия, выделяющаяся при бета-распаде, распределяется
между электроном, нейтрино и конечным ядром; подавляющая часть приходится на
долю лёгких частиц. Поэтому спектр испускаемых β‑частиц непрерывен, их кинетич. энергия принимает значения от 0 до нек-рой граничной
энергии 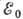 , определяемой
соотношением
, определяемой
соотношением
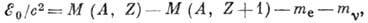
где M - массы начального и конечного
ядер.
В 1956 Ли Цзундао и Ян Чжэньнин (США, [1]) предположили, что в слабых
взаимодействиях, обусловливающих бета-распад, закон сохранения пространственной
чётности может нарушаться. Для проверки этой гипотезы предлагалось измерить
угловые распределения электронов и позитронов при бета-распаде поляризованных
ядер. При несохранении пространственной чётности угловое распределение электронов должно быть асимметрично-относительно
направления спина ядра. Впервые такой эксперимент выполнен в 1956 By Цзяньсюн
с сотрудниками (США) на поляризов. ядрах 60Co, была обнаружена сильная
асимметрия - электроны испускались в направлении, противоположном спину ядра
[2].
Нарушение сохранения пространственной
чётности в бета-распаде должно приводить также к отличию от О ср. значений продольных
поляризаций β‑частиц и нейтрино. Эксперименты показали, что при бета-распаде
рождаются электроны со спинами, антипараллельными их импульсу (левовинтовые), и позитроны со спинами, параллельными
импульсу (правовинтовые), причём для большинства 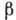 -переходов
степени их поляризации равны
-переходов
степени их поляризации равны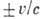 Если
Если 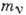 =0, то испускаемые
в бета-распаде нейтрино и антинейтрино должны иметь определ. значение проекции, спина
на направление импульса (спиральность ),т. е. обладать 100%-ной продольной
поляризацией. Оказалось, что при β‑распаде
испускаются левополяризов. нейтрино, а в β‑распаде - правополяризов. антинейтрино.
=0, то испускаемые
в бета-распаде нейтрино и антинейтрино должны иметь определ. значение проекции, спина
на направление импульса (спиральность ),т. е. обладать 100%-ной продольной
поляризацией. Оказалось, что при β‑распаде
испускаются левополяризов. нейтрино, а в β‑распаде - правополяризов. антинейтрино.
Основы теории бета-распада. созданы в 1934 Э. Ферми [3]. Он исходил из 4-фермионного взаимодействия нуклонов и лептонов по аналогии с эффективным электрон-нуклонным взаимодействием в электродинамике
(рис. 1, а). Однако, в отличие от электромагнитного взаимодействия, к-рое
является дальнодействующим, 4-фермионное взаимодействие Ферми был"
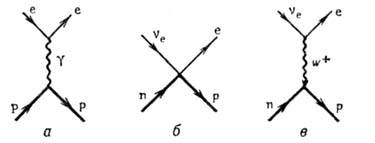
Рис. 1. Схематическое
изображение (Фейнмана диаграммы): а - электромагнитного взаимодействия; б - бета-распада в теории
Ферми; в - в современной теории электрослабого взаимодействия.
контактным (локальным; рис. 1, б).
Гамильтониан нуклон-лептонного взаимодействия Ферми имел вид:
 (1)
(1)
Здесь 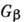 - константа взаимодействия (константа Ферми),
- константа взаимодействия (константа Ферми), 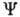 - 4-компонентные волновые функции взаимодействующих частиц, удовлетворяющие Дирака
уравнению,
- 4-компонентные волновые функции взаимодействующих частиц, удовлетворяющие Дирака
уравнению, 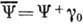 - сопряжённые волновые функции,
- сопряжённые волновые функции, 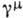 - дираковские матрицы,
- дираковские матрицы, 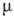 =0,
1, 2, 3, 4;
=0,
1, 2, 3, 4;  ;
;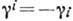 0=1, 2, 3).
0=1, 2, 3).
В первонач. варианте теории Ферми нуклон-лептонное
взаимодействие имело чисто векторную форму. Впоследствии было выяснено, что
гамильтониан слабого взаимодействия может быть комбинацией релятивистски-инвариантных
слагаемых, образованных из скаляра (S), псевдоскаляра (P), вектора
(F), аксиального вектора (А) и тензора (T). Открытие несохранения
пространственной чётности, исследование корреляций между направлениями вылета
β‑частиц и нейтрино при Б,-р. ядер 35Ar и 6He, а также угловых
распределений электронов и нейтрино при распаде
поляризованных нейтронов
показали, что в бета-распаде реализуется главным образом F-А-вариант
(см. Бета-распад
нейтрона).
Эффективный гамильтониан бета-распада, используемый
в совр. расчётах, предложен P. Ф. Фейнманом и M. Гелл-Маном в 1958 [4]. Он имеет
вид:
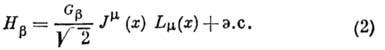
Здесь 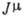 -
нуклонный ток,
-
нуклонный ток, 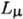 -
лептонный ток (см. Ток в квантовой теории поля), х - пространственно-временная
координата; через э. с. обозначены эрмитово-сопряжённые члены;
-
лептонный ток (см. Ток в квантовой теории поля), х - пространственно-временная
координата; через э. с. обозначены эрмитово-сопряжённые члены; 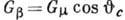 , где
, где 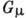 - универсальная
константа слабого взаимодействия; множитель
- универсальная
константа слабого взаимодействия; множитель 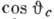 отвечает процессам без изменения странности (
отвечает процессам без изменения странности (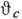 -т.
н. Кабиббо угол ).Константа
-т.
н. Кабиббо угол ).Константа 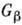 =1,40*10-49
эрг*см3 была найдена экспериментально (см. ниже). Лептонный
ток
=1,40*10-49
эрг*см3 была найдена экспериментально (см. ниже). Лептонный
ток 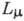 является
комбинацией V- и А- слагаемых с равными весами и может быть выражен
через волновые функции электрона и нейтрино:
является
комбинацией V- и А- слагаемых с равными весами и может быть выражен
через волновые функции электрона и нейтрино:
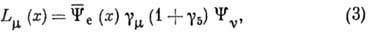
где 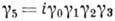 . Нуклонный ток
. Нуклонный ток 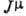 также является комбинацией векторного и аксиально-векторного слагаемых
также является комбинацией векторного и аксиально-векторного слагаемых 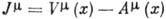 .
Он не может быть выписан в явном виде через волновые функции нуклонов, однако
матричные элементы от
.
Он не может быть выписан в явном виде через волновые функции нуклонов, однако
матричные элементы от 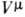 и
и 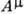 между нуклонными
состояниями, к-рые определяют характеристики бета-распада (см. ниже), могут быть выражены
через небольшое число констант связи
между нуклонными
состояниями, к-рые определяют характеристики бета-распада (см. ниже), могут быть выражены
через небольшое число констант связи 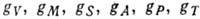 :
:
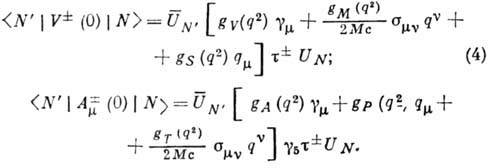
Здесь N, N'- исходный
и конечный нуклоны; U - дпраковский биспинор (решение свободного ур-ния
Дирака), 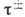 -повышающий
и понижающий изоспиновые операторы, переводящие нейтрон в протон и протон в
нейтрон (см. Изотопический спин;)
-повышающий
и понижающий изоспиновые операторы, переводящие нейтрон в протон и протон в
нейтрон (см. Изотопический спин;)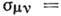
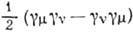 ,
, 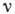 =
0, 1, 2, 3;
=
0, 1, 2, 3; 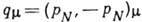 - передаваемый 4-импульс, рN'
и рN - импульсы начального и конечного состояний нуклона.
- передаваемый 4-импульс, рN'
и рN - импульсы начального и конечного состояний нуклона.
Из гипотезы сохранения векторного
тока следует, что 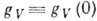 =1,
=1, 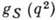 =0, gM(0)=
=0, gM(0)=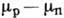 =3,70,
где mр
и mn
- аномальные магн. моменты протона и нейтрона в единицах ядерного магнетона
(см. Магнетизм микрочастиц ).Эксперим. исследования бета-распада позволили подтвердить
гипотезу векторного тона сохранения и получить ограничение на константу
gT, характеризующую т. н. аксиальный ток второго рода:
=3,70,
где mр
и mn
- аномальные магн. моменты протона и нейтрона в единицах ядерного магнетона
(см. Магнетизм микрочастиц ).Эксперим. исследования бета-распада позволили подтвердить
гипотезу векторного тона сохранения и получить ограничение на константу
gT, характеризующую т. н. аксиальный ток второго рода:
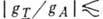 10-4.
10-4.
Выделяемые при бета-распаде энергии малы по
сравнению с 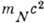 (mN
-масса нуклона), поэтому можно считать передаваемый 4-импульс
(mN
-масса нуклона), поэтому можно считать передаваемый 4-импульс 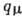 равным О. При этом однонуклонный гамильтониан
равным О. При этом однонуклонный гамильтониан 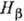 примет вид:
примет вид:
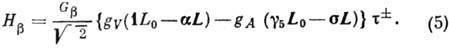
Здесь 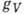 и
и 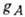 -векторная
и аксиальная константы нуклон-лептонного взаимодействия, 1 - единичный оператор,
-векторная
и аксиальная константы нуклон-лептонного взаимодействия, 1 - единичный оператор,
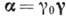 - матрицы Дирака,
- матрицы Дирака,
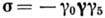 -спиновые матрицы
Паули. T. о., эффективный гамильтониан бета-распада определяется в осн. двумя константами
связи - векторной
-спиновые матрицы
Паули. T. о., эффективный гамильтониан бета-распада определяется в осн. двумя константами
связи - векторной 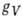 и аксиально-векторной
и аксиально-векторной 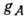 .
.
Дальнейшее развитие теории привело к
созданию единой теории слабых и эл--магн. взаимодействий (см. Электрослабое
взаимодействие). Согласно этой теории, слабое взаимодействие не является
локальным, а происходит путём обмена заряженными 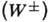 и нейтральными (Z0) векторными частицами массой около 100 Гэв/с2
(рис. 1, в). Однако на теории бета-распада существование этих частиц практически
не сказывается из-за малости
и нейтральными (Z0) векторными частицами массой около 100 Гэв/с2
(рис. 1, в). Однако на теории бета-распада существование этих частиц практически
не сказывается из-за малости 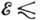 10 МэВ по сравнению с
10 МэВ по сравнению с 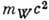 .
По этой причине теория электрослабых взаимодействий для бета-распада сводится к теории
Фейнмана - Гелл-Мана.
.
По этой причине теория электрослабых взаимодействий для бета-распада сводится к теории
Фейнмана - Гелл-Мана.
Для вычисления наблюдаемых характеристик β‑распад-периодов полураспада 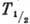 ,
формы
,
формы 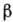 -спектров,
-спектров,
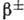 -
-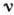 -угловых
корреляций и др. необходимо знать амплитуду процесса, определяемую матричным
элементом перехода между начальным i и конечным f ядерными состояниями:
-угловых
корреляций и др. необходимо знать амплитуду процесса, определяемую матричным
элементом перехода между начальным i и конечным f ядерными состояниями: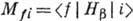 .
.
В случае бета-распада нуклона: 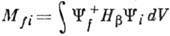
В случае бета-распада ядер:
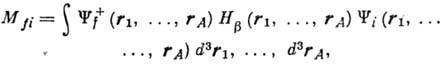
где эффективный гамильтониан процесса
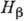 равен сумме слагаемых, описывающих бета-распад отдельных, составляющих ядро нуклонов:
равен сумме слагаемых, описывающих бета-распад отдельных, составляющих ядро нуклонов:
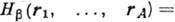
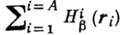 . Здесь r - пространственная координата нуклонов в ядре. Это не означает,
что теория может описывать только однонуклонные переходы; эффекты многонуклонной
структуры, включая возможность коллективных возбуждений ядра, учитываются
в волновых функциях начального и конечного состояний ядер.
. Здесь r - пространственная координата нуклонов в ядре. Это не означает,
что теория может описывать только однонуклонные переходы; эффекты многонуклонной
структуры, включая возможность коллективных возбуждений ядра, учитываются
в волновых функциях начального и конечного состояний ядер.
Однако в таком приближении не учитываются
т. н. мезонные обменные токи, описывающие испускание пары 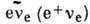 виртуальными мезонами, к-рыми обмениваются нуклоны в ядре (рис. 2, а), а также
испускание лептонной пары нуклонами, происходящее за счёт обмена виртуальными
мезонами (рис. 2, б, в). Учёт мезонных обменных токов приводит к тому,
что
виртуальными мезонами, к-рыми обмениваются нуклоны в ядре (рис. 2, а), а также
испускание лептонной пары нуклонами, происходящее за счёт обмена виртуальными
мезонами (рис. 2, б, в). Учёт мезонных обменных токов приводит к тому,
что 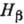 становится
многочастичным оператором. Вклады
становится
многочастичным оператором. Вклады
Рис. 2. Примеры вкладов
мезонных обменных токов в амплитуду бета-распада: а - рождение лептонной пары
при бета-распаде виртуального мезона (напр., 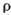 -
или
-
или  -мезонов в
-мезонов в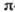 -мезон),
N1 и N2-нуклоны до процесса, N1' и N2'-после: б -рождение лептонной пары нуклоном
при испускании мезона, поглощаемого другим нуклоном ядра; в-виртуальное
возбуждение нуклонного резонанса (
-мезон),
N1 и N2-нуклоны до процесса, N1' и N2'-после: б -рождение лептонной пары нуклоном
при испускании мезона, поглощаемого другим нуклоном ядра; в-виртуальное
возбуждение нуклонного резонанса (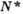 или
или 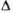 ) при обмене
мезоном с другим нуклоном и последующий бета-распад резонанса.
) при обмене
мезоном с другим нуклоном и последующий бета-распад резонанса.
мезонных обменных токов в b-спектры
и периоды полураспада могут достигать неск. %.
Спектр β‑частиц связан с матричным элементом 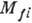 соотношением:
соотношением:
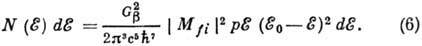
Здесь р и 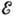 -импульс
и энергия испускаемой β‑частицы.
При выводе (6) предполагалось, что
-импульс
и энергия испускаемой β‑частицы.
При выводе (6) предполагалось, что 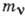 =0
и энергия отдачи конечного ядра пренебрежимо мала по сравнению с
=0
и энергия отдачи конечного ядра пренебрежимо мала по сравнению с 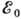 .
Если
.
Если 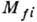 не зависит
от энергии, форма
не зависит
от энергии, форма 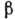 -спектра
определяется только "статистич." множителем:
-спектра
определяется только "статистич." множителем: 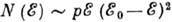 .
.
При расчёте 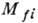 используется ряд приближений: 1) граничные энергии
используется ряд приближений: 1) граничные энергии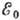 относительно малы, вследствие чего длины волн де Бройля испускаемых лептонов
велики по сравнению с размерами R ядер:
относительно малы, вследствие чего длины волн де Бройля испускаемых лептонов
велики по сравнению с размерами R ядер: 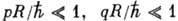 ,
т. е. волновые функции лептонов незначительно меняются внутри ядра; 2) будучи
взяты между ядерными состояниями, нек-рые входящие в ф-лу для
,
т. е. волновые функции лептонов незначительно меняются внутри ядра; 2) будучи
взяты между ядерными состояниями, нек-рые входящие в ф-лу для 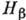 операторы имеют матричные элементы порядка 1, тогда как другие имеют матричные
элементы порядка
операторы имеют матричные элементы порядка 1, тогда как другие имеют матричные
элементы порядка 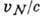 ,
где
,
где 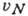 - характерная
скорость нуклона в ядре. Для лёгких и средних ядер параметр
- характерная
скорость нуклона в ядре. Для лёгких и средних ядер параметр 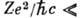 1.
При вычислении
1.
При вычислении 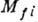 обычно используется разложение по этим малым параметрам.
обычно используется разложение по этим малым параметрам.
Волновая функция нейтрино 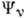 ,
входящая в лептонную часть матричного элемента
,
входящая в лептонную часть матричного элемента 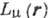 , описывается плоской волной:
, описывается плоской волной: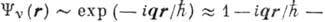
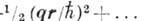 . T. к.
. T. к. 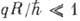 ,
то внутри ядра (r < R)Yn
(r)yconst,
и при интегрировании по объёму ядра нейтринная волновая функция не приводит к
зависимости
,
то внутри ядра (r < R)Yn
(r)yconst,
и при интегрировании по объёму ядра нейтринная волновая функция не приводит к
зависимости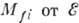 .
.
Если пренебречь взаимодействием испускаемой β‑частицы с
кулоновскими полями ядра и электронной оболочки атома, то её волновая функция
также будет описываться плоской волной: 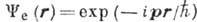 .
.
Учёт кулоновского взаимодействия приводит
к отличию волновой функции β‑частицы
от плоской волны; в результате волновая функция становится зависящей от энергии
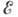 даже при
даже при 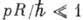 . Влияние кулоновского взаимодействия испускаемых β‑частиц
на их энергетич. спектр учитывается с помощью т. н. кулоновского поправочного
фактора, или функции Ферми
. Влияние кулоновского взаимодействия испускаемых β‑частиц
на их энергетич. спектр учитывается с помощью т. н. кулоновского поправочного
фактора, или функции Ферми 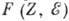 ,
к-рая при
,
к-рая при 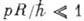 определяется
как квадрат отношения волновых функций β‑частицы,
вычисленных с учётом (ZK0)
и без учёта (Z=0) кулоновского поля ядра в центре (r =0) или на периферии
(r= R)ядра:
определяется
как квадрат отношения волновых функций β‑частицы,
вычисленных с учётом (ZK0)
и без учёта (Z=0) кулоновского поля ядра в центре (r =0) или на периферии
(r= R)ядра:
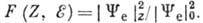
Приближение, в к-ром учитываются лишь
главные нуклонные вклады в гамильтониан 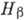 ,
а лептонные волновые функции внутри ядра считаются не зависящими от координат,
наз. разрешённым. В этом приближении выражение для спектра β‑частиц принимает вид:
,
а лептонные волновые функции внутри ядра считаются не зависящими от координат,
наз. разрешённым. В этом приближении выражение для спектра β‑частиц принимает вид:
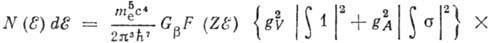
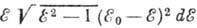 . (7)
. (7)
Здесь энергия выражена в единицах 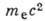 (те- масса электрона);
(те- масса электрона);
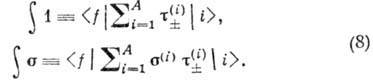
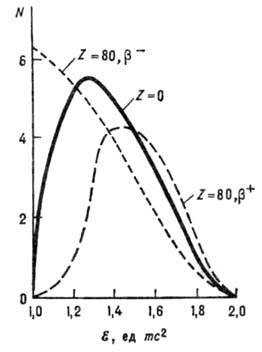
Рис. 3. Энергетические
спектры разрешенных переходов с кулоновской поправкой для Z = 80 и Z=0 для
переходов с кулоновской поправкой для Z = 80 и Z=0 для  1
МэВ; в случае Z=0 b-
и b+-спектры
совпадают. По оси абсцисс отложена полная энергия
1
МэВ; в случае Z=0 b-
и b+-спектры
совпадают. По оси абсцисс отложена полная энергия электрона.
электрона.
Кулоновское поле ядра увеличивает вероятность испускания электронов и
уменьшает вероятность испускания позитронов в области низких энергий. Кроме
того, при учёте кулоновского фактора F (Z,
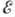 )
вероятность испускания электрона при бета-распаде на нижней границе
)
вероятность испускания электрона при бета-распаде на нижней границе
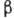 -спектра
не обращается в нуль, а стремится к конечному значению (рис. 3). Влияние кулоновского
фактора на
-спектра
не обращается в нуль, а стремится к конечному значению (рис. 3). Влияние кулоновского
фактора на 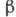 -спектры
и вероятность бета-распада возрастают с увеличением Z и уменьшением
-спектры
и вероятность бета-распада возрастают с увеличением Z и уменьшением
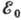 .
При расчётах F (Z,
.
При расчётах F (Z,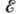 )
необходимо учитывать также экранирование заряда ядра атомными электронами (особенно
важно в случае β‑распада)
[9].
)
необходимо учитывать также экранирование заряда ядра атомными электронами (особенно
важно в случае β‑распада)
[9].
Полная вероятность W бета-распада в единицу времени может быть
получена интегрированием N (e) по энергии: 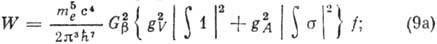
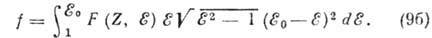
Если пренебречь взаимодействием испускаемой β‑частицы с кулоновским полем атома, то:
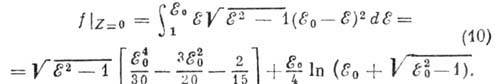
В общем случае f вычисляется с помощью табулированных значений F (Z, ).
).
T. к. период полураспада 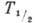 связан с вероятностью Б.-p. W соотношением
связан с вероятностью Б.-p. W соотношением 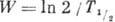 ,
то
,
то
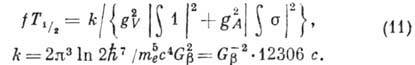
В правой стороне последнего равенства
 в единицах 10-49 эрг*см3. Величина
в единицах 10-49 эрг*см3. Величина 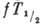 ,
называемая сравнит. периодом полураспада, играет существ. роль в классификации
,
называемая сравнит. периодом полураспада, играет существ. роль в классификации
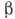 -переходов. Функция
f учитывает зависимость вероятности бета-распада от
-переходов. Функция
f учитывает зависимость вероятности бета-распада от 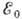 и кулоновских эффектов; поэтому
и кулоновских эффектов; поэтому 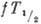 , в отличие от
, в отличие от 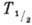 ,
зависит только от
,
зависит только от 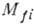 .
.
Бета-распад характеризуется широким диапазоном изменения периодов
полураспада T1/2 -от 10-2 с до 1016
лет. Такая большая вариация величин T1/2 объясняется 2 осн. причинами: 1) период полураспада сильно зависит от 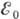 (при
(при 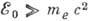 , W ~
, W ~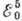 ),
а
),
а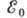 изменяется в
широких пределах от 2,64 кэВ для перехода
изменяется в
широких пределах от 2,64 кэВ для перехода до 13,43 МэВ для
до 13,43 МэВ для  ;
2) в зависимости от спинов и чётностей начального и конечного ядерных состояний
вклад в амплитуду процесса дают разл. слагаемые в эффективном гамильтониане
бета-распада, матричные элементы к-рых имеют разный порядок величины. Кроме того, испускаемая
при бета-распаде лептонная пара может уносить разл. орбитальный момент. С увеличением
этого момента из-за центробежного эффекта уменьшаются значения волновых функций
лептонов во внутриядерной области, а следовательно, и интеграл перекрытия волновых
функций, определяющий
;
2) в зависимости от спинов и чётностей начального и конечного ядерных состояний
вклад в амплитуду процесса дают разл. слагаемые в эффективном гамильтониане
бета-распада, матричные элементы к-рых имеют разный порядок величины. Кроме того, испускаемая
при бета-распаде лептонная пара может уносить разл. орбитальный момент. С увеличением
этого момента из-за центробежного эффекта уменьшаются значения волновых функций
лептонов во внутриядерной области, а следовательно, и интеграл перекрытия волновых
функций, определяющий 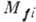 .
В соответствии с этим все
.
В соответствии с этим все 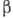 -переходы
разделяются на разрешённые и запрещённые.
-переходы
разделяются на разрешённые и запрещённые.
Разрешённые переходы. T. к. в разрешённом
приближении волновые функции лептонов внутри ядра постоянны, то лептоны не уносят
орбитального углового момента. Если при этом спин ядра не меняется, то суммарный
спин, уносимый лептонной парой, также равен 0. Такие переходы наз. фермиевскими.
Если же векторное изменение спина ядра (суммарный спин, уносимый лептонной парой)
равно 1, переходы наз. гамов-теллеровскими. Чётность ядерных состояний в разрешённых
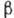 -переходах не
меняется. T. о., отбора правила ,ограничивающие изменение полного момента
I и чётности я ядра, в случае разрешённых переходов фермиевского
-переходах не
меняется. T. о., отбора правила ,ограничивающие изменение полного момента
I и чётности я ядра, в случае разрешённых переходов фермиевского 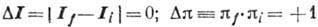 типа имеют вид:
типа имеют вид:
Для гамов-теллеровских переходов правила
отбора имеют вид: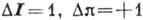 .
.
Разрешённые переходы подразделяются
на сверх-разрешённые и затруднённые. К первым относятся переходы между ядерными
состояниями, имеющими сходные волновые функции, вследствие чего интегралы
их перекрытия велики ( 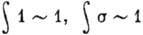 ) ,
) ,
а величины 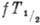 принимают
миним. значения. К сверх-разрешённым переходам относятся, в частности, переходы
между состояниями, принадлежащими одному и тому же изомультиплету (т. е. между
аналоговыми состояниями ядер). Для сверхразрешённых
принимают
миним. значения. К сверх-разрешённым переходам относятся, в частности, переходы
между состояниями, принадлежащими одному и тому же изомультиплету (т. е. между
аналоговыми состояниями ядер). Для сверхразрешённых 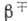 -переходов
-переходов может быть вычислен точно, т. к.
может быть вычислен точно, т. к.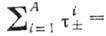
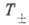 ,
где T-изотопич. спин нач. ядра.
,
где T-изотопич. спин нач. ядра.
При этом 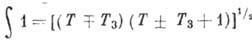 , где T3 - проекция изоспина для нач. ядра, численно равная
1/2 (Z-N)(предполагается, что b-переход
происходит между чистыми изосниновыми состояниями; учёт мезонных обменных токов
не меняет этого результата, что обусловлено сохранением изоспина). В случае
сверхразрешённых переходов
, где T3 - проекция изоспина для нач. ядра, численно равная
1/2 (Z-N)(предполагается, что b-переход
происходит между чистыми изосниновыми состояниями; учёт мезонных обменных токов
не меняет этого результата, что обусловлено сохранением изоспина). В случае
сверхразрешённых переходов  между соседними членами изомультиплета
между соседними членами изомультиплета
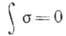 и, при T=1,
и, при T=1,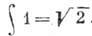 , Для таких сверхразрешённых переходов величины
, Для таких сверхразрешённых переходов величины 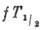
Табл. 1. - Характеристики некоторых
сверхразрешённых b- переходов
|
Переход |
|
Т1/2 |
|
|
|
n |
1/2 + |
11,7 + 0,3 мин |
782bl |
1187b35 |
|
3Н |
1/2 + |
3,87,108 С |
18,65b0,2 |
1132b40 |
|
6Не |
0+ |
0,813b0,7 с |
3500b2,0 |
808b32 |
|
17F |
5/2 +
|
66,0b0,5 с |
1748b6 |
2380b40 |
|
35Cl |
3/2 +
|
1,804b0,21 с |
4948b30 |
5680b400 |
|
14O |
0+ |
71,36b0,09 с |
1012, 6b1, 4 |
3066bl0 |
|
34С1 |
0+ |
1,565b0,007 С |
4460b4,5 |
3055b20 |
|
42Sc |
0+ |
0,6830b0,0015 с |
5409b2,3 |
3077b9 |
|
46V |
0+ |
0,4259b0,0008 с |
6032, 1b2, 2 |
3088b8 |
|
50Mn |
0+ |
0,2857b0,0006 с |
6609, 0b2, 6 |
3082b9 |
должны быть одинаковыми, что хорошо
согласуется с эксперим. данными (табл. 1). Соотношение (11) позволило определить
величину 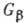 по измеренным
значениям
по измеренным
значениям 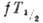 для
для
 переходов (с
учётом эл--магн. радиац. поправок):
переходов (с
учётом эл--магн. радиац. поправок): 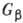 =(1,4057b0,0016b0,0070)*10-49
эрг*см3.
=(1,4057b0,0016b0,0070)*10-49
эрг*см3.
Гамов-теллеровские переходы  характеризуются единств. матричным элементом
характеризуются единств. матричным элементом 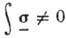 и
могут быть использованы для получения
информации о величине аксиально-векторной константы связи gA. Наиболее точное значение
и
могут быть использованы для получения
информации о величине аксиально-векторной константы связи gA. Наиболее точное значение 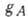 =-1,254b0,007
получено из данных по β‑распаду нейтрона.
=-1,254b0,007
получено из данных по β‑распаду нейтрона.
Затруднённые переходы отличаются от
сверхразрешённых относительно слабым перекрытием волновых функций начального и
конечного ядерных состояний, вследствие чего матричные элементы оказываются
малыми по сравнению с матричными элементами сверхразрешённых переходов. Примером
затруднённых переходов могут служить переходы  между состояниями, принадлежащими разным изоспиновым мультиплетам. Такие переходы
удовлетворяют правилам отбора фермиевского типа
между состояниями, принадлежащими разным изоспиновым мультиплетам. Такие переходы
удовлетворяют правилам отбора фермиевского типа 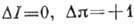 и описываются единств. матричным элементом
и описываются единств. матричным элементом 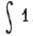 .
Если начальное и конечное ядерные
состояния являются чистыми изоспиновыми состояниями, принадлежащими разным изомультиплетам,
.
Если начальное и конечное ядерные
состояния являются чистыми изоспиновыми состояниями, принадлежащими разным изомультиплетам,
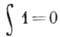 и вероятность
перехода W=0.
и вероятность
перехода W=0.
Однако кулоновское взаимодействие в
ядрах нарушает изотопич. инвариантность и приводит к тому, что ядерные состояния
(особенно в тяжёлых ядрах) не являются чистыми и содержат примеси состояний
с др. изоспином. Вследствие этого матричные элементы таких переходов отличны
от нуля, но они малы по сравнению с обычными разрешёнными матричными элементами,
хотя правила отбора по спину и чётности и удовлетворены.
Запрещённые переходы - переходы,
в к-рых лептонная пара уносит орбитальный момент и (или) осн. вклад в амплитуду
процесса дают малые матричные элементы от операторов 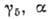 в эффективном гамильтониане
в эффективном гамильтониане 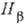 .
.
Запрещённые переходы классифицируют
по степени малости матричного элемента. К переходам 1-го порядка
запрета относятся переходы, описываемые матричными элементами
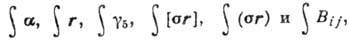
где
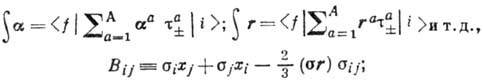
i, j = 1, 2, 3; xi-комцонента
вектора r. Первые 2 матричных элемента обусловлены векторным током, остальные
-аксиальным. Матричные элементы, содержащие величину r, возникают в том
случае, когда лептонная пара уносит орбитальный момент 1. Правила отбора
для матричных элементов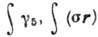 имеют вид:
имеют вид:
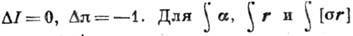 правила отбора:
правила отбора: 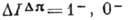 (переходы
(переходы  запрещены).
Переходы, описываемые матричным элементом
запрещены).
Переходы, описываемые матричным элементом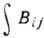 ,
наз. уникальными переходами первого запрета.
В таких переходах лентонная пара уносит полный момент 2, т. е. правила отбора
имеют вид:
,
наз. уникальными переходами первого запрета.
В таких переходах лентонная пара уносит полный момент 2, т. е. правила отбора
имеют вид:
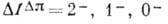 (запрещены переходы
(запрещены переходы 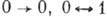 ,
, 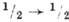 ). Матричные
элементы
). Матричные
элементы 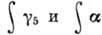 имеют
порядок малости
имеют
порядок малости 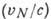 .
Для матричных элементов, содержащих величину r, естественно ожидать малости
порядка
.
Для матричных элементов, содержащих величину r, естественно ожидать малости
порядка 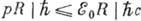 . Однако
это справедливо только для уникальных переходов. Для остальных матричных элементов
в случае, когда заряд ядра Z удовлетворяет условию
. Однако
это справедливо только для уникальных переходов. Для остальных матричных элементов
в случае, когда заряд ядра Z удовлетворяет условию 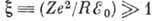 ,
кулоновские эффекты приводят к возрастанию волновой функции электрона внутри ядра,
вследствие чего эти матричные элементы имеют порядок малости Z/137, а не
,
кулоновские эффекты приводят к возрастанию волновой функции электрона внутри ядра,
вследствие чего эти матричные элементы имеют порядок малости Z/137, а не 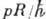 .
Условие
.
Условие 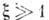 выполняется
для большинства
выполняется
для большинства 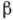 -переходов.
-переходов.
С ростом порядка запрета кол-во матричных
элементов, определяющих вероятность перехода, увеличивается и трудность анализа
эксперим. данных возрастает; при этом сами матричные элементы убывают по порядку
величины. Правила отбора при 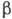 -переходах
п-го порядка запрета:
-переходах
п-го порядка запрета: 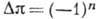 ,
, 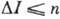 для обычных
переходов
для обычных
переходов 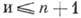 для
уникальных переходов.
для
уникальных переходов.
С ростом п и уменьшением матричных
элементов величина 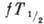 возрастает. Хотя диапазон её изменения уже, чем для
возрастает. Хотя диапазон её изменения уже, чем для 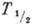 ,
он всё же очень велик; поэтому принято характеризовать
,
он всё же очень велик; поэтому принято характеризовать 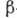 -переходы
величиной
-переходы
величиной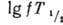 (табл.
2).
(табл.
2).
В сочетании с правилами отбора анализ
величин 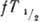 позволяет
определить неизвестные значения ядерных спинов и чётностей, т. е. является одним
из важных методов ядерной спектроскопии. T. к. величины
позволяет
определить неизвестные значения ядерных спинов и чётностей, т. е. является одним
из важных методов ядерной спектроскопии. T. к. величины 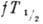 непосредственно связаны с матричными элементами
непосредственно связаны с матричными элементами 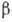 -переходов,
то они содержат информацию о ядерной структуре.
-переходов,
то они содержат информацию о ядерной структуре.
Табл. 2 -Правила отбора для  - переходов
различных типов
- переходов
различных типов

 -спектры
экспериментально исследуются, как правило, с помощью бета-спектрометров. В случае разрешённых переходов
-спектры
экспериментально исследуются, как правило, с помощью бета-спектрометров. В случае разрешённых переходов  -спектры
описываются выражением:
-спектры
описываются выражением:
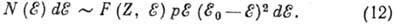
Для исследования 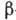 -спектров
удобно пользоваться т. н. графиками Кюри, к-рые изображают зависимость величины
-спектров
удобно пользоваться т. н. графиками Кюри, к-рые изображают зависимость величины
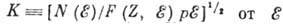 . Для разрешённых
переходов график Кюри имеет вид отрезка прямой, пересекающей ось абсцисс в точке
. Для разрешённых
переходов график Кюри имеет вид отрезка прямой, пересекающей ось абсцисс в точке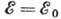 (рис. 4). Отличие перехода от разрешённого приводит к нарушению линейности.
Бета-спектры запрещённых переходов могут значительно отличаться от разрешённых
спектров из-за наличия зависящих от энергии членов в матричном элементе. Этот
эффект обычно учитывается введением в правую часть выражения (12) зависящего
от энергии множителя S
(рис. 4). Отличие перехода от разрешённого приводит к нарушению линейности.
Бета-спектры запрещённых переходов могут значительно отличаться от разрешённых
спектров из-за наличия зависящих от энергии членов в матричном элементе. Этот
эффект обычно учитывается введением в правую часть выражения (12) зависящего
от энергии множителя S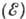 (т. н. спектрального формфактора).
Для уникальных переходов 1-го запрета (в пренебрежении кулоновскими эффектами):
(т. н. спектрального формфактора).
Для уникальных переходов 1-го запрета (в пренебрежении кулоновскими эффектами):
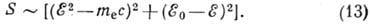
Уникальные переходы n-го запрета
часто характеризуют не величинами 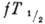 , а
, а 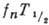 , где fn определяется ф-лой вида (9б ), в подынтегральное выражение
, где fn определяется ф-лой вида (9б ), в подынтегральное выражение
Рис. 4. Графики Кюри
 -спектров
нейтрона (а), трития (б) и 6Не (в).
-спектров
нейтрона (а), трития (б) и 6Не (в).
к-рой введён спектральный формфактор
Sn (табл. 2).
(табл. 2).
Энергетич. спектры обычных (не уникальных)
переходов 1-го запрета, как правило, близки к разрешённым. Матричные элементы
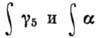 практически не
содержат зависимости от энергии лептонов; для матричных элементов
практически не
содержат зависимости от энергии лептонов; для матричных элементов 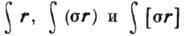 в случае
в случае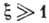 из-за кулоновских эффектов спектральный
формфактор не зависит от энергии. Исключение составляют нек-рые
из-за кулоновских эффектов спектральный
формфактор не зависит от энергии. Исключение составляют нек-рые 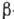 -переходы
1-го запрета, в к-рых главные, не зависящие от энергии члены в матричном элементе
взаимно сокращаются и малые поправки, зависящие от энергии, начинают играть
существ. роль.
-переходы
1-го запрета, в к-рых главные, не зависящие от энергии члены в матричном элементе
взаимно сокращаются и малые поправки, зависящие от энергии, начинают играть
существ. роль.
Такая ситуация реализуется, напр., в
случае β‑распада 210Bi (RaE, рис. 5). Во многих случаях бета-распада
происходит не в одно к--л. состояние дочернего ядра, а в два или неск. состояний; при этом экспериментально
наблюдаемый 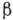 -спектр
складывается из двух или неск. парциальных спектров с разл. значениями граничных
энергий. Такие
-спектр
складывается из двух или неск. парциальных спектров с разл. значениями граничных
энергий. Такие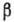 ,
спектры наз. сложными. Исследование
,
спектры наз. сложными. Исследование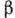 -спектров
вблизи
-спектров
вблизи 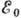 позволяет
получить информацию о
позволяет
получить информацию о 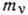 .
Если
.
Если 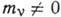 , то спектр
разрешённых переходов должен отличаться от (12) и даётся ф-лой:
, то спектр
разрешённых переходов должен отличаться от (12) и даётся ф-лой:
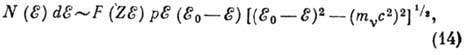
из к-рой следует, что форма спектра
вблизи 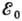 существенно зависит от
существенно зависит от 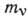 .
Отличие
.
Отличие 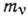 от 0
приводит к отклонению графика Кюри в области
от 0
приводит к отклонению графика Кюри в области 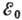 от линейного. Для определения
от линейного. Для определения 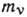 необходимо сравнить график Кюри с рассчитанными при разных значениях
необходимо сравнить график Кюри с рассчитанными при разных значениях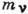 зависимостями
зависимостями 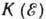 .
Исследования
.
Исследования  -спектра
3H (
-спектра
3H ( =18,61
кэВ) дали
=18,61
кэВ) дали  <
35 эВ/с2. Результаты, полу-
<
35 эВ/с2. Результаты, полу-
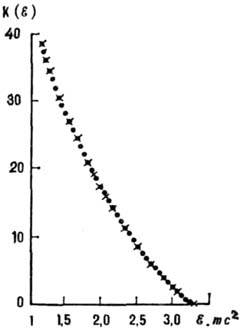
Рис. 5. График Кюри для β‑распада RaE.
ченные при изучении 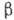 -спектра
3H: 14 эВ < mn
< 46 эВ, нуждаются в дальнейшем подтверждении.
-спектра
3H: 14 эВ < mn
< 46 эВ, нуждаются в дальнейшем подтверждении.
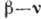 -угловые корреляции при бета-распаде. Для разрешённых переходов угловая корреляция определяется
соотношением:
-угловые корреляции при бета-распаде. Для разрешённых переходов угловая корреляция определяется
соотношением:
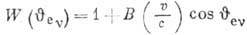 .
.
Для чисто фермиевских  или чисто гамов-теллеровских
или чисто гамов-теллеровских  переходов величина В зависит только от типа взаимодействия: в случае
переходов величина В зависит только от типа взаимодействия: в случае
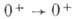 переходов В=+1
для V-варианта взаимодействия и B=-1 для S-взаимодействия; в случае
переходов В=+1
для V-варианта взаимодействия и B=-1 для S-взаимодействия; в случае 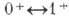 переходов
переходов 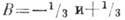 для
А- и Т-вариантов. В отличие от β‑распада нейтрона,
который не является ни чисто фермиевским, ни чисто гамов-теллеровским переходом
для
А- и Т-вариантов. В отличие от β‑распада нейтрона,
который не является ни чисто фермиевским, ни чисто гамов-теллеровским переходом
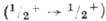 , бета-распад
ядер даёт возможность получить прямую информацию о типе слабого взаимодействия.
, бета-распад
ядер даёт возможность получить прямую информацию о типе слабого взаимодействия.
Исследования 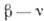 -корреляции сложны из-за невозможности регистрации нейтрино. Вместо них изучают
корреляции β‑частица - ядро отдачи. Обычно исследуется энергетич. спектр ядер отдачи, форма к-рого
зависит от В. Напр., для
-корреляции сложны из-за невозможности регистрации нейтрино. Вместо них изучают
корреляции β‑частица - ядро отдачи. Обычно исследуется энергетич. спектр ядер отдачи, форма к-рого
зависит от В. Напр., для 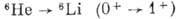 эксперим. значение В=-0,334b0,003, что позволило сделать вывод
о том, что гамов-теллеровские переходы обусловлены А-взаимодействием.
эксперим. значение В=-0,334b0,003, что позволило сделать вывод
о том, что гамов-теллеровские переходы обусловлены А-взаимодействием.
Величину В для фермиевских переходов
удалось определить в переходе  , для к-рого гамов-теллеровский матричный элемент мал:
, для к-рого гамов-теллеровский матричный элемент мал:
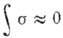 . Полученное значение В =
0,97 b0,14 означает, что
фермиевские переходы обусловлены V-взаимодействием. Исследования
. Полученное значение В =
0,97 b0,14 означает, что
фермиевские переходы обусловлены V-взаимодействием. Исследования  -корреляций и формы
-корреляций и формы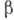 -спектров
в разрешённых переходах позволили получить ограничения на константы скалярного
и тензорного взаимодействий:
-спектров
в разрешённых переходах позволили получить ограничения на константы скалярного
и тензорного взаимодействий: 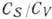 =-0,001b0,006;
=-0,001b0,006;
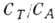 =-0,0004b0,0003.
=-0,0004b0,0003.

Дело в том, что в его постановке и выводах произведена подмена, аналогичная подмене в школьной шуточной задачке на сообразительность, в которой спрашивается:
- Cколько яблок на березе, если на одной ветке их 5, на другой ветке - 10 и так далее
При этом внимание учеников намеренно отвлекается от того основополагающего факта, что на березе яблоки не растут, в принципе.
В эксперименте Майкельсона ставится вопрос о движении эфира относительно покоящегося в лабораторной системе интерферометра. Однако, если мы ищем эфир, как базовую материю, из которой состоит всё вещество интерферометра, лаборатории, да и Земли в целом, то, естественно, эфир тоже будет неподвижен, так как земное вещество есть всего навсего определенным образом структурированный эфир, и никак не может двигаться относительно самого себя.
Удивительно, что этот цирковой трюк овладел на 120 лет умами физиков на полном серьезе, хотя его прототипы есть в сказках-небылицах всех народов всех времен, включая барона Мюнхаузена, вытащившего себя за волосы из болота, и призванных показать детям возможные жульничества и тем защитить их во взрослой жизни. Подробнее читайте в FAQ по эфирной физике.
|
|