GPSS World имеет все необходимые средства, которые позволяют провести:
Сущность этого эксперимента состоит в проведении многофакторного дисперсионного анализа с целью выявления степени влияния различных факторов и их комбинаций (взаимодействий) на значение целевой функции (функции отклика, представленной в виде уравнения регрессии).
Пример 1. В условиях примера 6.1 (прямая задача) требуется исследовать зависимость вероятности обработки запросов от трех факторов, например, при следующих их минимальных и максимальных значениях (табл. 1):
Для проведения дисперсионного анализа нужно воспользоваться созданным в п. 6.3.1 объектом "Модель". В программе модели удалите последние три строки:
START 1000,NP ; Прогоны до установившегося режима RESET ; Сброс накопленной статистики START 9604 ; Количество прогонов модели
Откройте модель Прямая задача. Выберите Edit / Insert Experiment / Screening … ( Правка / Вставить эксперимент / Отсеивающий … ).
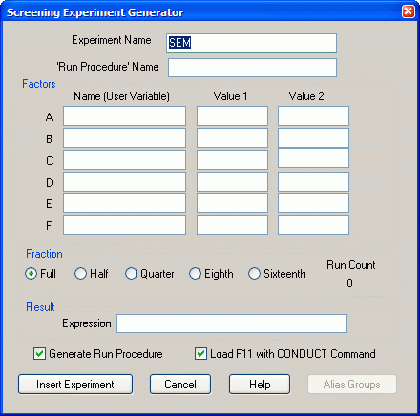
Откроется диалоговое окно Screening Experiment Generator ( Генератор отсеивающего эксперимента ) (рис. 1).
Приступите к заполнению полей диалогового окна.
В поля Experiment Name ( Имя эксперимента ) и Run Procedure Name ( Имя процедуры запуска ) введите, например, Dis_Server и Dis_Server_Run соответственно (рис. 2).
Имена эксперименту и процедуре запуска эксперимента дает пользователь.
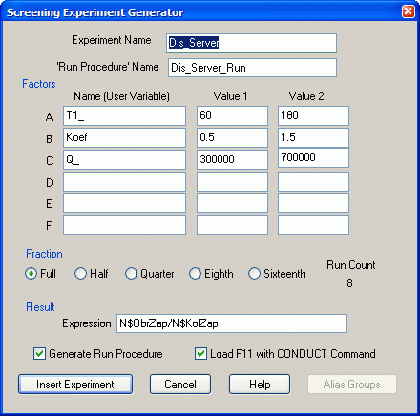
Дальше расположена группа полей Factors ( Факторы ). В рассматриваемом примере определяется вероятность обработки запросов, поступающих на сервер. Факторы, влияние которых необходимо исследовать, были определены нами ранее (см. табл. 1).
В GPSS World максимальное количество факторов, влияние которых на функцию отклика можно исследовать посредством дисперсионного анализа, равно шести.
Для каждого фактора необходимо выбрать два уровня - нижний и верхний. Рекомендуется выбирать уровни, значительно отстоящие друг от друга. Это необходимо для получения также значительно отличающихся откликов.
Введите ранее выбранные факторы, начиная с фактора А. В поле Name ( User Variable ) ( Имя ( Переменная пользователя )) введите имя фактора, в поля Value1 и Value2 - его нижний и верхний уровни соответственно. После ввода всех факторов для дальнейшей работы будем иметь факторы А, В и С.
Ниже идет группа Fraction ( Часть полного эксперимента ). Эксперимент, проводимый в GPSS World, может быть полным факторным экспериментом (ПФЭ) или дробным факторным экспериментом (ДФЭ). Группа Fraction ( Часть дробного эксперимента ) позволяет это задавать, т. е. позволяет провести стратегическое планирование эксперимента, цель которого, как вам известно, является определение количества наблюдений и сочетаний уровней факторов в них для получения наиболее полной и достоверной информации о поведении системы.
Установке ПФЭ соответствует кнопка Full, для ДФЭ в 1/2 от ПФЭ - Half, в 1/4 - Quarter, в 1/8 - Eight, в 1/16 - Sixteen.
Установите пока Half ( 1/2 ). Справа под Run Count появится число 4, так как 22 =4. Это количество наблюдений, которое необходимо сделать. Количество прогонов в каждом наблюдении будет указано позже.
В поле Expression ( Выражение ) группы Result ( Результат ) введите выражение, по которому вычисляется вероятность обработки запросов: N$ObrZap/N$KolZap.
После группы Result ( Результат ) расположены два флажка, позволяющие выбирать опции.
При выборе опции Generate Run Procedure вместе с экспериментом создается стандартная процедура запуска, которую пользователь может корректировать согласно своим требованиям.
Выбор второй опции Load F11 with CONDUCT Command закрепляет команду CONDUCT за функциональной клавишей F11. Тогда после создания объекта "Процесс моделирования" для запуска эксперимента нужно только нажать функциональную клавишу F11. Выберите обе опции.
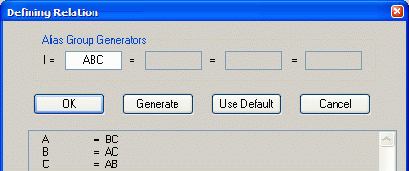
Перед созданием эксперимента необходимо изучить группы смешивания с целью осуществления стратегического планирования эксперимента. Для этого нужно нажать кнопку Alias Groups ( Группы смешивания ). Появится диалоговое окно Alias Groups ( Группы смешивания ) (рис. 3).
При изучении групп смешивания необходимо вначале найти отсутствующие факторы, а затем факторы, которые неразличимы, так как находятся в одной группе смешивания. Например, взаимодействие факторов А и В - АВ.
Из рис. 3 видно, что отсутствующих факторов нет. Факторы А, В и С находятся в различных группах смешивания по два фактора в каждом. Невозможно будет судить об эффектах, т. е. о влиянии на отклик взаимодействий двух факторов. В некоторых случаях этого будет достаточно.
Нажмите кнопку Cancel ( Отмена ).
В диалоговом окне Screening Experiment Generator ( Генератор отсеивающего эксперимента ) в группе Fraction ( Часть дробного эксперимента ) установите Full ( ПФЭ ). Под Run Count появится число 8.
Обратите внимание, что кнопка Alias Groups ( Группы смешивания ) при установке полного факторного эксперимента Full ( ПФЭ ) не будет активной.
Теперь необходимо создать Plus - операторы и вставить их в нижнюю часть модели Прямая задача. Для этого нажмите кнопку Insert Experiment ( Вставить эксперимент ), расположенную в левой нижней части диалогового окна Screening Experiment Generator ( Генератор отсеивающего эксперимента ).
Так как была выбрана опция Generate Run Procedure, то создана стандартная процедура запуска. Появится ее диалоговое окно, дающее возможность пользователю изменить процедуру запуска согласно своим требованиям.
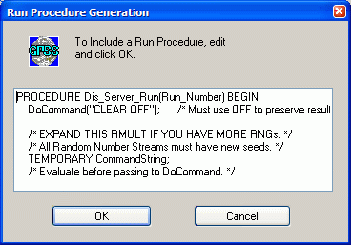
Введите через пробел после слова PROCEDURE указанное ранее имя процедуры Dis_Server_Run, оставив в скобках ( Run_Number ), без изменения (рис. 4).
Перейдите, пользуясь клавишами вверх-вниз, в конец процедуры запуска. Там в разделе Set up your own run conditions ( Задайте свои условия наблюдения ) имеются две команды START, между которыми находится команда RESET (рис. 5).
Поясним назначение этих команд.
Для получения достоверной статистики существуют три подхода (см. п. 4.9). В генераторе экспериментов использован третий подход.
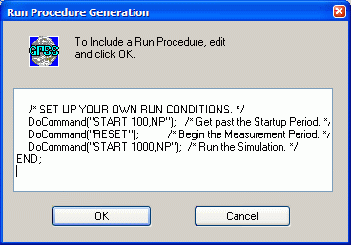
Первой командой START
DoCommand("START 100,NP"); /*Get past the Startup Period. */определяется количество прогонов в неустоявшемся режиме.
Подразумевается, что если моделирование выполняется долго, то система приходит в стационарное состояние. Сколько времени следует вести моделирование, чтобы достичь стационарного состояния? Часто ответ на этот вопрос можно получить из опыта экспериментирования с моделью. Команда RESET служит для этого. Она сбрасывает в ноль накопленную на неустоявшемся режиме статистику без удаления транзактов из процесса моделирования. Второй командой START
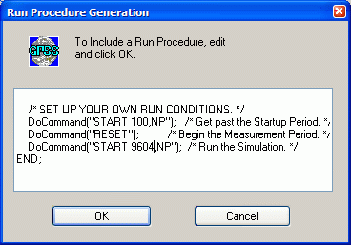
DoCommand("START 1000,NP"); /*Run the Simulation. */определяется количество прогонов в наблюдении, т. е. количество прогонов, которое было определено ранее при тактическом планировании эксперимента: N=9604. Измените 1000 на 9604 (рис. 6).
Корректировка процедуры запуска возможна до и после того, как она будет добавлена к объекту "Модель". После корректировки нажмите Ok. Сгенерированный Plus - эксперимент представлен ниже. Изучите его. Это необходимо для создания собственных экспериментов.
В начале автоматически сгенерированного эксперимента определяется и инициализируется в неопределенное состояние ( UNSPECIFIED ) матрица результатов. Далее имеются Plus - операторы, которые для каждого из наблюдений определяют сочетания уровней факторов. В рассматриваемом примере таких сочетаний восемь.
Plus - эксперимент содержит также вызов Plus - процедуры запуска. Процедура запуска осуществляет связь между генерируемым экспериментом и процессом моделирования. Она вызывается столько раз, сколько требуется сделать наблюдений. Так как процедура запуска вызывается Plus - экспериментом, ей разрешается вызывать библиотечную процедуру DoCommand и, следовательно, выполнять RMULT, CLEAR, RESET и многие другие команды GPSS. Поэтому все команды, необходимые для определения условий наблюдения, следует помещать в процедуру запуска.
Для сохранения матрицы результатов при обнулении переменных перед очередным наблюдением используется команда CLEAR OFF. Для изменения начального числа генератора случайных чисел в каждом наблюдении процедуре передается номер запуска.
****************************************************
* Dis_Server *
* Факторный отсеивающий эксперимент *
****************************************************
Dis_Server_Results MATRIX ,2,2,2
INITIAL Dis_Server_Results,UNSPECIFIED
Dis_Server_NextRunNumber EQU 0
EXPERIMENT Dis_Server() BEGIN
/* Наблюдение 1 */
T1_ = 60;
Koef = 0.5;
Q_ = 300000;
IF (StringCompare(DataType(Dis_Server_Results[1,1,1]),
"UNSPECIFIED")'E'0)
THEN BEGIN
/* Установить начальное значение переменной количества наблюдений */
Dis_Server_NextRunNumber = 1;
/* Записать данные наблюдения и запустить процесс моделирования*/
Dis_Server_GetResult();
Dis_Server_Results[1,1,1] = N$ObrZap/N$KolZap;
END;
/* Наблюдение 2 */
T1_ = 60;
Koef = 0.5;
Q_ = 700000;
IF (StringCompare(DataType(Dis_Server_Results[1,1,2]),
"UNSPECIFIED")'E'0)
THEN BEGIN
/* Записать данные наблюдения и запустить процесс моделирования */
Dis_Server_GetResult();
Dis_Server_Results[1,1,2] = N$ObrZap/N$KolZap;
END;
/* Наблюдения 3 - 7 для краткости пропущены */
/* Наблюдение 8 */
T1_ = 180;
Koef = 1.5;
Q_ = 700000;
IF (StringCompare(DataType(Dis_Server_Results[2,2,2]),
"UNSPECIFIED")'E'0)
THEN BEGIN
/* Записать данные наблюдения и запустить процесс моделирования */
Dis_Server_GetResult();
Dis_Server_Results[2,2,2] = N$ObrZap/N$KolZap;
END;
/* Эффекты смешивания в дробном факторном эксперименте */
SE_Effects(Dis_Server_Results,"I");
END;
*******************************************************
* Процедура запуска наблюдения *
*******************************************************
PROCEDURE Dis_Server_GetResult() BEGIN
/* Выполнить указанное число прогонов и записать результаты. */
/* Факторы для этого наблюдения уже были определены. */
TEMPORARY CurrentYield,ShowString,CommandString;
/* Вызов процедуры запуска */
Dis_Server_Run(Dis_Server_NextRunNumber);
CurrentYield = N$ObrZap/N$KolZap;
ShowString = PolyCatenate("Run ",String(Dis_Server_NextRunNumber),
". ", "" );
ShowString = PolyCatenate(ShowString," Yield=",String(CurrentYield),
". ");
ShowString = PolyCatenate(ShowString," T1_=",String(T1_), ";" );
ShowString = PolyCatenate(ShowString," Koef=",String(Koef), ";" );
ShowString = PolyCatenate(ShowString," Q_=",String(Q_), ";" );
CommandString = PolyCatenate("SHOW """,ShowString,
"""", "" );
DoCommand(CommandString);
Dis_Server_NextRunNumber = Dis_Server_NextRunNumber + 1;
RETURN CurrentYield;
END;
*******************************************************
* Процедура запуска *
*******************************************************
PROCEDURE Dis_Server_Run(Run_Number) BEGIN
DoCommand("CLEAR OFF"); /* Использовать OFF для сохранения результата. */
/* Увеличьте число команд RMULT, если у вас большее число ГСЧ. */
/* Задать новые случайные числа всем потокам случайных чисел. */
TEMPORARY CommandString;
/* Вычислить, прежде чем перейти к DoCommand. */
CommandString = Catenate("RMULT ",Run_Number#111);
/* DoCommand контролирует строку в глобальном контексте. */
DoCommand(CommandString);
/* Установить собственные условия наблюдения. */
DoCommand("START 100,NP"); /* Пройти неустоявшийся режим. */
DoCommand("RESET"); /* Начать период измерений. */
DoCommand("START 9604,NP"); /* Провести моделирование. */
END;Проведем эксперимент. Для вызова эксперимента предназначена команда CONDUCT. Однако за функциональной клавишей [F11] была закреплена соответствующая команда CONDUCT ( Edit / Settings / Function Keys ( Правка / Настройки / Функциональные клавиши ).
Проведите трансляцию, т. е. создайте объект "Процесс моделирования", для чего нажмите [Ctrl]+[Alt]+[S] или выполните команду Command / Create Simulation ( Команда / Создать процесс моделирования ).
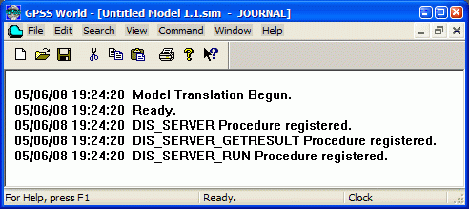
При отсутствии ошибок в сгенерированном эксперименте в окне Journal ( Журнал ) появится сообщение (рис. 7), свидетельствующее об отсутствии ошибок.
Теперь нажмите функциональную клавишу [F11]. Эксперимент начинает работать.
В ходе выполнения сгенерированного эксперимента автоматически создается отчет, который по готовности записывается в окно Journal ( Журнал ) объекта "Процесс моделирования". Фрагмент отчета для четырех наблюдений ( Run1 : Run4 ) показан на рис. 8. В отчете содержатся Yield - целевая функция и значения факторов, при которых получение значение целевой функции.
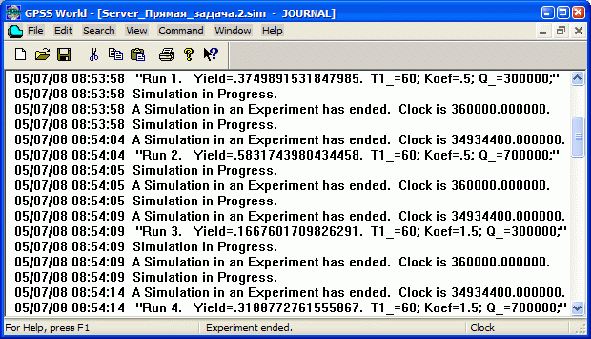
Так как эксперимент включает 8 наблюдений по 9604 прогонов в каждом из них, то будет выдано 8 отчетов (на рис. 8 в целях сокращения показаны только первые четыре отчета). Окончательные результаты моделирования после статистической обработки будут выведены в виде таблицы Anova (рис. 9).
В таблице каждый фактор и взаимодействие факторов представлены отдельной строкой. В каждой строке для всех эффектов указаны коэффициенты, с которыми они входят в целевую функцию (столбец Effect ), а для главных эффектов (А, В, С) - суммы квадратов отклонений, аналогичных величинам Q 1 (см. п. 5.7) - столбец Sum of Squares.
В столбце Degrees of Freedom приведены степени свободы соответствующих измерений.
В столбце F-for Only Main Effects - вычисленные значения F-статистик для главных эффектов, а в столбце Critical Value of F (p=0,5) - соответствующие критические значения F - распределения для уровня значимости 50%.
В строке Error показаны остаточная составляющая дисперсии (аналогичная Q 2 в п. 5.7) и соответствующая степень свободы.
В строке Total - общая сумма квадратов ошибок по всему эксперименту.
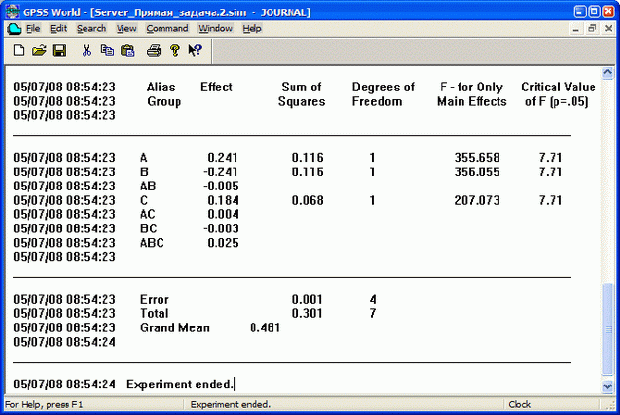
В строке Greand - среднее значение результата исследования (в примере - вероятности) по данным всего эксперимента.
Чем больше значение F-статистики ( F-for Only Main Effects ), тем сильнее эффект. Эффект, а, следовательно, и фактор, считается значимым, если превышает критическое значение ( Critical Value of F ( p=.05 )).
В данном примере факторы А, В и С являются значимыми, так как их F-статистики больше критического значения, равного 71.
Наибольший эффект на вероятность обработки запросов оказывают факторы В и А, так как они имеют самые большие и близкие статистики (356,055 и 355.658 соответственно). Обратите внимание, что эффекты факторов А и В противоположны.
Таким образом, по результатам моделирования можно сделать вывод, что при данном потоке и характеристике сервера вероятность обработки запросов в среднем составляет 0,481, т. е. вероятность потерь запросов составляет 0,519. Для уменьшения потерь запросов нужно продолжить исследование каждого значимого фактора и в первую очередь факторов В и А, как наиболее существенных.
Дисперсионный анализ (отсеивающий эксперимент) показывает силу влияния каждого фактора на наблюдаемую переменную (отклик). Однако оптимизация и количественный прогноз поведения систем часто являются основными задачами моделирования. В GPSS World решение таких задач возможно посредством проведения регрессионного анализа (оптимизирующего эксперимента).
Оптимизация моделируемого процесса состоит в определении таких значения уровней факторов, при которых показатель эффективности процесса достигает максимального значения (или минимального - в зависимости от смысла показателя эффективности).
В общем случае показатель эффективности представляется уравнением регрессии
где 
- значения уровней факторов процесса; 
-количество управляемых факторов.
Оптимизация многофакторного, особенно нелинейного уравнения регрессии, задача не простая, и для ее решения разработан ряд численных методов. Наиболее эффективен при компьютерном моделировании так называемый метод поверхностей, при котором уравнение регрессии трактуется как уравнение поверхности в многофакторном пространстве. Оптимальное решение в этом случае составляют координаты из значений факторов вершины (или впадины) этой поверхности. Поиск оптимума осуществляется последовательными изменениями (шагами) значений уровней факторов в направлении, на котором обнаруживается улучшение показателя эффективности. Такой метод реализован в GPSS World.
Пользователь задает исходные условия, а GPSS World автоматически создает план и проводит с поверхностью отклика эксперимент, который отыскивает оптимальное значение. В ходе эксперимента GPSS World пытается подобрать либо линейную модель, либо модель второго порядка (включая двухфакторные взаимодействия).
Рассмотрим на примере проведение регрессионного анализа (оптимизирующего эксперимента).
Пример 2. В условиях примера 6.1 провести регрессионный анализ результатов моделирования. При этом вычислительную сложность обработки запросов сервером взять распределенной не по нормальному, а по экспоненциальному закону, т. е. в программе модели примера 6.1 удалить строку
S2_ EQU 200000 ; Стандартное отклонение вычислительной сложности запросов, оп
а строку с блоком ADVANCE заменить строкой:
ADVANCE ((Exponential(32,0,S_))/Q_) ; Имитация обработки запроса
Откройте модель примера 6.1. Сохраните как Reg_Server. Внесите рекомендованные изменения.
Выберите Edit / Insert Experiment / Optimising : ( Правка / вставить эксперимент / Оптимизирующий : ). Откроется диалоговое окно Optimizing Experiment Generator ( Генератор оптимизирующего эксперимента ).
Введите имена факторов и значения уровней (рис. 10).
В поле Expression ( Выражение ) группы Result ( Результат ) введите выражение, по которому рассчитывается результат наблюдения:
(N$ObrZap/N$KolZap)
Оптимизирующий эксперимент нужно ограничить пределами. Группа полей Movement ( Пределы перемещения ) позволяет ограничить перемещение локальной экспериментальной области. Если это возможно, необходимо ввести пределы изменения для каждого фактора эксперимента. Другой способ ограничить поиск - задание величины Redirection Limit ( Предел изменения направления ). Это значение устанавливает предел на количество изменений направления движения эксперимента по факторному пространству.
Введите в поля эти данные, приведенные на рис. 10.
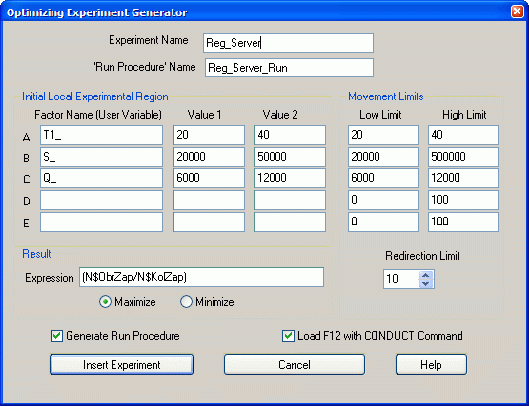
Далее, так как вероятность обработки запросов должна быть максимальной, оставьте Maximize. Также установите флажки, позволяющие выбрать опции Generate Run Procedure и Load F12 with CONDUCT Command. Назначение этих опций такое же, как и в генераторе отсеивающего эксперимента. Только после создания объекта "Процесс моделирования" для запуска эксперимента нужно нажать функциональную клавишу [ F12 ], а не [ F11 ].
Все необходимые данные введены в соответствующие поля. Нажмите кнопку Insert Experiment ( Вставить эксперимент ). Так как GPSS World было указано сгенерировать процедуру запуска, то появится диалоговое окно, позволяющее отредактировать ее так же, как и в генераторе отсеивающего эксперимента. После корректировки нажмите Ok. Автоматически сгенерированные Plus-операторы появятся в нижней части модели.
Для запуска эксперимента сначала создайте, нажав [ Ctrl ]+[ Alt ]+[ S ], объект "Процесс моделирования". При успешном завершении появится соответствующее сообщение (рис. 11).
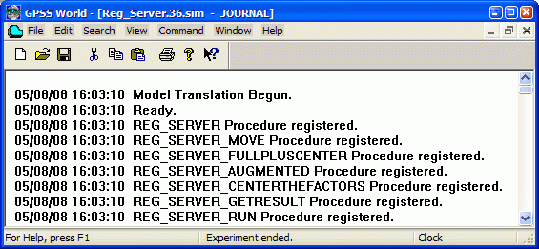
После такого сообщения нажмите функциональную клавишу [ F12 ]. Эксперимент начнет выполняться. В окно Journal ( Журнал ) процесса моделирования будут выводиться отчеты о состоянии и результатах каждого наблюдения.
По отчетам можно узнать о перемещении локальной экспериментальной области. Plus-эксперимент пытается переместить локальную экспериментальную область так, чтобы она включала в себя оптимальные условия. Если это происходит, или, если достигнут предел изменения направления или предел перемещения, эксперимент заканчивается.
Когда перемещение останавливается, в окно Journal ( Журнал ) также выводятся результаты проверки критерия адекватности и уравнение подобранной (найденной) поверхности отклика. Затем, если это еще не сделано, Plus-эксперимент пытается проверить прогнозируемые оптимальные условия, запустив процесс моделирования для них.
Результаты регрессионного анализа (оптимизирующего эксперимента), после 209 наблюдений, приведены на рис. 12.
Заметим, что это на 201 наблюдение больше, чем при проведении дисперсионного анализа (отсеивающего эксперимента) (п. 1). Оптимум не находится в локальной экспериментальной области.
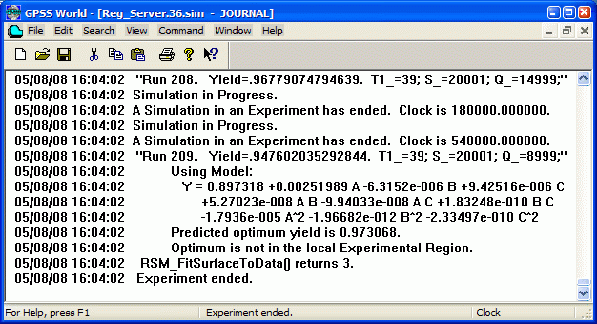
Полученное уравнение поверхности отклика имеет вид:
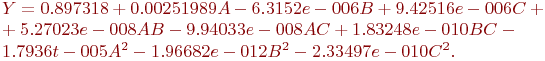
Оптимальное значение вероятности обработки запросов сервером составляет 0.973068.
При проведении оптимизирующего эксперимента важным является задание локальной экспериментальной области. Значения факторов, указанные исследователем, формируют начальную точку эксперимента. От этого зависит достижение его цели, заключающейся:
Следует иметь в виду, что цель получения математической модели в оптимизирующем эксперименте достигается не всегда.
Изготовление в цехе детали начинается через случайное время 
Выполнению операций предшествует подготовка. Длительность подготовки зависит от качества заготовки, из которой будет сделана деталь. Всего различных видов заготовок 
Время подготовки подчинено экспоненциальному закону. Частота появления различных заготовок и средние значения времени их подготовки заданы
табл. 2 дискретного распределения:
| Частота | 0,05 | 0,13 | 0,16 | 0,22 | 0,29 | 0,15 |
|---|---|---|---|---|---|---|
| Среднее время | 10 | 14 | 21 | 22 | 28 | 25 |
Для изготовления детали последовательно выполняются 
операций, продолжительностями 
соответственно. После каждой операции в течение времени 
следует контроль. Время выполнения операций и контроля - случайное. Контроль не проходят 
деталей соответственно.
Забракованные детали поступают на пункт окончательного контроля и проходят на нем проверку в течение случайного времени 
. В результате из общего количества не прошедших контроль деталей 
идут в брак, а оставшиеся 
деталей подлежат повторному выполнению операций, после которых они не прошли контроль. Если деталь во второй раз не проходит контроль, она окончательно бракуется.
Разработать имитационную модель процесса изготовления в цехе деталей.
Вариант 1. Исследовать влияние качества выполнения операций 
на время изготовления 
деталей (табл. 3). Результаты моделирования необходимо получить с точностью 
мин и доверительной вероятностью 
.
| Уровни факторов | Факторы | |||
|---|---|---|---|---|
 |  |  |  | |
| Нижний | 0,1 | 0,15 | 0,1 | 0,2 |
| Верхний | 0,25 | 0,35 | 0,2 | 0,9 |
Вариант 2. Исследовать влияние интервалов времени 
поступления заготовок и времени 
выполнения операций 1, 2, 3 соответственно на время подготовки 
деталей (табл. 4). Результаты моделирования также необходимо получить с точностью 
мин и доверительной вероятностью .
| Уровни факторов | Факторы | |||
|---|---|---|---|---|
| |  |  |  | |
| Нижний | 25 | 15 | 10 | 1 |
| Верхний | 45 | 45 | 35 | 2 |
Модель должна также позволять определять относительное количество готовых и забракованных деталей, среднее время изготовления одной детали. Сделать выводы о загруженности пунктов выполнения операций и необходимых мерах по сокращению времени изготовления деталей.
Процесс изготовления в цехе деталей представляет собой процесс, протекающий в многофазной разомкнутой системе массового обслуживания с ожиданием (рис. 13).
Представим, что подготовка заготовки и операции 1, 2 и 3 производятся на станках - ОКУ 1, 2, 3 и 4 соответственно. Пункт окончательного контроля можно также представить ОКУ. Необходимые для их имитации средства GPSS приведены на рис. 13.
Время подготовки заготовки и время выполнения операций даны в мин. Возьмем 1 ед. мод. вр. = 1мин. Для расчета количества прогонов модели примем, что среднее квадратическое отклонение времени изготовления 
деталей 
. Тогда
Программа модели обратной задачи приведена ниже.
; Модель изготовления деталей. Обратная задача ; Задание исходных данных Tn_ EQU 35 ; Среднее время между поступлениями заготовок T1 EQU 30 ; Среднее время выполнения 1-й операции, мин T2 EQU 25 ; Среднее время выполнения 2-й операции, мин T3 EQU 35 ; Среднее время выполнения 3-й операции, мин To3 EQU 6 ; Среднеквадратическое отклонение времени выполнения 3-й операции, мин Tk1 EQU 4 ; Среднее время контроля после 1-й операции, мин Tk2 EQU 5 ; Среднее время контроля после 2-й операции, мин Tk3 EQU 15 ; Среднее время контроля после 3-й операции, мин Tok3 EQU 2 ; Среднеквадратическое отклонение времени контроля после 3-й операции, мин Tk EQU 8 ; Среднее время окончательного контроля, мин q1_ EQU .12 ; Доля брака после 1-й операции q2_ EQU .15 ; Доля брака после 2-й операции q3_ EQU .10 ; Доля брака после 3-й операции q4_ EQU .80 ; Доля окончательного брака Det EQU 4 ; Количество деталей, которые нужно изготовить ; Описание функции времени подготовки заготовок для детали Pod FUNCTION RN10,D6 .05,10/.18,14/.34,21/.56,22/.85,28/1,25 ; Сегмент имитации изготовления деталей GENERATE (Exponential(1,0,Tn_)) ; Источник заготовок ; Подготовка заготовок для деталей QUEUE Pod ; Встать в очередь SEIZE Pod ; Начать подготовку заготовки DEPART Pod ; Покинуть очередь ADVANCE (Exponential(34,0,FN$Pod)) ; Имитация подготовки RELEASE Pod ; Закончить подготовку заготовки ; Имитация выполнения 1-й операции DCount ASSIGN 1,1 ; Код 1 в Р1-деталь проходит первый раз ASSIGN 2,1 ; Код 1 в Р2-признак 1-й операции Oper1 QUEUE P2 ; Встать в очередь SEIZE Konveer1 ; Начать первую операцию DEPART P2 ; Покинуть очередь ADVANCE (Exponential(23,0,T1)) ; Имитация 1-й операции RELEASE Konveer1 ; Закончить 1-ю операцию ADVANCE (Exponential(23,0,Tk1)) ; Контроль 1-й операции TRANSFER q1_,,Sboi ; Отправить брак на пункт контроля ; Имитация выполнения 2-й операции ASSIGN 2,2 ; Код 2 в Р2-признак 2-й операции Oper2 QUEUE P2 ; Встать в очередь SEIZE Konveer2 ; Начать вторую операцию DEPART P2 ; Покинуть очередь ADVANCE (Exponential(23,0,T2)) ; Имитация 2-й операции RELEASE Konveer2 ; Закончить 2-ю операцию ADVANCE (Exponential(23,0,Tk2)) ; Контроль 2-й операции TRANSFER q2_,,Sboi ; Отправить брак на пункт контроля ; Имитация выполнения 3-й операции ASSIGN 2,3 ; Код 3 в Р2-признак 3-й операции Oper3 QUEUE P2 ; Встать в очередь SEIZE Konveer3 ; Начать третью операцию DEPART P2 ; Покинуть очередь ADVANCE (Normal(20,(T3#K1),(To3#K1))) ; Имитация 3-й операции RELEASE Konveer3 ; Закончить 3-ю операцию ADVANCE (Normal(20,Tk3,Tok3)) ; Контроль 3-й операции TRANSFER q3_,,Sboi ; Отправить брак на пункт контроля TRANSFER ,Met2 ; Готовые детали ; Сегмент имитации работы пункта контроля Sboi QUEUE Kont ; Встать в очередь на пункт контроля SEIZE Kontr ; Занять пункт контроля DEPART Kont ; Покинуть очередь на пункт контроля ADVANCE (Exponential(23,0,Tk)) ; Окончательный контроль RELEASE Kontr ; Освободить пункт контроля TRANSFER q4_,,EndOper ; Отправить в окончательный брак TEST E P1,1,EndOper; Если второй раз, то в окончательный брак ASSIGN 1,2 ; Код 2 в Р1-деталь проходит второй раз Met1 TRANSFER ,(Met1+P2) TRANSFER ,Oper1 ; На повторное выполнение 1-й операции TRANSFER ,Oper2 ; На повторное выполнение 2-й операции TRANSFER ,Oper3 ; На повторное выполнение 3-й операции EndOper TERMINATE ; Счет брака ; Сегмент завершения моделирования и расчета результатов Met2 TEST L X$Prog,TG1,Met3 ; Если условие выполняется, то SAVEVALUE Prog,TG1 ; X$Prog=TG1 счетчику завершений SAVEVALUE NDet,0 ; Обнуление X$NDet Met3 SAVEVALUE NDet+,1 ; Счет количества готовых деталей TEST E X$NDet,Det,Ter1 ; Если готово Det деталей, зафиксировать один прогон TEST E TG1,1,Met4 ; Если содержимое счетчика завершений равно 1, то расчет результатов моделирования SAVEVALUE Brak,(INT(N$EndOper/X$Prog)) ; Количество забракованных деталей, шт. SAVEVALUE DoljaBrak,(X$Brak/(X$Brak+Det)) ; Общая доля брака SAVEVALUE DoljaDet,(Det/(X$Brak+Det)) ; Доля готовых деталей SAVEVALUE AC3,(AC1-X$AC2) SAVEVALUE TDet,((X$AC3/X$Prog)/60) ; Среднее время изготовления Det деталей, час SAVEVALUE SDet,((X$TDet/N_)#60) ; Среднее время изготовления одной детали, мин SAVEVALUE AC2,AC1 SAVEVALUE X$Prog,0 Met4 SAVEVALUE NDet,0 ; Обнуление X$NDet TERMINATE 1 ; Вычитание из счетчика завершений 1 Ter1 TERMINATE ; Вывод вспомогательных транзактов
Программа модели имеет достаточно подробный комментарий. Поэтому остановимся только на особенностях сегмента завершения моделирования и расчета результатов.
Поскольку результатом моделирования является оценка математического ожидания времени TDet изготовления Det деталей, то в ее вычислении используется абсолютное модельное время АС1 (системный числовой атрибут). При проведении дисперсионного анализа встроенный генератор эксперимента имеет две команды START, а между ними - команда RESET. Команда RESET не влияет на абсолютное модельное время. Поэтому АС1 будет суммой абсолютного модельного времени предварительных прогонов до установившегося режима, обозначим его АС2, и абсолютного модельного времени, пусть АС3, основных прогонов, в ходе которых собирается интересующая нас статистика. Нам для расчетов нужно АС3. Для его получения в программу введены строки:
SAVEVALUE AC3,(AC1-X$AC2) SAVEVALUE AC2,AC1
После предварительных прогонов в ячейке X$Prog сохранится указанное в первой команде START количество прогонов. Эта ячейка используется в первой строке рассматриваемого сегмента и ее содержимое должно быть равным нулю. В противном случае модель будет работать неверно. Для предотвращения ошибки введена строка:
SAVEVALUE X$Prog,0
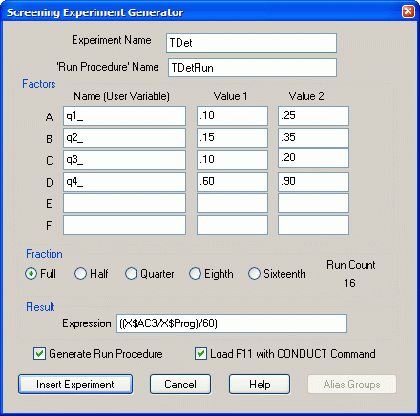
Вначале проведите эксперимент согласно варианту 1 (см. п. 3.3 и рис. 14).
Ранее (п. 4.9) отмечалось, что из трех подходов получения достоверной статистики наиболее удобен подход сброса статистики на определенном этапе моделирования с последующим его продолжением без модификации модели. Для реализации этого подхода в GPSS World имеется команда RESET.
Однако остается открытым вопрос: сколько нужно выполнить предварительных прогонов модели до сброса статистики?
Для получения ответа на этот вопрос проведите несколько экспериментов с моделью, меняя в каждом из них только количество предварительных прогонов модели.
В первой команде START генератора экспериментов укажите 20 прогонов. Во второй команде START - 170 прогонов, которые были определены ранее (п. 3.4). Результаты экспериментов - оценку матожидания времени TDet изготовления Det деталей - заносите в табл. 5.
| Оценка | Количество прогонов модели | ||||||
|---|---|---|---|---|---|---|---|
| 20 | 40 | 60 | 80 | 100 | 120 | 150 | |
| TDet | 3,988 | 3,975 | 4,007 | 4,024 | 3,986 | 3,995 | 4,044 |
Согласно табл. 5 изменяйте и количество прогонов модели. Для сокращения времени проведения экспериментов изменяйте их непосредственно в процедуре запуска генератора экспериментов.
По окончании экспериментов получите (табл. 5). Видно, что изменения результата моделирования столь малы, что ими для данной модели практически можно пренебречь.
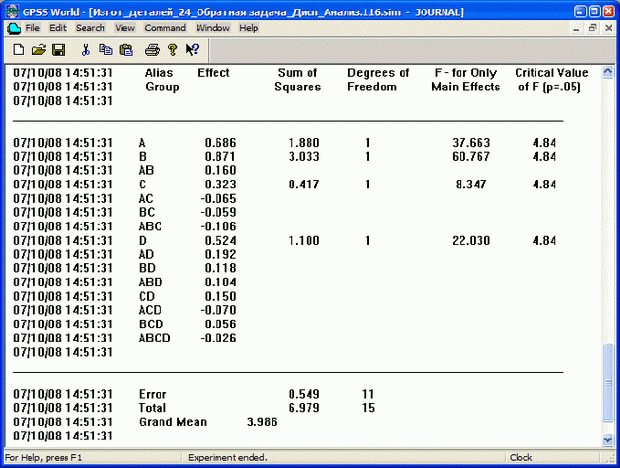
Повторите эксперимент, указав, например, 100 предварительных прогонов. Получите результаты дисперсионного анализа, представленные на рис. 15.
Видно, что все четыре фактора существенные. Наибольшее влияние на функцию отклика оказывает фактор В, что вполне логично, так как из первых трех имеет наибольший верхний уровень, т. е. наибольшую долю брака. Ожидаемое время изготовления четырех деталей DET = 4 деталей составляет ТDet = 3,986 ч.
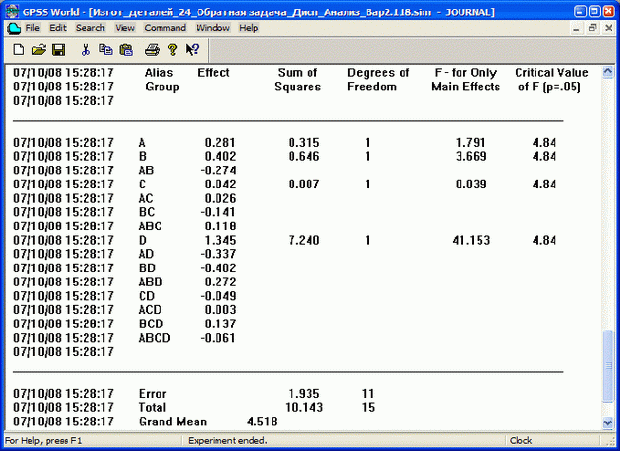
Теперь проведите эксперимент согласно варианту 2 (см. п. 3.3) при том же количестве предварительных и основных прогонов. Получите (рис. 16), что ожидаемое время изготовления четырех деталей ТDet = 4,518 ч. Все факторы, кроме фактора D (время выполнения третьей операции), несущественные.
Уменьшите верхний уровень фактора D: возьмем, например, K1 = 1,5. Проведите эксперимент с новым значением фактора D. Получите, что время изготовления ТDet ожидается 3,992 ч, а все факторы можно считать практически не существенными.
GENERATE TMod ; Время моделирования TEST L X$Prog,TG1,Met11 ; Если условие выполняется, то SAVEVALUE Prog,TG1 ; X$Prog=TG1 содержимому счетчика завершений SAVEVALUE Prog1,TG1 ; X$Prog1=TG1 содержимому счетчика завершений Met11 TEST E TG1,1,Met12 ; Если содержимое счетчика завершений равно 1, то расчет результатов моделирования SAVEVALUE NDet,(INT(N$EndOper1/X$Prog1)) ; Количество готовых деталей, шт. SAVEVALUE Brak,(INT(N$EndOper/X$Prog1)) ; Количество забракованных деталей, шт. SAVEVALUE DoljaBrak,(X$Brak/(X$Brak+X$NDet)) ; Общая доля брака SAVEVALUE DoljaDet,(X$NDet/(X$Brak+X$NDet)) ; Доля готовых деталей SAVEVALUE TDet,((AC1-X$AC2)/N$EndOper1) ; Среднее время изготовления одной детали, мин SAVEVALUE AC2,AC1 SAVEVALUE Prog,0 Met12 TERMINATE 1
Остальную необходимую корректировку модели выполните самостоятельно.
Боев В.Д., Сыпченко Р.П. Компьютерное моделирование
|
|
 |
