).Создание модели - акт необходимый при анализе и синтезе сложных систем, но далеко не конечный. Модель - не цель исследователя, а только инструмент для проведения исследований, инструмент эксперимента. В первых темах мы достаточно полно раскрыли афоризм: "Модель есть объект и средство эксперимента".
Эксперимент должен быть информативен, то есть давать всю нужную информацию, которой следует быть полной, точной, достоверной. Но она должна быть получена приемлемым способом. Это означает, что способ должен удовлетворять экономическим, временным и, возможно, другим ограничениям. Такое противоречие разрешается с помощью рационального (оптимального) планирования эксперимента.
Теория планирования эксперимента сложилась в шестидесятые годы двадцатого века благодаря работам выдающегося английского математика, биолога, статистика Рональда Айлмера Фишера (1890-1962 гг.). Одно из первых отечественных изданий: Федоров В. В. Теория оптимального эксперимента. 1971 г. Несколько позже сложилась теория и практика планирования имитационных экспериментов, элементы которых рассматриваются в настоящей теме.
Итак, как мы уже знаем, модель создается для проведения на ней экспериментов. Будем считать, что эксперимент состоит из наблюдений, а каждое наблюдение - из прогонов ( реализаций ) модели.
Для организации экспериментов наиболее важно следующее.
).Компьютерный эксперимент с имитационной моделью обладает преимуществами перед натурным экспериментом по всем этим позициям.
Что же такое компьютерный (машинный) эксперимент?
Компьютерный эксперимент представляет собой процесс использования модели с целью получения и анализа интересующей исследователя информации о свойствах моделируемой системы.
Эксперимент требует затрат труда и времени и, следовательно, финансовых затрат. Чем больше мы хотим получить информации от эксперимента, тем он дороже.
Средством достижения приемлемого компромисса между максимумом информации и минимумом затрат ресурсов является план эксперимента.
План эксперимента определяет:
Планирование экспериментов имеет следующие цели:
Таким образом, план эксперимента на компьютере представляет собой метод получения с помощью эксперимента необходимой информации.
Конечно, можно проводить исследования и по такому плану: исследовать модель во всех возможных режимах, при всех возможных сочетаниях внешних и внутренних параметров, повторять каждый эксперимент десятки тысяч раз - чем больше, тем точнее!
Очевидно, пользы от такой организации эксперимента мало, полученные данные трудно обозреть и проанализировать. Кроме того, большими будут затраты ресурсов, а они всегда ограничены.
Весь комплекс действий по планированию эксперимента разделяют на две самостоятельные функциональные части:
Стратегическое планирование - разработка условий проведения эксперимента, определение режимов, обеспечивающих наибольшую информативность эксперимента.
Тактическое планирование обеспечивает достижение заданных точности и достоверности результатов.
Формирование стратегического плана выполняется в так называемом факторном пространстве. Факторное пространство - это множество внешних и внутренних параметров, значения которых исследователь может контролировать в ходе подготовки и проведения эксперимента.
Объектами стратегического планирования являются:
Математические методы планирования экспериментов основаны на так называемом кибернетическом представлении процесса проведения эксперимента (рис. 4.1).
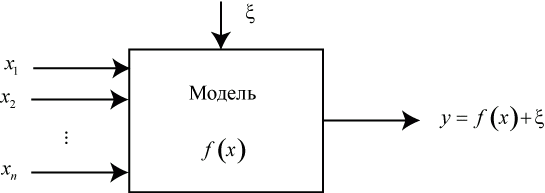
На рис. 4.1:
- входные переменные, факторы;
- выходная переменная (реакция, отклик);
- ошибка, помеха, вызываемая наличием случайных
факторов;
- оператор, моделирующий действие реальной системы,
определяющий зависимость выходной переменной 
от факторов 
Иначе: - модель процесса, протекающего в системе.
Первой проблемой, решаемой при стратегическом планировании, является выбор отклика (реакции), то есть определение, какие величины нужно измерять во время эксперимента, чтобы получить искомые ответы. Естественно, выбор отклика зависит от цели исследования.
Например, при моделировании информационно-поисковой
системы может интересовать исследователя время ответа системы на
запрос. Но может интересовать такой показатель как максимальное
число обслуженных запросов за интервал времени. А может, то и
другое. Измеряемых откликов может быть много: 
В дальнейшем будем говорить об одном отклике 
Второй проблемой стратегического планирования является выбор (определение) существенных факторов и их сочетаний, влияющих на работу моделируемого объекта. Факторами могут быть питающие напряжения, температура, влажность, ритмичность поставок комплектующих и многое другое. Обычно число факторов велико и чем меньше мы знакомы с моделируемой системой, тем большее, нам кажется, число их влияет на работу системы. В теории систем приводится так называемый принцип Парето:
это достигается достаточно глубоким изучением моделируемого объекта и протекающих в нем процессов.
Факторы могут быть количественными и (или) качественными.
Количественные факторы - это те, значения которых числа. Например, интенсивности входных потоков и потоков обслуживания, емкость буфера, число каналов в СМО, доля брака при изготовлении деталей и др.
Качественные факторы - дисциплины обслуживания (LIFO, FIFO и др.) в СМО, "белая сборка", "желтая сборка" радиоэлектронной аппаратуры, квалификация персонала и т. п.
Фактор должен быть управляемым. Управляемость фактора - это возможность установки и поддержания значения фактора постоянным или изменяющимся в соответствии с планом эксперимента. Возможны и неуправляемые факторы, например, влияние внешней среды.
К совокупности воздействующих факторов предъявляются два основных требования:
Совместимость факторов означает, что все комбинации значений факторов осуществимы.
Независимость факторов определяет возможность установления значения фактора на любом уровне независимо от уровней других факторов.
В стратегических планах факторы обозначают латинской
буквой 
, где индекс 
указывает номер (тип) фактора. Встречаются и такие
обозначения факторов: 
и т. д.
Третьей проблемой стратегического планирования является выбор значений каждого фактора, называемых уровнями фактора.
Число уровней может быть два, три и более. Например, если в качестве одного из факторов выступает температура, то уровнями могут быть: 80o С, 100o С, 120o С.
Для удобства и, следовательно, удешевления эксперимента число уровней следует выбирать поменьше, но достаточное для удовлетворения точности и достоверности эксперимента. Минимальное число уровней - два.
С точки зрения удобства планирования эксперимента целесообразно устанавливать одинаковое число уровней у всех факторов. Такое планирование называют симметричным.
Анализ данных эксперимента существенно упрощается, если назначить уровни факторов, равноотстоящие друг от друга. Такой план называется ортогональным. Ортогональность плана обычно достигают так: две крайние точки области изменения фактора выбирают как два уровня, а остальные уровни располагают так, чтобы они делили полученный отрезок на две части.
Например, диапазон питающего напряжения 30…50 В на пять уровней будет разбит так: 30 В, 35 В, 40 В, 45 В, 50 В.
Эксперимент, в котором реализуются все сочетания уровней всех факторов, называется полным факторным экспериментом (ПФЭ).
План ПФЭ предельно информативен, но он может потребовать неприемлемых затрат ресурсов.
Если отвлечься от компьютерной реализации плана
эксперимента, то число измерений откликов (реакций) модели 
при ПФЭ равно:
где 
- число уровней 
-го фактора, 
; 
- число факторов эксперимента.
Величина определяет структуру стратегического плана, то есть
количество наблюдений (информационных точек).
При машинной реализации ПФЭ в каждом наблюдении (информационной точке) нужно выполнить определенное число прогонов (реализаций) модели, чтобы обеспечить заданную точность и достоверность значений откликов. Определение числа прогонов модели является предметом тактического планирования.
Обозначим число прогонов в каждом наблюдении 
. Тогда для симметричного ПФЭ общее число 
необходимых прогонов модели равно:
Пример 4.1. Планируется провести компьютерный эксперимент, в котором на отклик модели влияют три фактора. Для каждого фактора установлены три уровня. Требования по точности и достоверности требуют 6000 прогонов модели на каждом уровне (для каждого наблюдения). Время одного прогона модели равно 2 с.
Оценить затраты времени на проведение компьютерного эксперимента.
Решение
Исходные данные: 
, 
, 
, 
.
Число прогонов модели: 
.
Затраты времени : 
.
Ранее на рис. 4.1 был
показан оператор преобразования - математическая модель процесса
В некоторых исследованиях, если 
- имитационная модель процесса, требуется вместо
нее получить так называемую "вторичную модель" в виде аналитической зависимости. В дальнейшем "вторичная модель" может быть использована на практике или в других исследованиях. В таких случаях математическая модель формируется по данным эксперимента методом регрессионного анализа, что будет предметом нашего рассмотрения в следующей теме.
Боев В.Д., Сыпченко Р.П. Компьютерное моделирование
|
|
 |
