Стандартные планы

Многие планы экспериментов в настоящее время стандартизованы. Они имеются в справочниках, математических пакетах программ и системах моделирования. Однако исследователь должен быть готов к модификации имеющихся планов и приспособлению их к специфическим условиям конкретных задач.

С полным факторным экспериментом мы уже знакомы. Это, как отмечалось ранее, самый информативный план, понятный по структуре, но и самый экономичный. Поэтому ПФЭ применяют, когда число факторов невелико. В приведенном примере 4.1 при

затраты времени на проведение компьютерного эксперимента ожидаются в 106 часов. Поэтому актуальной становится проблема более или менее обоснованного сокращения плана эксперимента (числа наблюдений). Способов сокращения плана и, следовательно, уменьшения затрат времени на проведение экспериментов, много, но все они, в конечном счете, основаны на пренебрежении эффектами парных, тройных и более взаимодействий факторов. Естественно, это снижает точность моделирования, но во многих случаях допустимо.

Пример 4.2. Необходимо провести эксперимент с моделью, имеющей три двухуровневых фактора, с целью построения математической модели ("вторичной модели") процесса в виде:

Уравнение имеет восемь коэффициентов, следовательно, достаточно провести восемь наблюдений. Это уравнение соответствует

Полный факторный эксперимент дает возможность определить не только коэффициенты

, соответствующие так называемым линейным эффектам (их также называют главными), но и коэффициенты

, соответствующие всем эффектам взаимодействия факторов, а также свободный член

Эффекты взаимодействия двух и более факторов проявляются, если влияние каждого из них на отклик зависит от уровней, на которых установлены другие факторы.

Теперь допустим, что число наблюдений в эксперименте, равное восьми, неприемлемо и план надо сократить.

Вполне естественно предположить, что эффекты взаимодействия оказывают на реакцию системы существенно меньшее влияние, чем линейные, или даже отсутствуют вовсе, если факторы обладают свойством независимости.

Исключим их и тогда модель процесса (уравнение отклика, уравнение реакции, "вторичная модель") принимает вид:

Теперь число неизвестных коэффициентов

сократилось вдвое и число необходимых наблюдений для их определения стало равно четырем.

Четыре наблюдения достаточны для проведения ПФЭ при двух

факторной модели

. Этими факторами, например, могут быть

или другая двухфакторная комбинация из трех факторов.

Уровни третьего фактора

получают из первых двух с помощью, так называемого генерирующего соотношения:

Поскольку факторы двухуровневые, то в общем виде уровни принято обозначать так:

Новый, сокращенный план эксперимента называют полурепликой и обозначают

План приведен в табл. 4.1.

Таблица 4.1. План ПФЭ 2^2
№		План ПФЭ			Отклик
№					Отклик
1	1	-1	-1	+1
2	1	+1	-1	-1
3	1	-1	+1	-1
4	1	+1	+1	+1

Единичный столбец

обеспечивает вычисление свободного члена

в модели процесса.

Таким же образом можно проводить дальнейшее сокращение планов типа

получая четверть реплики

и более мелкие реплики.

Естественно, такое сокращение числа экспериментов приводит к "огрублению" коэффициентов

Следовательно, полученную модель процесса

нужно проверять на адекватность, используя для этого "сэкономленные" наблюдения.

Рассмотренное планирование является основой и составной частью для разработки более сложных - несимметричных многоуровневых планов.

Не менее часто целью экспериментов является проверка разного рода гипотез о природе сравниваемых объектов. Например, однородны ли выходы двух систем в смысле законов распределения, характеристик этих законов. Поскольку обработка данных эксперимента ведется методами дисперсионного анализа, то и планы в данном случае называются планами дисперсионного анализа. Сущность дисперсионного анализа мы рассмотрим в следующей теме.

Планы дисперсионного анализа могут быть полные, если используются все возможные сочетания условий (аналогично ПФЭ), и неполные, которые применяются тогда, когда полные планы оказываются громоздкими и неэкономичными. Сокращение планов происходит, как и ранее, за счет исключения некоторых сочетаний факторов (взаимодействий) и уровней случайным или традиционным образом.

Наиболее популярными из неполных планов является симметричный план "латинский квадрат" или его вариации. Этот план целесообразно применять, когда из всех существенных факторов можно выделить один доминирующий (самый существенный).

В планах дисперсионного анализа часто факторы обозначают латинскими буквами

, а уровни - индексами при соответствующих факторах:

Пример 4.3. Построить план "латинский квадрат" симметричного трехфакторного четырехуровневого эксперимента. Доминирующий фактор

Таблица 4.2. План "латинский квадрат"
Уровни	Уровни
Уровни

В этом плане число наблюдений

В полном плане их было бы

Сокращение произошло за счет исключения некоторых комбинаций:

и др.

Заметим, что план может быть и несимметричным. В этом случае вместо квадрата будет прямоугольник. И еще: выделение доминирующего фактора не является существенным, то есть, внутри квадрата можно располагать уровни любого из действующих факторов.

В практике планирования экспериментов встречаются и такие неполные планы: один из факторов меняет свои значения при фиксированных значениях других. То есть исследуется поочередно влияние каждого фактора в отдельности.

Иногда применяются и так называемые рандомизированные планы. В таких планах сочетания факторов и уровней для каждого прогона модели выбираются случайно. Вид случайности и объем выборки определяется исследователем.

4.4. Формальный подход к сокращению общего числа прогонов

Рассмотренные способы сокращения общего числа прогонов носят эвристический (субъективный) характер. Они осуществлялись за счет исключения каких-то комбинаций уровней факторов.

Однако во многих случаях исследователь имеет свободу действий в выборе числа факторов

числа уровней

и числа прогонов

модели в одном наблюдении. Каждый из этих аргументов в конкретной ситуации по-разному влияет на общее число прогонов модели

Как нам уже известно, общее число прогонов (реализаций) модели равно:

Рассмотрим относительное влияние аргументов

на число реализаций

Сначала нужно получить выражения для вычисления скоростей изменения функции

при изменении одного аргумента и неизменных остальных аргументах. Для этого последовательно найдем частные производные первого порядка от функции

по этим аргументам:

Теперь сравним попарно полученные производные:

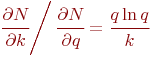
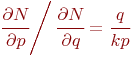
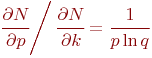
Из соотношений 1 и 2 следует: если

, то наибольшее влияние на число

оказывает изменение числа уровней

Из соотношений 3 и 1 следует: если

, то наибольшее влияние на число

оказывает изменение числа факторов

Из соотношений 2 и 3 следует: если

, то наибольшее влияние на число

оказывает изменение числа реализаций модели на каждом уровне факторов (на каждом наблюдении).

Рассмотренный формальный подход к сокращению числа реализаций не совсем корректен, так как функция общего числа прогонов

носит не непрерывный, а дискретный характер. Тем не менее, такой подход применяется с последующим округлением результатов до целых чисел.

Покажем применение формального подхода сокращения реализаций на примере.

Пример 4.4. На вход модели объекта действуют четыре трехуровневых фактора

В каждом наблюдении предполагаются восемь прогонов модели

Полный факторный эксперимент потребует

прогонов или 81 наблюдение. Такие затраты ресурсов неприемлемы.

Требуется определить, какой из аргументов

следует уменьшить, чтобы достичь наиболее существенного уменьшения числа реализаций

Следовательно, наибольшее влияние на изменение

оказывает изменение числа уровней

Уменьшим

на единицу:

. В этом случае при ПФЭ потребуется выполнить

прогонов или 16 наблюдений, то есть в пять раз меньше.

Варьирование факторов на двух уровнях встречается часто и решение

будет приемлемо, если нет обстоятельств, не устраивающих это решение.

Элементы тактического планирования

Основной задачей тактического планирования является обеспечение результатам компьютерного эксперимента заданных точности и достоверности.

Рассмотрим случай, когда имитационная модель строилась для определения характеристик некоторых случайных величин.

Характеристику случайной величины будем обозначать греческой буквой

С помощью имитационного моделирования точное значение

определить нельзя, так как число

реализаций модели конечно. При конечном числе реализаций модели определяется приближенное значение характеристики. Обозначим это приближение

Приближенное значение

называют оценка соответствующей характеристики: оценкой матожидания, оценкой дисперсии, оценкой коэффициента корреляции.

Точностью характеристики

называют величину

в отношении

Величина

представляет собой абсолютное значение ошибки в определении значения искомой характеристики.

Достоверность оценки характеристики

называют вероятность

того, что заданная точность достигается:

Достоверность характеризует повторяемость, устойчивость эксперимента и трактуется так: если для оценки

использовать величину

то в среднем на каждые 1000 применений этого правила в

случаев величина

будет отличаться от

на величину меньше

В ряде случаев целесообразно пользоваться понятием относительной точности

В этом случае достоверность оценки имеет вид:

Ссылки

Боев В.Д., Сыпченко Р.П. Компьютерное моделирование

Знаете ли Вы, что масштаб времени - это число, которое задает длительность моделирования одной единицы модельного времени, пересчитанной в секунды, в секундах астрономического реального времени при выполнении модели.