

  |
Метод Эйлера (Метод называют также методом ломаных, так как участки кривой функции заменяются отрезками прямых) является простейшим приближенным способом решения дифференциальных уравнений. Рассмотрим его геометрическую интерпретацию на примере одного уравнения
![]()
Пусть требуется проинтегрировать уравнение на интервале [a,b] т.е. найти профиль изменения функции y для заданного диапазона значений аргумента x (см. рис.).

Разделим интервал [a,b] на равные малые отрезки D x, называемые шагом интегрирования. На рисунке пунктиром обозначена неизвестная функция y, которую требуется найти. Мысленно проведем в точке касательную к функции. Приближенным значением функции y в точке с координатой a+D x, т.е. на конце первого отрезка будем считать точку пересечения касательной и перпендикуляра, восстановленного в этой точке. Тогда
y(a+D x)=y(a)+D xЧ tga .
Угол a – это угол наклона касательной, проведенной в точке a. Из геометрического смысла первой производной следует, что тангенс угла наклона касательной, проведенной в некоторой точке, численно равен первой производной, вычисленной в этой точке, т.е.
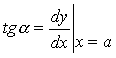 .
.
Формула для приближенного значения функции на конце отрезка принимает вид
 .
.
Вычислив значение функции после первого шага интегрирования, применим выведенную формулу для второго шага и т.д. Для произвольного шага i формула Эйлера принимает вид
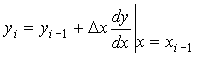 .
.
Таким образом, приближенное значение функции на конце текущего отрезка интегрирования равно сумме значения функции в начале отрезка и произведения шага интегрирования на величину производной, вычисленной в начале отрезка. Для первого шага должно быть известно значение функции в начале всего интервала интегрирования (в точке a), это значение называют начальным условием.
Для решения системы из p дифференциальных уравнений формулу Эйлера на каждом шаге интегрирования применяют для каждого из p уравнений.
Метод Эйлера достаточно прост для реализации, поэтому его часто программируют непосредственно в прикладной программе.
Пример решения уравнений методом Эйлера
Метод решения дифференциальных уравнений Рунге - Кутты
|
|