Пример. Рассмотрим в качестве примера, демонстрирующего интегрирование системы дифференциальных уравнений методом Эйлера непосредственно в программе пользователя, программу решения системы уравнений, описывающих кинетику химического взаимодействия в соответствии с реакцией
![]()
Здесь Aj – символическое обозначение реагентов, k1 и k2 – константы скоростей соответствующих реакций. В изотермических условиях константы скоростей постоянны и для режима идеального вытеснения
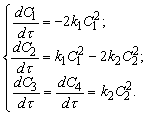
В приводимом ниже тексте программы используются процедуры для вывода таблиц (см. приложение 1).
Program Euler_test;
Uses Crt, Mathlib;
const
neq = 4;
var
nstep, i, j : byte;
h, x, k1, k2 : real;
c, dery : vector_20;
begin
Clrscr;
write('Константы скорости реакции k1, k2: ');
readln(k1,k2);
write('Число шагов интегрирования: ');
readln(nstep);
write('Шаг интегрирования: ');
readln(h);
write('Начальное значение аргумента: ');
readln(x);
write('Начальные условия: ');
for i := 1 to 4 do
read(c[i]);
Title(1,neq+1,' tau ',' c1 ',' c2 ',
' c3 ',' c4 ','','','','','');
Table(1,neq+1,x,c[1],c[2],c[3],c[4],x,x,x,x,x);
for i := 1 to nstep do begin
{Вычисление производных}
dery[1] := -2*k1*sqr(c[1]);
dery[2] := k1*sqr(c[1])-2*k2*sqr(c[2]);
dery[3] := k2*sqr(c[2]);
dery[4] := dery[3];
{Вычисление значений функций по Эйлеру}
for j := 1 to neq do
c[j] := c[j]+h*dery[j];
x := x+h; {Новое значение аргумента}
Table(1,neq+1,x,c[1],c[2],c[3],c[4],x,x,x,x,x);
end;
end.
Результат работы программы на экране будет иметь вид
Константы скорости реакции k1, k2: 0.3 0.7
Число шагов интегрирования: 10
Шаг интегрирования: 1
Начальное значение аргумента: 0
Начальные условия: 1 0.1 0 0
Т а б л и ц а 1
------------+-----------+-----------+-----------+-----------+
¦ ¦ ¦ ¦ ¦ ¦
¦ tau ¦ c1 ¦ c2 ¦ c3 ¦ c4 ¦
¦ ¦ ¦ ¦ ¦ ¦
+-----------+-----------+-----------+-----------+-----------+
¦ ¦ ¦ ¦ ¦ ¦
¦ 0.0000 ¦ 1.0000 ¦ 0.1000 ¦ 0.0000 ¦ 0.0000 ¦
¦ 1.0000 ¦ 0.4000 ¦ 0.3860 ¦ 0.0070 ¦ 0.0070 ¦
¦ 2.0000 ¦ 0.3040 ¦ 0.2254 ¦ 0.1113 ¦ 0.1113 ¦
¦ 3.0000 ¦ 0.2486 ¦ 0.1820 ¦ 0.1469 ¦ 0.1469 ¦
¦ 4.0000 ¦ 0.2115 ¦ 0.1542 ¦ 0.1700 ¦ 0.1700 ¦
¦ 5.0000 ¦ 0.1846 ¦ 0.1343 ¦ 0.1867 ¦ 0.1867 ¦
¦ 6.0000 ¦ 0.1642 ¦ 0.1193 ¦ 0.1993 ¦ 0.1993 ¦
¦ 7.0000 ¦ 0.1480 ¦ 0.1074 ¦ 0.2093 ¦ 0.2093 ¦
¦ 8.0000 ¦ 0.1349 ¦ 0.0979 ¦ 0.2174 ¦ 0.2174 ¦
¦ 9.0000 ¦ 0.1240 ¦ 0.0899 ¦ 0.2241 ¦ 0.2241 ¦
¦ 10.0000 ¦ 0.1147 ¦ 0.0832 ¦ 0.2297 ¦ 0.2297 ¦
Приводим вариант текста процедуры, реализующей метод Эйлера для решения системы дифференциальных уравнений. В процедуре предусмотрена передача через список параметров имени процедуры, вычисляющей вектор производных (процедура Right). Результат интегрирования выводится в виде таблицы процедурами Title и Table (см. приложение 1), управление выводом результатов осуществляется логической переменной PrintOn. Смысл остальных параметров поясняется в комментариях.
Type
derivatives = Procedure(x : real;
var Y , DERY : vector_20);
Procedure Euler(neq, {Число дифференциальных уравнений}
nstep : byte; {Число шагов интегрирования}
h, {Шаг интегрирования}
x : real; {Начальное значение аргумента}
var y : Vector_20; {Вектор значений функций}
PrintOn : boolean; {Управление выводом}
Right : derivatives); {Имя процедуры,
вычисляющей производные}
var
i, j : integer;
dery : vector_20;
begin
if PrintOn then begin
writeln(' Число уравнений - ',neq:3);
writeln(' Число шагов интегрирования -',nstep:3);
writeln(' Шаг интегрирования - ',h:10:3);
writeln(' Начальное значение аргумента - ',x:10:3);
writeln(' Начальные условия:');
for i := 1 to neq do
writeln('y[',i:3,'] = ',y[i]:10:3);
Table(1,neq+1,x,y[1],y[2],y[3],y[4],
y[5],y[6],y[7],y[8],y[9]);
end;
for j := 1 to nstep do begin
Right(x,y,dery);
for i := 1 to neq do
y[i] := y[i]+h*dery[i];
x := x+h;
if PrintOn then begin
Table(1,neq+1,x,y[1],y[2],y[3],y[4],
y[5],y[6],y[7],y[8],y[9]);
end;
end;
end { Euler };
Процедура Euler и описание процедурного типа derivatives помещены в библиотеку Mathlib.
Пример. Численное интегрирование системы дифференциальных уравнений предыдущего примера с использованием библиотечной процедуры Euler демонстрирует следующая программа.
Program Euler_test;
Uses Crt, Mathlib;
const
neq = 4;
var
nstep, i : byte;
h, x, k1, k2 : real;
c, dery : vector_20;
{Процедура, реализующая алгоритм вычисления производных}
Procedure fct( x : real;
var c, dery : vector_20);
begin
dery[1] := -2*k1*sqr(c[1]);
dery[2] := k1*sqr(c[1])-2*k2*sqr(c[2]);
dery[3] := k2*sqr(c[2]);
dery[4] := dery[3];
end;
begin
Clrscr;
write('Константы скорости реакции k1, k2: ');
readln(k1,k2);
write('Число шагов интегрирования: ');
readln(nstep);
write('Шаг интегрирования: ');
readln(h);
write('Начальное значение аргумента: ');
readln(x);
write('Начальные условия: ');
for i := 1 to 4 do
read(c[i]);
Assign(Output,'euler_te.res');
Rewrite(Output);
Euler(neq,nstep,h,x,c,true,fct);
end.
В приведенном примере программы вывод результатов осуществляется в дисковый файл euler_te.res, создаваемый в текущем каталоге:
Число уравнений - 4
Число шагов интегрирования - 10
Шаг интегрирования - 1.000
Начальное значение аргумента - 0.000
Начальные условия:
y[ 1] = 1.000
y[ 2] = 0.100
y[ 3] = 0.000
y[ 4] = 0.000
Т а б л и ц а 1
------------+-----------+-----------+-----------+-----------+
¦ ¦ ¦ ¦ ¦ ¦
¦ ¦ ¦ ¦ ¦ ¦
¦ ¦ ¦ ¦ ¦ ¦
+-----------+-----------+-----------+-----------+-----------+
¦ ¦ ¦ ¦ ¦ ¦
¦ 0.0000 ¦ 1.0000 ¦ 0.1000 ¦ 0.0000 ¦ 0.0000 ¦
¦ 1.0000 ¦ 0.4000 ¦ 0.3860 ¦ 0.0070 ¦ 0.0070 ¦
¦ 2.0000 ¦ 0.3040 ¦ 0.2254 ¦ 0.1113 ¦ 0.1113 ¦
¦ 3.0000 ¦ 0.2486 ¦ 0.1820 ¦ 0.1469 ¦ 0.1469 ¦
¦ 4.0000 ¦ 0.2115 ¦ 0.1542 ¦ 0.1700 ¦ 0.1700 ¦
¦ 5.0000 ¦ 0.1846 ¦ 0.1343 ¦ 0.1867 ¦ 0.1867 ¦
¦ 6.0000 ¦ 0.1642 ¦ 0.1193 ¦ 0.1993 ¦ 0.1993 ¦
¦ 7.0000 ¦ 0.1480 ¦ 0.1074 ¦ 0.2093 ¦ 0.2093 ¦
¦ 8.0000 ¦ 0.1349 ¦ 0.0979 ¦ 0.2174 ¦ 0.2174 ¦
¦ 9.0000 ¦ 0.1240 ¦ 0.0899 ¦ 0.2241 ¦ 0.2241 ¦
¦ 10.0000 ¦ 0.1147 ¦ 0.0832 ¦ 0.2297 ¦ 0.2297 ¦
|
|