© 2008 Алексей Померанцев
В этом пособии рассказывается о методе главных компонент (Principal Component Analysis, PCA) – базовом подходе, применяемом при анализе данных для решения разнообразных задач. Текст ориентирован, прежде всего, на специалистов в области анализа экспериментальных данных: химиков, физиков, биологов, и т.д. Он может служить пособием для исследователей, начинающих изучение этого вопроса. Продолжить изучение вопроса можно с помощью указанной Литературы
В пособии интенсивно используются понятия и методы матричной алгебры – вектор, матрица, и т.п. Читателям, которые плохо знакомы с этим аппаратом, рекомендуется изучить, или, хотя бы просмотреть, пособие "Матрицы и векторы".
Изложение иллюстрируется примерами, выполненными в рабочей книге Excel "People.xls" которая сопровождает этот документ.
Важная информация о работе с файлом People.xls
Ссылки на примеры помещены в текст как объекты Excel. По форме, эти примеры имеют абстрактный, модельный характер, однако, по сути, они тесно связаны с задачами, встречающимися на практике. Предполагается, что читатель имеет базовые навыки работы в среде Excel, умеет проводить простейшие матричные вычисления с использованием функций листа, таких как MMULT, TREND. Освежить эти знания можно с помощью пособия Матричные операции в Excel.
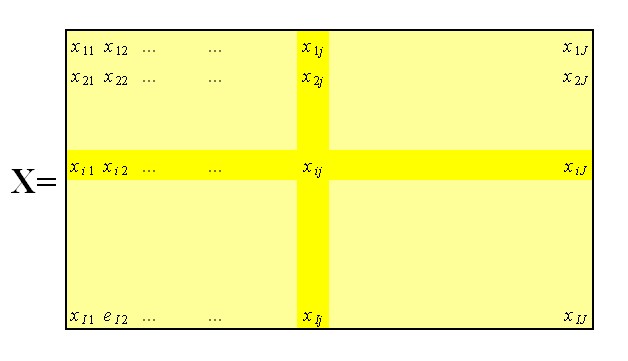
Метод главных компонент применяется к данным, записанным в виде матрицы X – прямоугольной таблицы чисел размерностью I строк и J столбцов.
Рис. 1 Матрица данных
Традиционно строки этой матрицы называются образцами. Они нумеруются индексом i, меняющимся от 1 до I. Столбцы называются переменными, и они нумеруются индексом j= 1, …, J.
Цель PCA – извлечение из этих данных нужной информации. Что является информацией, зависит от сути решаемой задачи. Данные могут содержать нужную нам информацию, они даже могут быть избыточными. Однако, в некоторых случаях, информации в данных может не быть совсем.
Размерность данных – число образцов и переменных – имеет большое значение для успешной добычи информации. Лишних данных не бывает – лучше, когда их много, чем мало. На практике это означает, что если получен спектр какого–то образца, то не нужно выбрасывать все точки, кроме нескольких характерных длин волн, а использовать их все, или, по крайней мере, значительный кусок.
Данные всегда (или почти всегда) содержат в себе нежелательную составляющую, называемую шумом. Природа этого шума может быть различной, но, во многих случаях, шум – это та часть данных, которая не содержит искомой информации. Что считать шумом, а что – информацией, всегда решается с учетом поставленных целей и методов, используемых для ее достижения.
Шум и избыточность в данных обязательно проявляют себя через корреляционные связи между переменными. Погрешности в данных могут привести к появлению не систематических, а случайных связей между переменными. Понятие эффективного (химического) ранга и скрытых, латентных переменных, число которых равно этому рангу, является важнейшим понятием в PCA
Постараемся передать суть метода главных компонент, используя интуитивно–понятную геометрическую интерпретацию. Начнем с простейшего случая, когда имеются только две переменные x1 и x2. Такие данные легко изобразить на плоскости (Рис. 2).
Рис. 2 Графическое представление двумерных данных
Каждой строке исходной таблицы (т.е. образцу) соответствует точка на плоскости с соответствующими координатами. Они обозначены пустыми кружками на Рис. 2. Проведем через них прямую, так, чтобы вдоль нее происходило максимальное изменение данных. На рисунке эта прямая выделена синим цветом; она называется первой главной компонентой – PC1. Затем спроецируем все исходные точки на эту ось. Получившиеся точки закрашены красным цветом. Теперь мы можем предположить, что на самом деле все наши экспериментальные точки и должны были лежать на этой новой оси. Просто какие–то неведомые силы отклонили их от правильного, идеального положения, а мы вернули их на место. Тогда все отклонения от новой оси можно считать шумом, т.е. ненужной нам информацией. Правда, мы должны быть в этом уверены. Проверить шум ли это, или все еще важная часть данных, можно поступив с этими остатками так же, как мы поступили с исходными данными – найти в них ось максимальных изменений. Она называется второй главной компонентой (PC2). И так надо действовать, до тех пор, пока шум уже не станет действительно шумом, т.е. случайным хаотическим набором величин.
В общем, многомерном случае, процесс выделения главных компонент происходит так:
Рис. 3 Графическое представление метода главных компонент
В результате, мы переходим от большого количества переменных к новому представлению, размерность которого значительно меньше. Часто удается упростить данные на порядки: от 1000 переменных перейти всего к двум. При этом ничего не выбрасывается – все переменные учитываются. В то же время несущественная для сути дела часть данных отделяется, превращается в шум. Найденные главные компоненты и дают нам искомые скрытые переменные, управляющие устройством данных.
Суть метода главных компонент – это существенное понижение размерности данных. Исходная матрица X заменяется двумя новыми матрицами T и P, размерность которых, A, меньше, чем число переменных (столбцов) J у исходной матрицы X
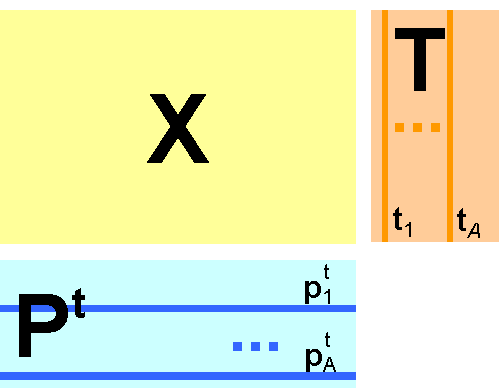
Вторая размерность – число образцов (строк) I сохраняется. Если декомпозиция выполнена правильно – размерность A выбрана верно, то матрица T несет в себе столько же информации, сколько ее было в начале, в матрице X. При этом матрица T меньше, и, стало быть, проще, чем X.
Пусть имеется матрица
переменных X размерностью (I×J), где I –
число образцов (строк), а J – это число
независимых переменных (столбцов),
которых, как правило, много (J>>1). В
методе главных компонент используются
новые, формальные переменные ta
(a=1,…A), являющиеся линейной
комбинацией исходных переменных xj
(j=1,…J)
С помощью этих новых переменных
матрица X разлагается в
произведение двух матриц T и P –
Матрица T называется матрицей счетов (scores). Ее размерность (I×A).
Матрица P называется матрицей нагрузок (loadings). Ее размерность (J×A).
E – это матрица остатков, размерностью (I×J).
Рис. 5 Разложение по главным компонентам
Новые переменные ta называются главными компонентами (Principal Components), поэтому и сам метод называется методом главных компонент (PCA). Число столбцов – ta в матрице T, и pa в матрице P, равно A, которое называется числом главных компонент (PC). Эта величина заведомо меньше числа переменных J и числа образцов I.
Важным свойством PCA является ортогональность (независимость) главных компонент. Поэтому матрица счетов T не перестраивается при увеличении числа компонент, а к ней просто прибавляется еще один столбец – соответствующий новому направлению. Тоже происходит и с матрицей нагрузок P.
Чаще всего для построения PCA счетов и нагрузок, используется рекуррентный алгоритм NIPALS, который на каждом шагу вычисляет одну компоненту. Сначала исходная матрица X преобразуется (как минимум – центрируется; см. раздел 2.12) и превращается в матрицу E0, a=0. Далее применяют следующий алгоритм.
- 1. Выбрать начальный вектор t
- 2. pt = tt Ea / ttt
- 3. p = p / (ptp)½
- 4. t = Ea p / ptp
- 5. Проверить сходимость, если нет, то идти на 2
После вычисления очередной (a-ой) компоненты, полагаем ta=t и pa=p. Для получения следующей компоненты надо вычислить остатки Ea+1 = Ea – t pt и применить к ним тот же алгоритм, заменив индекс a на a+1. Программа для реализации PCA в среде MatLab приведена в пособии MatLab. Руководство для начинающих .
В этом пособии для построения PCA используется специальная надстройка для программы Excel (Add–In) Chemometrics.xla. Она дополняет список стандартных функций Excel и позволяет проводить PCA разложение на листах рабочей книги. Подробности об этой программе можно прочитать в пособии Проекционные методы в системе Excel.
После того, как построено пространство из главных компонент, новые образцы Xnew могут быть на него спроецированы, иными словами – определены матрицы их счетов Tnew. В методе PCA это делается очень просто
Метод главных компонент тесно связан с другим разложением – по сингулярным значениям, SVD. В последнем случае исходная матрица X разлагается в произведение трех матриц
X=USVt
Здесь U – матрица, образованная ортонормированными собственными векторами ur матрицы XXt, соответствующим значениям λr;
XXtur = λrur;
V– матрица, образованная ортонормированными собственными векторами vr матрицы XtX;
XtXvr = λrvr;
S – положительно определенная диагональная матрица, элементами которой являются сингулярные значения σ1≥... ≥σR≥0 равные квадратным корням из собственных значений λr
![]()
Связь между PCA и SVD определяется следующими простыми соотношениями
T = US P = V
Матрица счетов T дает нам проекции исходных образцов (J –мерных векторов x1,…,xI) на подпространство главных компонент (A-мерное). Строки t1,…,tI матрицы T – это координаты образцов в новой системе координат. Столбцы t1,…,tA матрицы T – ортогональны и представляют проекции всех образцов на одну новую координатную ось.
При исследовании данных методом PCA, особое внимание уделяется графикам счетов. Они несут в себе информацию, полезную для понимания того, как устроены данные. На графике счетов каждый образец изображается в координатах (ti, tj), чаще всего – (t1, t2), обозначаемых PC1 и PC2. Близость двух точек означает их схожесть, т.е. положительную корреляцию. Точки, расположенные под прямым углом, являются некоррелироваными, а расположенные диаметрально противоположно – имеют отрицательную корреляцию.
Рис.6 График счетов
Подробнее о том, как из графиков счетов извлекается полезная информация, будет рассказано в примере.
Для матрицы счетов имеют место следующие соотношения –
TtT = Λ= diag{ λ1,…,λA},
где
величины λ1≥... ≥λA≥0
– это собственные значения. Они
характеризуют важность каждой
компоненты
Нулевое собственное значение λ0 определяется как сумма всех собственных значений, т.е.
Для вычисления PCA-счетов в надстройке Chemometrics Add-In используется функция ScoresPCA.
Матрица нагрузок P – это матрица перехода из исходного пространства переменных x1, …xJ (J-мерного) в пространство главных компонент (A-мерное). Каждая строка матрицы P состоит из коэффициентов, связывающих переменные t и x (1). Например, a-я строка – это проекция всех переменных x1, …xJ на a-ю ось главных компонент. Каждый столбец P – это проекция соответствующей переменной xj на новую систему координат.
Рис.7 График нагрузок
График нагрузок применяется для исследования роли переменных. На этом графике каждая переменная xj отображается точкой в координатах (pi, pj), например (p1, p2). Анализируя его аналогично графику счетов, можно понять, какие переменные связаны, а какие независимы. Совместное исследование парных графиков счетов и нагрузок, также может дать много полезной информации о данных.
В методе главных компонент нагрузки – это ортогональные нормированные вектора, т.е.
PtP = I
Для вычисления PCA-нагрузок в надстройке Chemometrics Add-In используется функция LoadingsPCA.
Результат моделирования методом главных компонент не зависит от порядка, в котором следуют образцы и/или переменные. Иными словами строки и столбцы в исходной матрице X можно переставить, но ничего принципиально не изменится. Однако, в некоторых случаях, сохранять и отслеживать этот порядок очень полезно – это позволяет лучше понять устройство моделируемых данных.
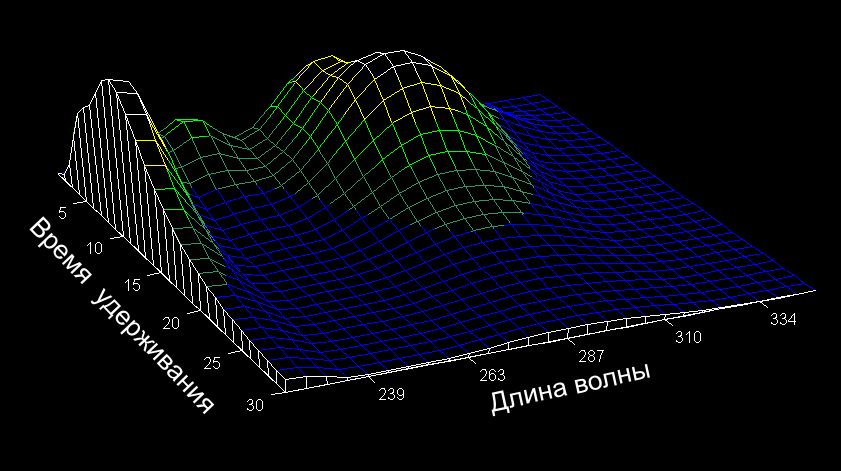
Рассмотрим простой пример – моделирование данных, полученных методом высокоэффективной жидкостной хроматографией с детектированием на диодной матрице (ВЭЖХ–ДДМ). Данные представляются матрицей, размерностью 30 образцов (I) на 28 переменных (J). Образцы соответствуют временам удерживания от 0 до 30 с, а переменные – длинам волн от 220 до 350 нм, на которых происходит детектирование. Данные ВЭЖХ–ДДМ представлены на Рис 8.
Эти данные хорошо моделируются методом PCA с двумя главными компонентами. Ясно, что в этом примере нам важен порядок, в котором идут образцы и переменные – он задается естественным ходом времени и спектральным диапазоном. Полученные счета и нагрузки полезно изобразить на графиках в зависимости от соответствующего параметра – счета от времени, а нагрузки от длины волны. (см. Рис 9)
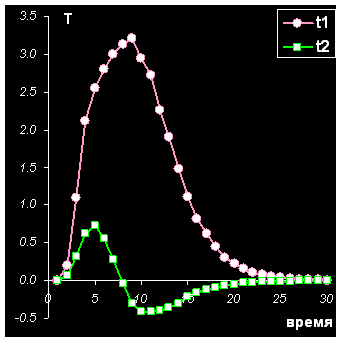
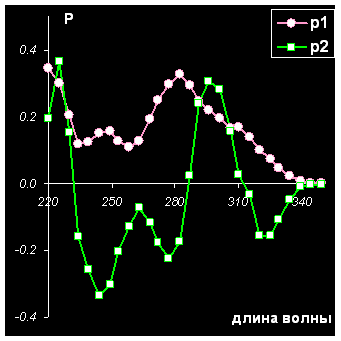
Рис. 9 Графики счетов и нагрузок для данных ВЭЖХ–ДДМ
Подробнее этот пример разобран в пособии Разрешение многомерных кривых .
PCA декомпозиция матрицы X является последовательным, итеративным процессом, который можно оборвать на любом шаге a=A. Получившаяся матрица
![]()
вообще говоря, отличается от матрицы X. Разница между ними
![]()
называется матрицей остатков.
Рассмотрим геометрическую интерпретацию остатков. Каждый исходный образец xi (строка в матрице X) можно представить как вектор в J– мерном пространстве с координатами
![]()
Рис. 10 Геометрия PCA
PCA проецирует его в вектор, лежащий в пространстве главных компонент, ti=(ti1, ti2, …tiA) размерностью A. В исходном пространстве этот же вектор ti имеет координаты
![]()
Разница между исходным вектором и его проекцией является вектором остатков
![]()
Он образует i–ю строку в матрице остатков E.
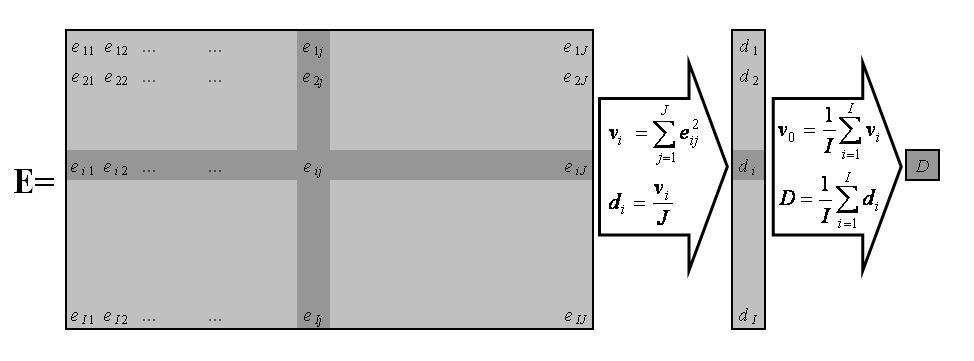
Рис.11 Вычисление остатков
Исследуя остатки можно понять, как устроены данные и хорошо ли они описываются PCA моделью.
Для вычисления PCA-остатков можно использовать приемы, описанные в пособии Расширение возможностей Chemometrics Add-In.
Величина –
определяет квадрат отклонения исходного вектора xi от его проекции на пространство PC. Чем оно меньше, тем лучше приближается i–ый образец.
Для вычисления отклонений можно использовать стандартные функции листа или специальную пользовательскую функцию.
Эта же величина, деленная на число переменных
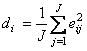
дает оценку дисперсии (вариации) i–го образца.
Среднее (для всех образцов) расстояние v0 вычисляется как
![]()
Оценка общая (для всех образцов) дисперсии вычисляется так –
![]()
В случае, когда PCA модель предназначена для предсказания или для классификации, а не для простого исследования данных, такая модель нуждается в подтверждении (валидации). При проверке методом тест–валидации исходный массив данных состоит из двух независимо полученных наборов, каждый из которых является достаточно представительным. Первый набор, называемый обучающим, используется для моделирования. Второй набор, называемый проверочным, служит только для проверки модели. Построенная модель применяется к данным из проверочного набора, и полученные результаты сравниваются с проверочными значениями. Таким образом принимается решение о правильности, точности моделирования.
Рис.12 Обучающий и проверочный наборы
В некоторых случаях объем данных слишком мал для такой проверки. Тогда применяют другой метод – перекрестной проверки (кросс–валидация), о котором можно прочитать здесь.
Используется также проверка методом коррекции размахом, суть которой предлагается изучить самостоятельно.
Результатом PCA моделирования
являются величины
![]() –
оценки, найденные по модели, построенной
на обучающем наборе Xc.
Результатом проверки служат величины
–
оценки, найденные по модели, построенной
на обучающем наборе Xc.
Результатом проверки служат величины
![]() –
оценки проверочных значений Xt,
вычисленные по той же модели, но как
новые образцы (3). Отклонение
оценки от проверочного значения
вычисляют как матрицу остатков: в
обучении
–
оценки проверочных значений Xt,
вычисленные по той же модели, но как
новые образцы (3). Отклонение
оценки от проверочного значения
вычисляют как матрицу остатков: в
обучении
![]() ,
,
и в проверке
![]() .
.
Следующие величины характеризуют "качество" моделирования в среднем.
Полная
дисперсия остатков в обучении (TRVC) и в
проверке (TRVP) –
|
|
|
Полная дисперсия выражается в тех же единицах (точнее их квадратах), что и исходные величины X.
Объясненная
дисперсия остатков в обучении (ERVC) и в
проверке (ERVP)
Объясненная дисперсия – это относительная величина. При ее вычислении используется естественная нормировка – сумма квадратов всех исходных величин xij. Обычно она выражается в процентах или в долях единицы. Во всех этих формулах величины eij – это элементы матриц Ec или Et. Для характеристик, наименование которых оканчивается на C (например, TRVC), используется матрица Ec (обучение), а для тех, которые оканчиваются на P (например, TRVP), берется матрица Et (проверка).
Как уже отмечалось выше, метод главных компонент – это итерационная процедура, в которой новые компоненты добавляются последовательно, одна за другой. Важно знать, когда остановить этот процесс, т.е. как определить правильное число главных компонент, A. Если это число слишком мало, то описание данных будет не полным. С другой стороны, избыточное число главных компонент приводит к переоценке, т.е. к ситуации, когда моделируется шум, а не содержательная информация.
Для выбора значения числа главных компонент обычно используется график, на котором объясненная дисперсия (ERV) изображается в зависимости от числа PC. Пример такого графика приведен на Рис. 13.
Рис. 13 Выбор числа PC
Из этого графика видно, что правильное число PC – это 3 или 4. Три компоненты объясняют 95%, а четыре 98% исходной вариации. Окончательное решение о величине A можно принять только после содержательного анализа данных.
Другим полезным инструментом является график, на котором изображаются собственные значения (4) в зависимости от числа PC. Пример показан на Рис.14.
Рис. 14 График собственных значений
Из этого рисунка опять видно, что для a=3 происходит резкое изменение формы графика – излом. Поэтому верное число PC – это три или четыре.
Разложение по методу главных компонент
![]()
не
является единственным. Вместо матриц T
и P можно использовать другие
матрицы
![]() и
и
![]() ,
которые дадут аналогичную декомпозицию
,
которые дадут аналогичную декомпозицию
![]()
с той же матрицей ошибок E. Простейший пример – это одновременное изменение знаков у соответствующих компонент векторов ta и pa, при котором произведение
![]()
остается неизменным. Алгоритм NIPALS дает именно такой результат – с точностью до знака, поэтому его реализация в разных программах может приводить к расхождениям в направлениях главных компонент.
Более сложный случай – это одновременное вращение матриц T и P. Пусть R – это ортогональная матрица вращения размерностью A×A , т.е такая матрица, что Rt=R–1. Тогда
![]()
Заметим, что новые матрицы счетов и нагрузок сохраняют все свойства старых,
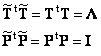 .
.
Это свойство PCA называется вращательной неопределенностью. Оно интенсивно используется при решении задач разделения кривых, в частности методом прокрустова вращения. Если отказаться от условий ортогональности главных компонент, то декомпозиция матрицы станет еще более общей. Пусть теперь R – это произвольная невырожденная матрица размерностью A×A . Тогда
![]()
Эти матрицы счетов и нагрузок уже не удовлетворяют условию ортогональности и нормирования. Зато они могут состоять только из неотрицательных элементов, а также подчиняться другим требованиям, накладываемым при решении задач разделения сигналов.
Во многих случаях, перед применением PCA, исходные данные нужно предварительно подготовить: отцентрировать и/или отнормировать. Эти преобразования проводятся по столбцам – переменным.
Центрирование – это вычитание из каждого столбца xj среднего (по столбцу) значения
![]() .
.
Центрирование необходимо потому, что оригинальная PCA модель (2) не содержит свободного члена.
Второе простейшее преобразование данных – это нормирование. Это преобразование выравнивает вклад разных переменных в PCA модель. При этом преобразовании каждый столбец xj делится на свое стандартное отклонение.
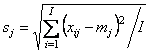
Комбинация центрирования и нормирования по столбцам называется автошкалированием.
![]()
Любое преобразование данных – центрирование, нормирование, и т.п. – всегда делается сначала на обучающем наборе. По этому набору вычисляются значения mj и sj, которые затем применяются и к обучающему, и к проверочному набору.
В надстройке Chemometrics Add In подготовка данных проводится автоматически. Если подготовку нужно провести вручную, то для нее можно использовать стандартные функции листа или специальную пользовательскую функцию.
В задачах, где структура исходных данных X априори предполагает однородность и гомоскедастичность, подготовка данных не только не нужна, но и вредна. Именно такой случай представляют ВЭЖХ–ДДМ данные, рассмотренные в пособии Разрешение многомерных кривых.
При заданном числе главных компонент A, величина

называется размахом (leverage). Эта величина равна квадрату расстояния Махаланобиса от центра модели до i–го образца в пространстве счетов, поэтому размах характеризует как далеко находится каждый образец в гиперплоскости главных компонент.
Для размаха имеет место соотношение
![]()
которое выполняется тождественно – по построению PCA.
Для вычисления размахов можно использовать стандартные функции листа или специальную пользовательскую функцию.
Другой важной характеристикой PCA модели является отклонение vi, которое вычисляется как сумма квадратов остатков (6) – квадрат эвклидова расстояния от плоскости главных компонент до объекта i.
Для вычисления отклонений можно использовать стандартные функции листа или специальную пользовательскую функцию.
Две эти величины: hi и vi определяют положение объекта (образца) относительно имеющейся PCA модели. Слишком большие значения размаха и/или отклонения свидетельствуют об особенности такого объекта, который может быть экстремальным или выпадающим образцом.
Анализ величин hi и vi составляет основу SIMCA – метода классификации с обучением.
Метод главных компонент иллюстрируется примером, помещенным в файл People.xls.
Этот файл включает в себя следующие листы:
Intro: краткое введение
Layout: схемы, объясняющая имена массивов, используемых в примере
Data: данные, используемые в примере.
MVA: PCA декомпозиция, выполненная с помощью надстройки Chemometrics.xla
PCA: копия всех результатов PCA не привязанная к надстройке Chemometrics.xla
Scores1–2: анализ младших счетов PC1–PC2
Scores3–4: анализ старших счетов PC3–PC4
Loadings: анализ нагрузок
Residuals: анализ остатков
Анализ базируется на данных европейского демографического исследования, опубликованных в книге К. Эсбенсена.
По причинам дидактического характера используется лишь небольшой набор из 32 человек, из которых 16 представляют Северную Европу (Скандинавия) и столько же – Южную (Средиземноморье). Для баланса выбрано одинаковое количество мужчин и женщин – по 16 человек. Люди характеризуются двенадцатью переменными, перечисленными в Табл. 1.
Табл. 1
Переменные, использованные в
демографическом анализе
| Height | Рост: в сантиметрах |
| Weight | Вес: в килограммах |
| Hair | Волосы: короткие: –1, или длинные: +1 |
| Shoes | Обувь: размер по европейскому стандарту |
| Age | Возраст: в годах |
| Income | Доход: в тысячах евро в год |
| Beer | Пиво: потребление в литрах в год |
| Wine | Вино: потребление в литрах в год |
| Sex | Пол: мужской: –1, или женский: +1 |
| Strength | Сила: индекс, основанный на проверке физических способностей |
| Region | Регион: север : –1, или юг: +1 |
| IQ | Коэффициент интеллекта, измеряемый по стандартному тесту |
Заметим, что такие переменные, как Sex, Hair и Region имеют дискретный характер с двумя возможными значениями: –1 или +1, тогда как остальные девять переменных могут принимать непрерывные числовые значения.
Рис. 15 Исходные данные в примере People
Прежде всего, любопытно посмотреть на графиках, как связаны между собой все эти переменные. Зависит ли рост (Height ) от веса (Weight)? Отличаются ли женщины от мужчин в потреблении вина (Wine)? Связан ли доход (Income) с возрастом (Age)? Зависит ли вес (Weight) от потребления пива (Beer)?
Рис.
16 Связи между переменными в примере People.
Женщины (F) обозначены кружками ●
и ●,
а мужчины (M) – квадратами ■
и ■.
Север (N) представлен голубым ■,
а юг (S) – красным цветом ●.
Некоторые из этих зависимостей показаны на Рис.16. Для наглядности на всех графиках использованы одни и те же обозначения: женщины (F) показаны кружками, мужчины (M) – квадратами, север (N) представлен голубым, а юг (S) – красным цветом.
Связь между весом (Weight) и ростом (Height) показана на Рис.16a. Очевидна, прямая (положительная) пропорциональность. Учитывая маркировку точек, можно заметить также, что мужчины (M) в большинстве своем тяжелее и выше женщин (F).
На Рис. 16b показана другая пара переменных: вес (Weight) и пиво (Beer). Здесь, помимо очевидных фактов, что большие люди пьют больше, а женщины – меньше, чем мужчины, можно заметить еще две отдельные группы – южан и северян. Первые пьют меньше пива при том же весе.
Эти же группы заметны и на Рис.16c, где показана зависимость между потреблением вина (Wine) и пива (Beer). Из него видно, что связь между этими переменными отрицательна – чем больше потребляется пива, тем меньше вина. На юге пьют больше вина, а на севере – пива. Интересно, что в обеих группах женщины располагаются слева, но не ниже по отношению к мужчинам. Это означает, что, потребляя меньше пива, прекрасный пол не уступает в вине.
Последний график на Рис. 16d показывает, как связаны возраст (Age) и доход (Income). Легко видеть, что даже в этом сравнительно небольшом наборе данных есть переменные, как с положительной, так и с отрицательной корреляцией.
Можно ли построить графики для всех пар переменных выборки? Вряд ли. Проблема состоит в том, что для 12 переменных существует 12(12–1)/2=66 таких комбинаций.
Перед тем, как подвергнуть данные анализу методом главных компонент, их надо подготовить. Простой статистический расчет показывает, что они нуждаются в автошкалировании (См. Рис. 17)
Рис. 17 Средние значения и СКО для переменных в примере People.
Средние значения по многим переменным отличаются от нуля. Кроме того, среднеквадратичные отклонения сильно разнятся. После автошкалирования среднее значение всех переменных становится равно нулю, а отклонение – единица.
Рис. 18 Автошкалированные данные в примере People.
В принципе, данные можно было бы не преобразовывать явно, на листе, а оставить как есть. Ведь стандартные аналитические процедуры, собранные в программе Chemometrics могут центрировать и шкалировать данные при выполнении вычислений. Однако матрица автошкалированных данных понадобится нам при вычислении остатков в разделе 3.8 .
Для построения PCA декомпозиции можно воспользоваться стандартными функциями ScoresPCA и LoadingsPCA, имеющимися в надстройке Chemometrics. Мы вычислим все 12 возможных главных компонент. В качестве первого аргумента используется исходный, не преобразованный массив данных, поэтому последний аргумент в обеих функциях равен 3 – автошкалирование.
Рис. 19 Вычисление матрицы счетов
Рис. 20 Вычисление матрицы нагрузок
В этом пособии все PCA вычисления проводятся в книге People.xls на листе MVA. Для удобства читателя эти же результаты продублированы на листе PCA как числа, без ссылки на надстройку Chemometrics.xla. Остальные листы рабочей книги связаны не с данными на листе MVA, с данными на листе PCA. Поэтому файл People.xls можно использовать даже тогда, когда надстройка Chemometrics.xla не установлена на компьютере.
Посмотрим на графики счетов, которые показывают, как расположены образцы в проекционном пространстве.
На графике младших счетов PC1–PC2 (Рис. 21) мы видим четыре отдельные группы, разложенные по четырем квадрантам: слева – женщины (F), справа – мужчины (M), сверху – юг (S), а снизу – север (N). Из этого сразу становится ясен смысл первых двух направлений PC1 и PC2. Первая компонента разделяет людей по полу, а вторая – по месту жительства. Именно эти факторы наиболее сильно влияют на разброс свойств.
Рис. 21 График счетов (PC1 – PC2) с обозначениями, использованными ранее на Рис 16
Продолжим изучение, построив график старших счетов PC3– PC4 (Рис. 22 ).
Рис.
22 График счетов (PC3 – PC4) с новыми
обозначениями:
размер и цвет символов отражает доход –
чем больше и светлее, тем он больше.
Числа представляют возраст
Здесь уже не видно таких отчетливых групп. Тем не менее, внимательно исследовав этот график совместно с таблицей исходных данных, можно, после некоторых усилий, сделать вывод о том, что PC3 отделяет старых/богатых людей от молодых/бедных. Чтобы сделать это более очевидным, мы изменили обозначения. Теперь каждый человек показан кружком, цвет и размер которого меняется в зависимости от дохода – чем больше и светлее, тем больше доход. Рядом показан возраст каждого объекта. Как видно, возраст и доход уменьшается слева направо, т.е. вдоль PC3. А вот смысл PC4 нам по–прежнему не ясен.
Чтобы разобраться с этим, построим соответствующие графики нагрузок. Они подскажут нам, какие переменные и как связаны между собой, что влияет на что.
Из графика младших компонент мы сразу видим, что переменные рост (Height), вес (Weight), сила (Strength) и обувь (Shoes) образуют компактную группу в правой части графика. Они практически сливаются, что означает их тесную положительную корреляцию. Переменные волосы (Hair) и пол (Sex) находятся в другой группе, лежащей по диагонали от первой группы. Это свидетельствует о высокой отрицательной корреляции между переменными из этих групп, например, силой (Strength) и полом (Sex). Наибольшие нагрузки на вторую компоненту имеют переменные вино (Wine) и регион (Region), также тесно связанные друг с другом. Переменная доход (Income) лежит на первом графике напротив переменной регион (Region), что отражает дифференциацию состоятельности: Север–Юг. Можно заметить также и антитезу переменных пиво (Beer) –регион/вино(Region/Wine).
Рис. 23 Графики нагрузок: PC1 – PC2 и PC3 – PC4
Из второго графика мы видим большие нагрузки переменных возраст (Age) и доход (Income) на ось PC3, что соответствует графику счетов на Рис. 21. Рассмотрим, переменные пиво (Beer) и IQ. Первая из них имеет большие нагрузки как на PC1, так и на PC2, фактически формируя диагональ взаимоотношений между объектами на графике счетов. Переменная IQ не обнаруживает связи с другими переменным, так как ее значения близки к нулю для нагрузок первых трех PC, и проявляет она себя только в четвертой компоненте. Мы видим, что значения IQ не зависят от места жительства, физиологических характеристик и пристрастий к напиткам.
Впервые PCA был применен еще в начале 20–го века в психологических исследованиях, когда верили, что такие показатели, как IQ или криминальное поведение можно объяснить с помощью индивидуальных физиологических и социальных характеристик. Если сравнить результаты PCA с графиками, построенными нами ранее для пар переменных, видно, что PCA сразу дает всеобъемлющее представление о структуре данных, которое можно "охватить одним взглядом" (точнее, с помощью четырех графиков). Поэтому, одна из наиболее сильных сторон PCA в исследовании структур данных – это переход от большого числа не связанных между собой графиков пар переменных к очень небольшому числу графиков счетов и нагрузок.
Сколько главных компонент нужно использовать в этом примере? Для ответа на вопрос нужно исследовать, как изменяется качество описания при увеличении числа PC. Заметим, что в этом примере мы не будем проводить проверку – в этом нет необходимости, т.к. PCA модель нужна только для исследования данных. Она не будет использоваться далее для прогнозирования, классификации, и т.п.
Рис. 24 Графики собственных значений
На Рис.24 показано, как, в зависимости от числа PC, меняются собственные значения λ . Видно, что около PC=5 происходит изменение в их поведении. Для расчета показателей TRV и ERV можно получить матрицу остатков E для каждого числа главных компонент A и вычислить требуемые показатели. Пример такого расчета для значения A=4 приведен на листе Residuals.
Рис. 25 Анализ остатков
Однако те же характеристики можно получить и проще, если воспользоваться соотношениями

Эти величины представлены на Рис. 26
Рис. 26 Графики полной (TRV) и объясненной (ERV) дисперсии остатков
Из этих зависимостей видно, что для описания данных достаточно четырех PC – они моделируют 94% данных, или, иными словами, шум, оставшийся после проекции на четырехмерное пространство PC1–PC4, оставляет всего 6% от исходных данных.
Рассмотренный пример позволил взглянуть лишь на малую часть возможностей, предоставляемых PCA–моделированием. Мы рассмотрели задачу исследования данных, которая не предполагает дальнейшего использования построенной модели для предсказания или классификации.
Метод PCA дает основу разнообразным методам, применяемым при обработке данных. В задачах классификации – это метод SIMCA, в задачах калибровки – это метод PCR, в задачах разделения кривых – это EFA, WFA и т.д.
|
|