c 2009 Алексей Померанцев
В этом документе рассмотрены наиболее популярные методы, применяемые для решения задач разрешения многомерных кривых (multivariate curve resolution). Текст ориентирован, прежде всего, на специалистов в области анализа экспериментальных данных: химиков, физиков, биологов, и т.д. Он может служить пособием для исследователей, начинающих изучение этого вопроса. Продолжить исследования можно с помощью указанной литературы.
В пособии интенсивно используются понятия и методы, описанные в других материалах по хемометрике: статистика, матрицы и векторы, метод главных компонент. Читателям, которые плохо знакомы с этим аппаратом, рекомендуется изучить, или, хотя бы просмотреть, эти материалы. Кроме того, здесь интенсивно используется специальная надстройка (Add-In) к программе Excel, которая называется Chemometrics.xla. Подробности об этой программе можно прочитать в пособии Проекционные методы в системе Excel.
Изложение иллюстрируется примерами, выполненными в рабочей книге Excel “MCR.xls”, которая сопровождает этот документ. Предполагается, что читатель имеет базовые навыки работы в среде Excel, умеет проводить простейшие матричные вычисления с использованием функций листа, таких как МУМНОЖ, ТЕНДЕНЦИЯ и т.п.
В отличие от других пособий из серии, здесь не удается один раз провести проекционные вычисления, а затем использовать их в разных методах. Поэтому некоторые листы книги MCR.xls не будут работать без использования Chemometrics Add-In.
Важная информация о работе с файлом MCR.xls
Ссылки на примеры помещены в текст как объекты Excel. По форме эти примеры имеют абстрактный, модельный характер, однако, по своей сути, они тесно связаны с задачами, встречающимися на практике.
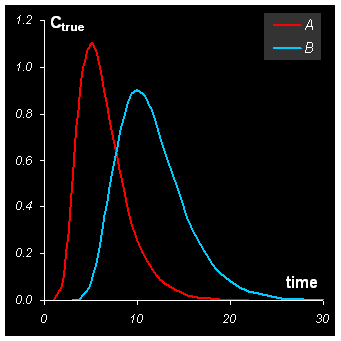
Рассмотрим систему, состоящую из нескольких веществ (компонент), A, B, … , концентрации которых cA, cB,… закономерно изменяются со временем t. Причиной изменения может быть химическая реакция, тогда c(t) – это кинетика. Другой случай – хроматографический эксперимент, тогда c(t) – это профиль элюции.– .
Рис. 1 Концентрационные профили
С другой стороны каждый компонент может быть охарактеризован своим чистым спектром (понимаемым в обобщенном виде) sA(λ), sB(λ),…., где λ – это длина волны. .
Рис. 2 Спектры чистых компонентов
По ходу эксперимента, в момент времени ti, на длине волны λj измеряется величина
x(ti, λj)=cA(ti) sA(λj)+cB(ti) sB(λj)+ ....
равная линейной суперпозиции всех спектров и концентраций "чистых" компонентов.
Рис. 3 Смешанные данные
Пусть I – это число наблюдений по времени: t1,….tI, а J – это число длин волн: λ1,…,λJ. Тогда данные, получаемые в эксперименте, можно представить в матричном виде
|
(1) |
Здесь матрицы данных X и погрешностей E имеют размерность I×J . Если в системе присутствует A химических компонентов, то матрица концентраций C имеет I строк и A столбцов. Каждый ее столбец – это профиль изменения концентрации соответствующего вещества. Матрица чистых спектров St (ее удобнее представлять в транспонированном виде) имеет A строк и J столбцов. Каждая ее строка – это чистый спектр соответствующего компонента.
Задача разрешения кривых (MCR) состоит в том, чтобы по заданной матрице данных X определить число химических компонентов (A) и найти матрицы концентраций C и чистых спектров S. При этом предполагается, что мы не обладаем никакими существенными априорными знаниями о матрицах C и S, кроме самых общих, естественных ограничений: неотрицательность, непрерывность (по t и λ), и т.п.
Разумеется, в такой постановке решение может не существовать, оно может быть неединственным. Все это будет обсуждено ниже. .
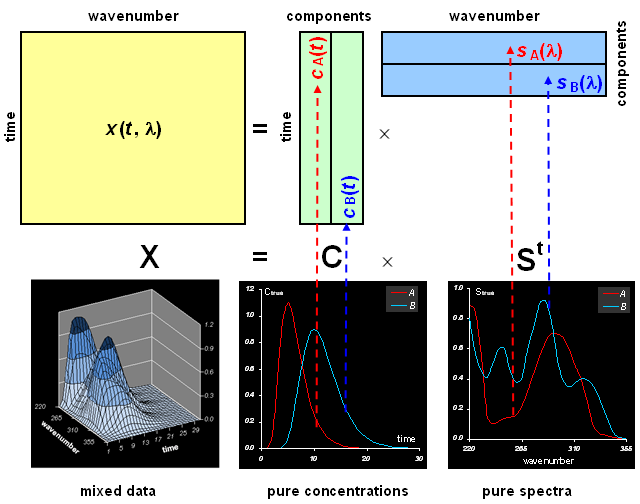
Рис. 4 Структура "хроматографических" данных
Допустим, что решение задачи (1) существует, т.е. имеется пара матриц C и S, приближающая исходную матрицу X
X = CSt + E.
Известно,
однако, что эта пара всегда не единственная. Вместо матриц C
и S можно использовать другие матрицы
![]() и
и
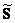 , которые дадут аналогичную
декомпозицию
, которые дадут аналогичную
декомпозицию
![]()
с той же матрицей ошибок E
Два типа неопределенности являются наиболее важными.
Пусть R – это ортогональная матрица вращения размерностью A×A, т.е такая матрица, что Rt=R–1. Тогда
|
(2) |
Этот тип неоднозначности называется вращательной неопределенностью. Этот факт означает, что, в принципе, имеется бесконечное число решений для задачи MCR, и некоторые из этих решений имеют физический смысл (например, неотрицательность), а другие нет. Использование вращательной неопределенности может быть очень полезным. Она позволяет выделять разумные решения задачи MCR. Ниже будет приведен соответствующий пример.
Помимо вращательной, имеется и масштабная неопределенность. В этом случае матрица R диагональная. Тогда
|
(3) |
Избавиться от масштабной неопределенности нельзя. Любое найденное решение будет определено только с точностью до умножения на константу,
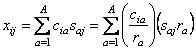
Иными словами каждый профиль концентраций ca может быть в ra раз меньше, если соответствующий чистый спектр sa увеличен в ra раз. Однако форма кинетики и спектра при этом сохраняется.
Как известно, невырожденную квадратную матрицу можно однозначно представить в виде полярного разложения. Поэтому любая неоднозначность сводится к комбинации масштабирования и вращения.
Задача MCR может не иметь решения. Для объяснения условий существования введем понятие концентрационного (спектрального) окна для химического компонента a. Окно – это область переменных (соответственно t или λ для которых величина соответствующего чистого сигнала (кинетики или спектра) больше нуля.
Существование решения задачи MCR зависит от того, как перекрываются окна разных химических компонент. Манне установил необходимые условия разрешимости в двух следующих теоремах.
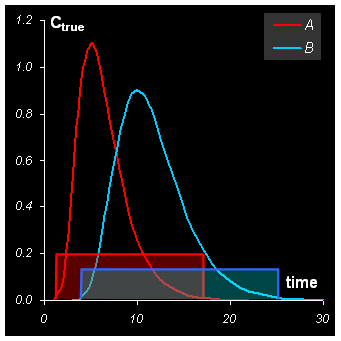
Рис. 5 Концентрационные окна
1. Концентрационный профиль химического компонента может быть восстановлен, если все остальные концентрационные окна, пересекающиеся с окном этого компонента, имеют участки вне этого окна.
2. Спектральный профиль химического компонента может быть восстановлен, если его концентрационное окно не находится целиком внутри концентрационного окна какого-нибудь другого компонента.
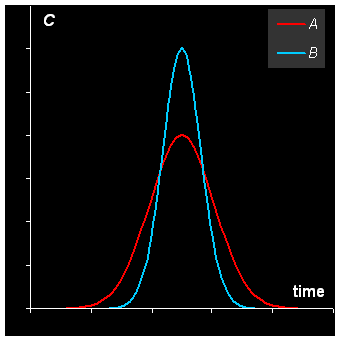
Рис.6 Вложенные концентрационные окна
Рис. 6 иллюстрирует эти утверждения. Видно, что концентрационное окно для компонента B целиком лежит внутри окна для A. Поэтому можно восстановить концентрационный профиль B, но нельзя найти его чистый спектр. С другой стороны для A можно найти чистый спектр, но нельзя найти концентрационный профиль.
Совершенно аналогичные теоремы справедливы при замене всех слов "концентрационный" на "спектральный", и наоборот. Это общее свойство задачи MCR – инвариантность относительно замены C на S, и S на C.
Методы MCR могут быть применены к экспериментальным данным самого разного вида, в том числе и к многомодальным данным. Однако есть два класса данных, где MCR применяется чаще всего. Это – данные "хроматографического" и "кинетического" типа. .
Данные хроматографического типа характеризуется наличием концентрационных окон, при отсутствии окон спектральных. Пример таких данных приведен выше (Рис. 4). Напротив, кинетические данные, как правило, не имеют концентрационных окон, но имеют спектральные окна.
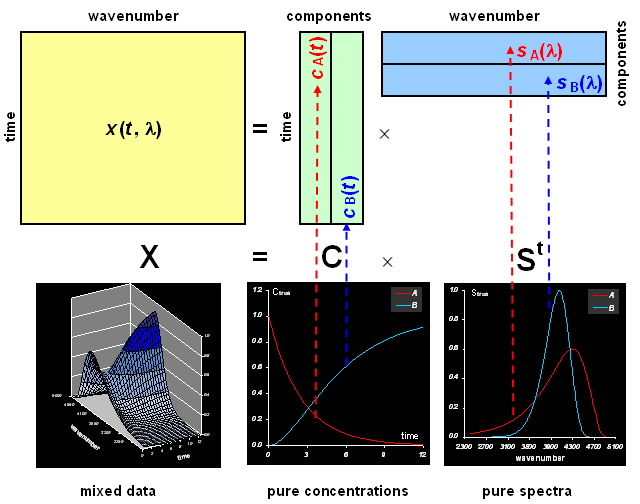
Рис.7 Моделирование "кинетических" данных
Пример кинетических данных показан на Рис. 7. В этом пособии будут рассмотрены только данные "хроматографического" типа. Тем не менее, все приведенные методы могут быть использованы и для "кинетических" данных. Для этого достаточно транспонировать исходную задачу MCR (1),
Xt = SCt + Et
Тогда спектры становятся "концентрациями", а концентрации – "спектрами". После этого все методы, справедливые для "хроматографических" задач, можно применять и к "кинетическим". Заметим, что и теоремы Манне сформулированы именно таким, инвариантным образом.
Разумеется, с химической точки зрения исходные данные могут иметь самое разное происхождение. Так, например, если спектры были получены в ходе титрования раствора в постоянных условиях, то концентрации изменяются в зависимости не от времени, а от другого параметра, например, pH раствора. Но сути дела это не меняет – главное, чтобы этот параметр менялся непрерывно и монотонно.
Предположим, что в задаче MCR (1) известна одна из двух матриц: C или S. Тогда вторую матрицу можно легко восстановить по исходной матрице X
Если известна матрица S то,
а если известна матрица C то,
В методе главных компонент (Principal Component Analysis, PCA) матрица данных X (I×J) также раскладывается в произведение двух матриц
Матрица T, размерностью (I×A), называется матрицей счетов (scores). Матрица P, размерностью (J×A), называется матрицей нагрузок (loadings). Число столбцов – ta в матрице T, и pa в матрице P – равно A. Это число называется числом главных компонент..
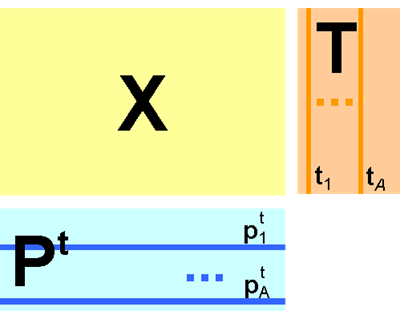
Рис.8
Графическое представление метода главных компонент
Следует различать химический компонент (мужской род) A, B, …, присутствующий в изучаемой системе, и главную компоненту (женский род), PC1, PC2,…, определяемую в методе PCA. Первый – это реальное вещество, имеющее свой спектр, а вторая – это абстрактная величина, характеризуемая вектором нагрузок. Но, в тоже время, между ними есть и много общего. Об этой пойдет речь ниже.
Для матрицы счетов T имеет место следующее соотношение TtT = Λ = diag{λ1,…,λA}, где величины λ1 >…>λA >0 называются собственными значениями. Они характеризуют вклад каждой компоненты в разложение
Нулевое собственное значение λ0 определяется как сумма всех собственных значений, т.е.
Квадратный корень из соответствующего собственного значения
называется сингулярным значением.
Число главных компонент является важнейшей характеристикой исследуемых данных, определяющей их сложность. Для оценки величины A применяются различные методы, основанные на анализе поведения системы при увеличении числа главных компонент. Применительно к задачам MCR можно выделить два подхода – анализ графика собственных значений и графиков нагрузок.
Между разложением PCA и задачей MCR имеется не только внешнее, а гораздо более глубокое сходство. Прежде всего, PCA позволяет оценить важнейший параметр – число химических компонентов в MCR, которое естественно равно числу главных компонент в PCA. Кроме того PCA дает базис для целого класса методов разрешения кривых, называемых факторным анализом. Слово "базис" здесь нужно понимать буквально – матрица счетов T и матрица концентраций C образуют одно и то же линейное подпространство. Аналогично обстоит дело и для матриц нагрузок P и чистых спектров S: Это означает, что оценка матрицы чистых спектров S может быть найдена как линейная комбинация векторов из матрицы нагрузок P, и, соответственно, оценка матрицы концентрационных профилей C может быть составлена из векторов счетов матрицы T. В связи с этим, говорят даже, что векторы PCA счетов и нагрузок являются абстрактными концентрационными профилями и спектрам
Для иллюстрации и сравнения различных методов разделения кривых будем использовать модельный пример, помещенный в рабочую книгу MCR.xls.
Эта книга включает в себя следующие листы:
Intro: краткое введение
Layout: схемы, объясняющая имена массивов, используемых в примере
Profiles: истинные концентрационные профили C
Spectra: истинные чистые спектры S
Data: модельные данные, используемые в примере. Блок X получен по формуле (1) с ошибками, которые формируются случайным образом на этой же странице.
Scores: PCA счета
Loadings: PCA нагрузки
Number PCs: определение числа главных компонент
Procrustes: Прокрустов анализ
EFA: Эволюционный факторный анализ
WFA: Оконный факторный анализ
ITTFA: Итерационный целевой факторный анализ
ALS: Чередующиеся наименьшие квадраты
Прообразом для модельного примера служит задача разделения пиков в высокоэффективной жидкостной хроматографии с детектированием на диодной матрице (ВЭЖХ-ДДМ). Известно, что в таких экспериментах хорошо выполняется принцип линейности (закон Ламберта-Бера). В системе имеются два вещества A и B, с профилями элюции cA(t) и cB(t). Тогда спектр смеси
x = cA∙sA+ cB∙sB,
где sA и sB – спектры чистых веществ.
Для моделирования профилей элюции веществ A и B использовались перекрывающиеся гауссовы пики, вычисленные для 30 времен удерживания t =0, 1, 2, …, 30. Они показаны на Рис. 1. Чистые спектры веществ A и B приведены на Рис. 2. Они были рассчитаны для 28 длин волн как сложное наложение нескольких гауссовых пиков.
Смешанные данные X вычислялись по формуле (1) с относительной ошибкой 3%.
Анализ полученных данных методом главных компонент должен проводиться без центрирования и нормировки. Это общее правило для задач MCR.
Зависимости первых двух счетов t1 и t2 от времени приведены на Рис. 9 (левый график).
Рис.9 Результаты анализа данных PCA
Для наглядности там же показаны и концентрационные профили C веществ A и B. Графики для первых двух нагрузок P (вместе с чистыми спектрами S) приведены на Рис. 9 (правая панель).
Можно заметить некоторое сходство в поведении главных компонент и соответствующих исходных данных. Хотя, разумеется, главные компоненты не являются решением задачи MCR, хотя бы по причине их неположительности.
Число главных компонент, конечно, равно 2. Это следствие того, что модельные данные X строились как смесь из двух химических компонентов A и B. Тем не менее, полезно убедится, что метод главных правильно оценивает эту величину.
Рис.10 Определение числа главных компонент
На Рис. 10 (левая панель) приведены графики изменения сингулярных значений σa (SnV, левая ось ординат) и объясненной остаточной дисперсии (ERV, правая ось ординат) в зависимости от числа главных компонент. Видно, что точка PC=2 соответствует перелому на этих кривых. На правой панели Рис. 10 представлены графики нагрузок в зависимости от длины волны, для PC=3 и 4. Сравнивая его с графиком первых нагрузок (Рис. 9), можно заметить, что для старших главных компонент отсутствует какая-нибудь систематика, и они выглядят просто как шум.
Анализ остатков
E=X–TPt
показывает, что относительная среднеквадратичная погрешность моделирования
равна 4%, что примерно соответствует ошибке, добавленной при создании данных.
Для вычисления собственных значений EGV использовалась формула, показанная на Рис. 11.
Рис.11 Вычисление собственных и сингулярных значений на листе Excel
Поясним ее смысл, а также преимущества, которые она доставляет.
Внутренняя функция ScoresPCA(Xdata) вычисляет полную
матрицу счетов T, размерностью 30×28 .К
результату применяется стандартная функция
INDEX(T,,B6), которая
выделяет из матрицы T один столбец с номером, заданным значением в
ячейке B6 – это текущий номер PC. К полученному вектору
ta применяется стандартная
функция
SUMSQ(ta), которая вычисляет сумму
квадратов всех элементов этого вектора, т.е. собственное значение, определенное
формулой (7).
Таким образом, в одной формуле удается скомбинировать несколько последовательных операций. Если выводить все промежуточные результаты на лист, то они займут много места, увеличат файл и замедлят вычисления.
Подробнее эта техника описана здесь.
Полезно изобразить зависимость между первыми счетами, так как это сделано на Рис. 12 (левая панель). У каждой точки показано соответствующее значение времени.
Рис.12 График HELP
Видно, что процесс выходит из начала координат, и в него же и возвращается. Первые 4 точки лежат на прямой линии (красная), начинающейся в точке (0, 0). Они соответствуют начальной стадии, когда выходит только вещество A, а компонент B пока отсутствует. Последние точки (18-30) также лежат на прямой, выделенной голубым цветом. Они соответствуют финальной стадии выхода чистого вещества B, когда вещества A уже нет.
Подобные графики носят название HELP (Heuristic Evolving Latent Projections). Они могут помочь в решении задач MCR, для случая двух или трех компонент. При анализе графика HELP, нужно руководствоваться следующими простыми правилами
1. линейные участки = чистые компоненты;
2. кривые участки = коэлюция;
3. ближе к началу = меньше интенсивность;
4. число поворотов = число чистых компонент.
Как отмечалось выше, решение задачи MCR не является единственным. Его можно изменить с помощью шкалирующих и вращающих преобразований. Идея прокрустова анализа (Procrustes Analysis) состоит в том, чтобы использовать эту неопределенность для трансформации PCA-решения в MCR-решение.
На первом этапе применим масштабирование. Для этого умножим матрицу счетов T на диагональную матрицу R1=diag{r11, r12}
T1=TR1
Матрицу R1 надо подобрать так, чтобы в результате получился прямой угол между участками чистых компонент на графике HELP (Рис. 13). В Excel это можно сделать с помощью метода .
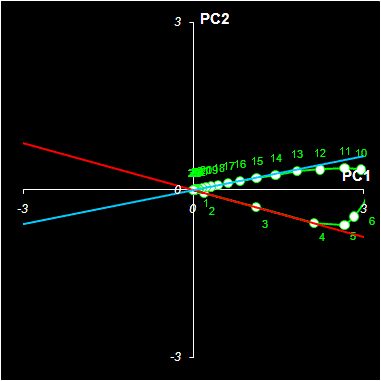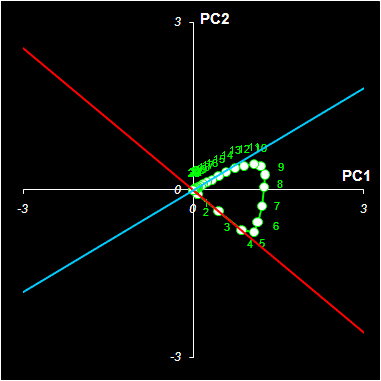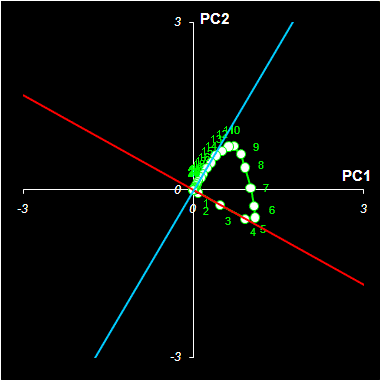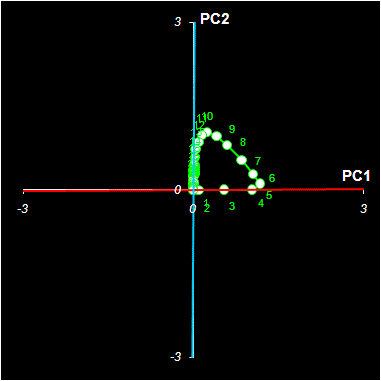
Рис.13 Прокрустов анализ
На втором шаге делается поворот. Для этого новую матрицу T1 нужно умножить на матрицу вращения R2
T2=T1R2
|
где |
|
Угол вращения α надо подобрать так, чтобы прямые, соответствующие чистым компонентам, совпали c направлениями главных осей.
Окончательный результат этих преобразований главных компонент в чистые химические компоненты представлен на Рис. 14.
Рис.14 Решение задачи MCR методом Прокрустова анализа
Оценки концентрационных профилей Chat получены в результате преобразования матрицы PCA-счетов T
Chat=TR1R2=TR, где R=R1R2
Оценку чистых спектров Shat можно теперь найти из нагрузок P по следующей формуле
Shat=P(Rt)–1
Представленные графики свидетельствуют, что задача MCR решена с приемлемой точностью. Анализ остатков
E=X–Chat(Shat)t
показывает, что относительная среднеквадратичная погрешность моделирования (10) равна 4%, т.е. совпадает с точностью, достигнутой в разложении по главным компонентам. Это свидетельствует о том, что найденное решение задачи MCR является эффективным и ничего точнее найти уже нельзя.
При этом найденные концентрационные профили Chat, и спектры Shat не точно совпадают с соответствующими исходными кривыми Ctrue и Strue. Относительная ошибка их определения достигает 19%. Причина этого – масштабная неоднозначность. В нашем случае она возникает на первом шаге прокрустового преобразования – при подгонке одного из двух элементов матрицы R1, второй может быть произвольным. На листе Procrustes первый элемент r11 выбран так, чтобы max {tij}=1, а подбирается второй элемент r22. Легко проверить, что при другом выборе r11 общая погрешность δ не изменится, тогда как индивидуальное расхождение в компонентах будет уже другим.
Масштабную неопределенность можно оценить, сравнив покомпонентно величины концентрационных профилей Ctrue и Chat, а также величины чистых спектров Strue и Shat
Рис.15 Покомпонентное сравнение решений (Прокрустов анализ)
Из Рис. 15 видно, оценки концентраций систематически завышены с коэффициентом 1.07 (для A) и 1.12 (для B), тогда как оценки спектров занижены с коэффициентом 0.93 и 0.90. При этом в произведении c(t)s(λ) получаем 0.995 для A и 1.008 для B – значения близкие (с учетом погрешностей в данных) к 1.
В абстрактном факторном анализе, осуществляемым методом главных компонент, совершенно не важно, в каком порядке расположены строчки в матрице данных X. Их можно перемешать, но результат PCA – матрицы счетов T и нагрузок P от этого не изменятся. В тоже время в задачах MCR, порядок, в котором получались экспериментальные данные, весьма важен, и его нужно использовать для нахождения решения.
Главная идея эволюционного факторного анализа (EFA, Evolving factor analysis) состоит в том, что метод главных компонент применяется не ко всей матрице X, а к последовательности ее подматриц. В методе EFA используют две последовательности.
Расширяющаяся последовательность (прямой проход) включает следующие матрицы. Первая состоит из одной – первой (по времени) строки X, вторая – из двух первых строк, третья – из трех строк, и т.д., вплоть до последней матрицы, равной полной матрице X.
Вторая последовательность – это сокращающиеся матрицы (обратный проход). Ее первая матрица – это полная матрица X, во второй удалена первая строка, в третьей – две первые строки, и т.д., вплоть до матрицы, состоящей только из одной последней строки X.
К каждой подматрице из последовательности применяется разложение по методу главных компонент, и определяются соответствующие сингулярные значения (с.з.) σ1,..,σA. (Рис. 16).
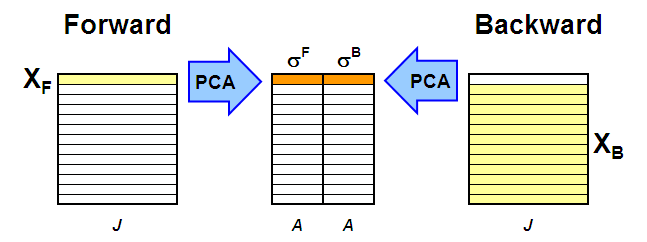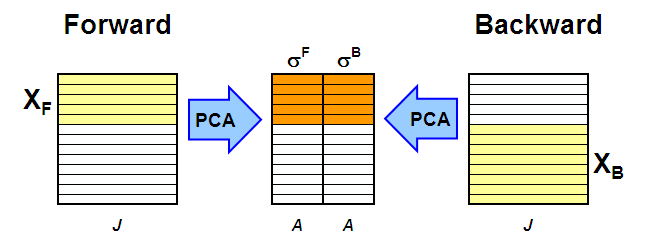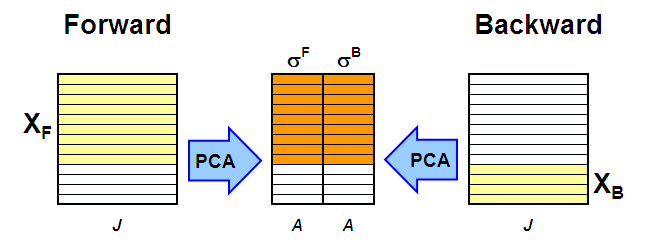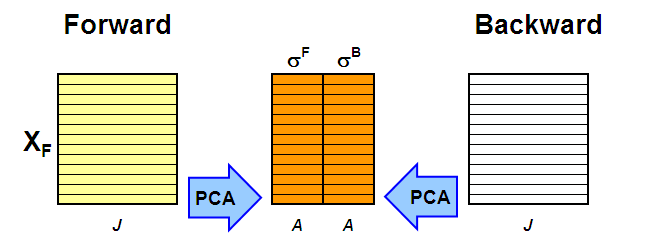
Рис.16 Метод эволюционного факторного анализа
Важнейшая часть метода EFA – это анализ того, как меняются эти с.з. при расширении и сжатии матрицы X.
Рис.17 Изменение сингулярных значений
На Рис. 17 (левая панель) показано, как в нашем примере меняются первое и второе с.з. (левая ось ординат) в прямом проходе. На том же графике приведены и кривые концентрационных профилей веществ A и B (правая ось ординат). Видно, что возрастание с.з. связано с появлением соответствующего вещества в системе. Аналогичный график для обратного прохода (правая панель на Рис. 17) показывает, что уменьшение с.з. связано с уходом вещества из системы. Часто на подобных графиках изображаются логарифмы с.з., для того чтобы уменьшить масштаб их различия.
Анализируя оба графика EFA совместно можно построить оценки концентрационных окон Wa(t) для всех компонентов системы. Это делается по следующему простому алгоритму.
Пусть ε – это некоторая
малая величина, ниже которой с.з. считается незначительным. Для каждой главной
компоненты a=1,…,A рассматривается пара с.з.
![]() . Для первой ГК (a=1) эта пара состоит из первого с.з.
для прямого прохода и последнего (A) с.з. для обратного прохода. Следующая пара (a=2) включает второе с.з из прямого и
предпоследнее с.з. (A–1) из обратного, и т.д.
Тогда,
. Для первой ГК (a=1) эта пара состоит из первого с.з.
для прямого прохода и последнего (A) с.з. для обратного прохода. Следующая пара (a=2) включает второе с.з из прямого и
предпоследнее с.з. (A–1) из обратного, и т.д.
Тогда,
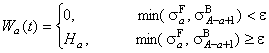
В этом алгоритме предполагается,
что тот химический компонент, который первым появляется, первым и исчезает.
Выбор критического уровня ε проводится с учетом того, как определялось число главных
компонент A в полном PCA. Из Рис. 10 видно, что ε < 1. Мы его
взяли равным 0.05. Высота окна Ha величина произвольная. В частности,
можно положить Ha=A–a+1
или ![]() .
.
Рис.18 Решение задачи MCR методом EFA
Концентрационные окна Wa можно считать грубым приближением соответствующих концентрационных профилей, как это показано на Рис. 18 (левая панель). Тогда оценки чистых спектров Shat можно найти по формуле (5). Они представлены на правой панели Рис. 18.
Видно, что приближение не очень хорошее, что и подтверждает величина δ = 62%, которая значительно хуже, чем в прокрустовом анализе. Однако метод EFA интересен не решением задачи MCR, а тем, что он дает фундамент для других, более точных методов. С этой точки зрения главный результат EFA – это найденные концентрационные окна
На листе EFA используется еще одна сложная формула для вычисления сингулярных значений (Рис. 19). Она похожа на формулу, представленную на Рис. 11, но в ней имеются и свои особенности.
Рис.19 Вычисление сингулярных значений в методе EFA на листе Excel
Внутренняя часть выражения имеет вид OFFSET(Xdata,,,A9). Здесь, с помощью стандартной функции OFFSET, из массива данных X отбирают столько первых строк, сколько заданно значением в ячейке A9 – это текущий номер момента времени ti. В результате получается усеченная матрица, для которой вычисляется матрица счетов, из которой выбирается столбец с номером, заданным в ячейке C$5, и т.д.
Для обратного прохода внутренняя функция имеет вид OFFSET(Xdata,A9-1,,I-A9+1). Здесь опять используется ссылка на ячейку A9. В результате из данных X выбираются I-A9+1 строки, начиная со строки A9-1
На этом примере видно, какой большой выигрыш дает использование подобных сложных, но компактных формул. Если бы мы выводили на лист все промежуточные результаты, то нам потребовалось бы разместить 60 подматриц XF и XB, и 60 матриц счетов, только для того, чтобы определить все сингулярные значения.
Идея оконного факторного анализа (Windows Factor Analysis, WFA) состоит в последовательном удалении из исходных данных X тех строчек, в которых концентрация каждого химического компонента отлична от нуля. Удаляемые области соответствуют концентрационным окнам, определяемым с помощью EFA. Оставшуюся после удаления матрицу Xa разлагают с помощью PCA и определяют матрицу нагрузок Pa. Из-за того, что один химический компонент удален из системы, число главных PCA компонент уменьшается на единицу и становится равным A-1. Матрица Pa несет в себе информацию о спектрах всех химических компонентов, кроме исключенного. Поэтому для того, чтобы определить этот исключенный компонент, надо найти вектор ортогональный к Pa.
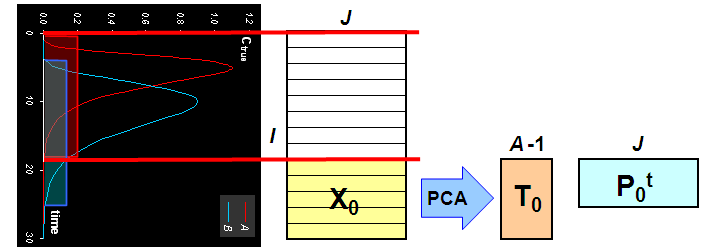
Рис.20 Метод оконного факторного анализа WFA
Алгоритм WFA состоит их следующих шагов, повторяемых для каждого химического компонента a=1,…, A:
1. Определяется матрица Xa
2. К матрице Xa применяется PCA Xa = Ta (Pa)t + Ea , и находится матрица Pa
3. Вычисляется матрица Za=X–XPa(Pa)t
4. К матрице Za применяется PCA: Za = tZ(pZ)t + EZ с одной главной компонентой, и находится вектор счетов tZ
5. Все отрицательные элементы в tZ заменяются нулями, и этот результат является оценкой концентрационного профиля ca для исследуемого компонента
В приведенном алгоритме п.4 заслуживает отдельного комментария. Теоретически матрица Za имеет ранг A–(A–1) = 1, поэтому каждый ее столбец должен быть пропорционален искомому концентрационному профилю ca. Однако, в ходе описанных выше расчетов появляются ошибки, которые изменяют результат. Именно для устранения ошибок и выполняется шаг 4, который, в принципе, можно заменить выбором одного столбца в матрице Za имеющего наибольшую норму.
После того как алгоритм применен к каждому компоненту и определена матрица оценок концентрационных профилей Chat, оценки чистых спектров Shat можно найти по формуле (5).
В рассматриваемом примере имеется два компонента: A и B, поэтому WFA нужно сделать два раза. Для определения вещества A нужно удалить из исходных данных X несколько строчек: например со 2-ой по 13-ую. Для определения вещества B нужно удалить строки, например с 4-ой по 25-ую. Это следует из Рис. 18 .
Рис.21 Решение задачи MCR методом WFA
На Рис. 21. представлены решения задачи MCR, найденные методом WFA. Точность приближение δ= 4%, в точности такая же, как и в Прокрустовом вращении
Для вычисления матрицы (в нашем случае – вектор) нагрузок Pa применяется прием, аналогичный рассмотренным выше (см. Рис. 22). Специальная функция MCutRows(Xdata,$F$3,$F$4-$F$3+1) удаляет из данных все строки, начиная со строки, заданной в ячейке F3, и заканчивая строкой, заданной в ячейке F4 - всего $F$4-$F$3+1 строк Затем для усеченных данных определяются PCA-нагрузки с помощью функции LoadingsPCA
Рис.22 Вычисление нагрузок в методе WFA
Вычисление вектора счетов tZ представлено на Рис. 23.
Рис.23 Вычисление вектора счетов в методе WFA
Итерационный целевой факторный анализ (Iterative Target Transform Factor Analysis, ITTFA) решает задачу MCR, последовательно оптимизируя оценку матрицы концентрационных профилей Chat. Идея метода состоит в том, что исходная оценка матрицы Cin проецируется на подпространство, образованное векторами из матрицы PCA счетов T. Для этого используется матрица нормированных счетов U, совпадающая с матрицей левых собственных векторов в разложении по сингулярным значениям (SVD). Чтобы найти U, надо каждый вектор счетов разделить на соответствующее сингулярное значение
ua = ta/σa
Полученная проекция Cout подправляется с учетом ограничений – положительность, унимодальность, и т.п. Подправленный профиль концентраций опять проецируется на T, и т.д.
Алгоритм ITTFA состоит из следующих шагов:
1. Исходная матрица данных разлагается с помощью PCA X = TPt + E, находится матрица T, а затем матрица нормированных счетов U
2. Выбирается начальное приближение для матрицы концентрационных профилей Cin
3. Матрица Cin проецируется на подпространство, образованное T, и определяется матрица
Cout = UUtCin
4. Матрица Cout подправляется с учетом ограничений, например, если какой-то ее элемент отрицателен, то он заменяется нулем. В результате получается оценка Chat
5. Матрица Cin заменяется матрицей Chat
6. Шаги 3-5 повторяются до сходимости
В этом алгоритме критическим является шаг 2 – выбор начального приближения для матрицы концентрационных профилей. При неудачном выборе алгоритм расходится. Третий шаг алгоритма находит математическое решение задачи MCR – матрицу абстрактных профилей Cout, которая, однако, может противоречить физическим ограничениям. Последующий шаг 4 согласует оценку с этими ограничениями, но выталкивает матрицу Chat из пространства главных компонент. Поэтому все начинается заново, пока найденное решение не будет удовлетворять как математическим, так и физическим требованиям.
После того как определена матрица оценок концентрационных профилей Chat, оценки чистых спектров Shat можно найти по формуле (5).
Рассмотрим, как метод ITTFA используется в нашем примере.
Рис.24 Реализация метода ITTFA
На Рис. 24 показан фрагмент страницы ITTFA. Кнопка Calculate запускает простейший VBA макрос, который копирует содержание области Chat и вставляет значения в область Cin. Эта операция повторяется столько раз, сколько указано в клетке F2. Тем самым реализуется заданное число итераций.
В качестве начального приближения были выбраны игольчатые профили, показанные на Рис. 25..
Рис.25 Начальное приближение для матрицы Cin игольчатыми профилями
Через 20 итераций были получены решения, показанные на Рис. 26..
Рис.26 Решение задачи MCR методом ITTFA
Точность подгонки составила δ= 4%, т.е. метод ITTFA дал ту же точность, что и WFA. Нетрудно проверить, что алгоритм ITTFA будет расходиться, если задать неудачное начальное приближение Cin.
Метод чередующихся наименьших квадратов (Alternating Least-Squares, ALS) – это простой и одновременно очень мощный метод решения зада MCR. В отличие от большинства других методов MCR, ALS не опирается на разложение PCA. Вместо этого он использует принцип наименьших квадратов, последовательно применяя на каждом шагу формулы (4) и (5). Так же как ITTFA, метод ALS является итерационным, но его сходимость значительно лучше.
Алгоритм метода выглядит так.
1. Методом PCA определяется число компонент, а методом EFA – концентрационные окна.
2. Задается начальное приближение для матрицы концентрационных профилей Cin .
3. Матрица Cin подправляется с учетом ограничений: элемент этой матрицы заменяется нулем, если он отрицателен, или если соответствующий элемент концентрационного окна равен нулю. Кроме того, матрицу полезно нормировать так, чтобы ее максимальный элемент был равным 1. В результате получается оценка Chat.
4. С помощью формулы (5) находится оценка матрицы чистых спектров Sin –
Sin= Xt Chat (ChattChat)–1.
5. Матрица Sin подправляется – отрицательные элементы заменяются нулями. Получается матрица Shat.
6. С помощью формулы (4) определяется оценка матрицы концентрационных профилей Cout –
Cout=X Shat (ShattShat)–1.
7. Матрица Cin заменяется матрицей Cout .
8. Шаги 3-7 повторяются до сходимости.
Как видно, главное отличие от метода ITTFA состоит в активном использовании концентрационных окон. Как показывает практика, метод ALS не так критичен к выбору начального значения Cin. В частности, в качестве Cin. можно взять и концентрационное окно, определенное методом EFA.
Применение метода ALS для нашего примера показано на листе ALS. Здесь, также как в ITTFA, используется кнопка Calculate, которая запускает аналогичный VBA макрос, копирующий содержание области Cout в область Cin. Число повторов задается значением в клетке F2.
Концентрационные окна были определены методом EFA для уровня шума 0.05. Они же послужили и в качестве начального значения для матрицы Cin. Алгоритм сходится за 10 итераций к результату, который по точности (δ = 4%) совпадает с другими методами.
Рис.27 Решение задачи MCR методом ALS
Мы рассмотрели некоторые методы, используемые для решения задач разрешения кривых. Эта область хемометрики, как никакая другая, изобилует разнообразными подходами. Поэтому, с неизбежностью, за рамками этого пособия остались многие интересные методы, такие как, например, SIMPLISMA, OPA и другие. Разобраться с тем, как они работают можно самостоятельно, используя это пособие как руководство к действию.
Один из подходов к проблеме MCR, тесно связанный с методом ALS, достоин специального изучения. Это метод, объединяющий в себе формальный хемометрический подход (soft modeling) с содержательным кинетическим описанием процессов (hard modeling). Он рассмотрен в отдельном пособии Кинетическое моделирование спектральных данных.
|
|