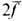),
где a - угол атаки профиля, u - скорость набегающего потока,
а 
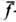-относит.
вогнутость крыла. Коэф. подъёмной силы при этом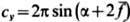 
. Если a и 
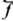-величины
малые, то приближённо су = 2p(a+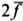
) т. е. cy пропорц. a и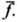 
Чаплыгина - Жуковского постулат - положение, согласно к-рому при безотрывном обтекании профиля крыла потоком идеальной жидкости
или газаточкой плавного схода струй с его контура является хвостовая точка профиля.
При этом предполагается, что хвостовая точка есть точка заострения. Если бы
при безотрывном обтекании профиля идеальной жидкостью струи сходили с его контура
не в хвостовой точке, а в к--л. другой, то в угл. точке или точке заострения
на хвостике скорость была бы бесконечно большой, что физически невозможно. Это
обстоятельство можно рассматривать как обоснова-ние Чаплыгина - Жуковского постулата: постулат является
условием того, чтобы при обтекании профиля с одной острой кромкой скорость во
всех точках была конечной.
Применив Чаплыгина - Жуковского постулат к вычислению циркуляции скорости
Г, можно затем определить подъёмную силу на едини-цу размаха крыла. В случае
тонкого изогнутого профиля G = pusin(a+),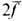
где a - угол атаки профиля, u - скорость набегающего потока,
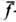а -относит.
вогнутость крыла. Коэф. подъёмной силы при этом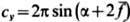
. Если a и 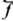-величины
малые, то приближённо су = 2p(a+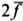) т. е. cy пропорц. a и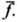
Опыты показывают, что ф-лы для Г и сy
соответствуют действительности лишь приближённо и только при малых значениях
a и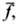 
когда обтекание может быть безотрывным. Наличие вязкости жидкости и образование
на поверхности крылового профиля пограничного слоя несколько (на 10-15%) уменьшают
теоретич. коэф., к-рые, кроме того, зависят ещё от Рейнольдса числа. Если,
напр., a больше нек-рого определённого
для данного профиля и условий обтеканий значения (т. н. критического aкр),
то точка схода струй будет находиться не в хвостовой точке профиля, а в точке
на верх. части контура. Обтекание при этом сопровождается отрывом струй и образованием
вихрей над верх. частью.
|
|
 |
