Глоссарий по физике

Хаос

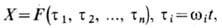
Хаос - сложное, нерегулярное (апериодическое) изменение состояния физ. системы в пространстве и/или во времени.

Происхождение хаотического поведения может быть обусловлено разл. причинами.

X. может представлять собой нек-рое многопериодическое движение:

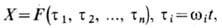
где F-2p-периодическая функция по каждому аргументу. Тогда если среди частот w_i есть несоизмеримые, то реализация представляет сложное изменение со временем вектора состояния X. С возникновением многопериодических движений связан сценарий появления турбулентности по Хопфу. В фазовом пространстве n-периодиче-ское движение описывается траекторией, наматывающейся на n-мерный тор. В частном случае n-торы образуются в результате сложения (суперпозиции) конечного числа гармонических колебаний. Напр., автономная система двух связанных осцилляторов, описываемая ур-ниями

совершает двухпериодическое движение:

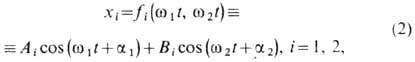
где А₁= А₂, В₁=-В₂, w²₁= w² - k², w²₂= w² + k², a₁ a₂-нач. фазы. Если частоты w₁ и w₂ действительные и несоизмеримые, то соответствующее движение в общем случае апериодическое.

Сложная динамика может возникать также за счёт того, что под действием внеш. факторов параметры системы меняются со временем. Примером является неавтономная система, описываемая у р а в н е н и е м М а т ь ё:

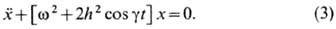
В областях стабильности (за исключением дискретного множества точек) величина х ограничена и меняется апериодически. В соответствии с теоремой Флоке - Ляпунова (иногда называемой Блоха теоремой)эта величина является двухпериодической функцией.

X. возникает, если в системе протекают случайные процессы. Такие процессы могут быть связаны со случайными внеш. воздействиями, а также с флуктуациями внутр. параметров. Примером случайного, хаотического процесса является броуновское движение. Динамика случайных процессов описывается ур-ниями для физ. характеристик - координат, скоростей и др., включающими случайные параметры (ур-ниями Ланжевена), а также ур-ниями для вероятностных характеристик системы. Напр., если процесс марковский, то при определ. допущениях эволюция функции распределения f случайной величины и определяется из ур-ния Фоккера- Планка - Колмогорова:

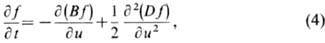
в к-ром В и D - интегральные моменты вероятности перехода системы между разл. допустимыми состояниями.

Случайный процесс характеризуется такими параметрами, как среднее, дисперсия, корреляц. функция, спектральная функция. Важным признаком случайности процесса является убывание корреляций по мере увеличения интервала времени между сопоставляемыми наблюдениями:

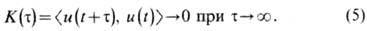
Этому условию не удовлетворяют, вообще говоря, многопериодические движения, подобные тем, к-рые описываются ур-ниями (1), (3). Кроме того, спектральный анализ таких движений выявляет наличие лишь конечного числа несоизмеримых частот и/или счётного (или конечного) чис-ла кратных частот. Поэтому многопериодические движения и колебания линейных неавтономных систем (если, конечно, внеш. "силы" не меняются стохастически) не обладают необходимыми свойствами истинно стохастических колебаний и по отношению к ним термины "хаотический" и "стохастический" употребляются редко.

Сложное поведение, обладающее основными свойствами случайного процесса, обнаруживается у мн. нелинейных динамических систем (т. н. хаос динамический ).Качественно происхождение X. в таких системах связывают с тем, что нелинейные системы можно рассматривать как совокупность неск. взаимодействующих подсистем, обладающих разл. динамическими свойствами. Хаотическая динамика возникает в результате разл. рода процессов синхронизации колебаний указанных подсистем.

Наконец, в квантовых системах, описываемых линейным ур-нием Шрёдингера, стохастические колебания, вообще говоря, невозможны. Однако если характерные времена переходных процессов велики, может наблюдаться явление квантового X. Возможность подобного режима легко понять из того, что в классическом пределе система будет описываться нелинейными ур-ниями движения, для к-рых такая динамика известна (см. выше).

Литература по

1. Заславский Г. М., Стохастичность динамических систем, М., 1984; Рабинович М. И., Трубецков Д. И., Введение в теорию колебаний и волн, 2 изд., М., 1992; Гардинер К. В., Стохастические методы в естественных науках, пер. с англ., М., 1986; Неймарк Ю. И., Ланда П. С., Стохастические и хаотические колебания, М., 1987. Н. А. Кириченко.
   к библиотеке   к оглавлению   FAQ по эфирной физике   ТОЭЭ   ТЭЦ   ТПОИ   ТИ  
   
   
   Знаете ли Вы, в чем ложность понятия "физический вакуум"?

   Физический вакуум - понятие релятивистской квантовой физики, под ним там понимают низшее (основное) энергетическое состояние квантованного поля, обладающее нулевыми импульсом, моментом импульса и другими квантовыми числами. Физическим вакуумом релятивистские теоретики называют полностью лишённое вещества пространство, заполненное неизмеряемым, а значит, лишь воображаемым полем. Такое состояние по мнению релятивистов не является абсолютной пустотой, но пространством, заполненным некими фантомными (виртуальными) частицами. Релятивистская квантовая теория поля утверждает, что, в согласии с принципом неопределённости Гейзенберга, в физическом вакууме постоянно рождаются и исчезают виртуальные, то есть кажущиеся (кому кажущиеся?), частицы: происходят так называемые нулевые колебания полей. Виртуальные частицы физического вакуума, а следовательно, он сам, по определению не имеют системы отсчета, так как в противном случае нарушался бы принцип относительности Эйнштейна, на котором основывается теория относительности (то есть стала бы возможной абсолютная система измерения с отсчетом от частиц физического вакуума, что в свою очередь однозначно опровергло бы принцип относительности, на котором постороена СТО). Таким образом, физический вакуум и его частицы не есть элементы физического мира, но лишь элементы теории относительности, которые существуют не в реальном мире, но лишь в релятивистских формулах, нарушая при этом принцип причинности (возникают и исчезают беспричинно), принцип объективности (виртуальные частицы можно считать в зависимсоти от желания теоретика либо существующими, либо не существующими), принцип фактической измеримости (не наблюдаемы, не имеют своей ИСО).

   Когда тот или иной физик использует понятие "физический вакуум", он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.

   Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик Анри Пуанкаре, уже нельзя. Слишком много фактов противоречит этому.

   Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование "моря" двух компенсирующих друг друга энергий в вакууме - положительной и отрицательной, а также "моря" компенсирующих друг друга частиц - виртуальных (то есть кажущихся) электронов и позитронов в вакууме.

   Однако такая постановка является внутренне противоречивой (виртуальные частицы ненаблюдаемы и их по произволу можно считать в одном случае отсутствующими, а в другом - присутствующими) и противоречащей релятивизму (то есть отрицанию эфира, так как при наличии таких частиц в вакууме релятивизм уже просто невозможен). Подробнее читайте в FAQ по эфирной физике.

   НОВОСТИ ФОРУМА Рыцари теории эфира

   10.11.2021 - 12:37: ПЕРСОНАЛИИ - Personalias -> WHO IS WHO - КТО ЕСТЬ КТО - Карим_Хайдаров. 10.11.2021 - 12:36: СОВЕСТЬ - Conscience -> РАСЧЕЛОВЕЧИВАНИЕ ЧЕЛОВЕКА. КОМУ ЭТО НАДО? - Карим_Хайдаров. 10.11.2021 - 12:36: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от д.м.н. Александра Алексеевича Редько - Карим_Хайдаров. 10.11.2021 - 12:35: ЭКОЛОГИЯ - Ecology -> Биологическая безопасность населения - Карим_Хайдаров. 10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> Проблема государственного терроризма - Карим_Хайдаров. 10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> ПРАВОСУДИЯ.НЕТ - Карим_Хайдаров. 10.11.2021 - 12:34: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вадима Глогера, США - Карим_Хайдаров. 10.11.2021 - 09:18: НОВЫЕ ТЕХНОЛОГИИ - New Technologies -> Волновая генетика Петра Гаряева, 5G-контроль и управление - Карим_Хайдаров. 10.11.2021 - 09:18: ЭКОЛОГИЯ - Ecology -> ЭКОЛОГИЯ ДЛЯ ВСЕХ - Карим_Хайдаров. 10.11.2021 - 09:16: ЭКОЛОГИЯ - Ecology -> ПРОБЛЕМЫ МЕДИЦИНЫ - Карим_Хайдаров. 10.11.2021 - 09:15: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Екатерины Коваленко - Карим_Хайдаров. 10.11.2021 - 09:13: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вильгельма Варкентина - Карим_Хайдаров.