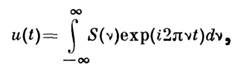
Cпектрометрия оптическая (от спектр и греч. metres - измеряю) - совокупность методов и теория измерений спектров эл--магн. излучения и изучение спектральных свойств веществ и тел в оптич. диапазоне длин волн (~1 нм - 1 мм). Измерения в С. осуществляются с помощью спектральных приборов. Осн. задачи С.: теория спектральных приборов, модельное рассмотрение условий измерений в типовых вариантах, разработка критериев сравнения приборов, способов оптимизации условий и режимов измерений с целью получения наиб. точных результатов за наим. время.
Теоретические основы спектрометрии. Оптич. сигнал u(t)во
времени t может быть представлен преобразованием Фурье в виде линейной
комбинации гармонич. сигналов с частотами v:
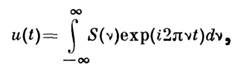
где
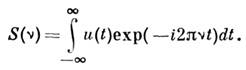
При таком рассмотрении измерение спектра сводится к нахождению амплитуд
и фаз комплексной функции S(v), описывающей спектр сигнала u(t). Реальные
возможности измерений связаны с рядом ограничений и альтернатив. Во-первых,
приёмники излучения реагируют не на интенсивность излучения, а на поток,
пропорциональный произведению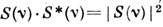 . Во-вторых, в обычной (не лазерной) и. излучение чаще всего некогерентно,
т. к. испускается большим числом элементарных излучателей со случайными
амплитудами и фазами (об особенностях С. когерентного излучения см. в ст.
Лазер,
Лазерная спектроскопия). Поэтому u(t) - случайная функция и, следовательно,
S(v) - случайная величина. Для детерминиров. описания случайного процесса
излучения рассматривают спектр его мощности:
. Во-вторых, в обычной (не лазерной) и. излучение чаще всего некогерентно,
т. к. испускается большим числом элементарных излучателей со случайными
амплитудами и фазами (об особенностях С. когерентного излучения см. в ст.
Лазер,
Лазерная спектроскопия). Поэтому u(t) - случайная функция и, следовательно,
S(v) - случайная величина. Для детерминиров. описания случайного процесса
излучения рассматривают спектр его мощности:
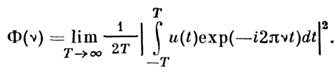
Именно такой спектр измеряют с помощью реальных приёмников. Обратным
преобразованием Фурье от Ф(v) является автокорреляц. функция сигнала u(t):
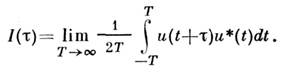
функции Ф(v)и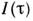 связаны между собой преобразованиями Фурье:
связаны между собой преобразованиями Фурье:
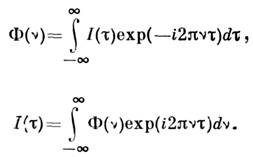
Т. о., исходный процесс u(t)может быть описан любой из функций
Ф(v) и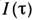 ,
несущих в разной форме одно и то же кол-во информации. В связи с этим возможны
два типа измерит. систем в С.
,
несущих в разной форме одно и то же кол-во информации. В связи с этим возможны
два типа измерит. систем в С.
В приборах, измеряющих непосредственно спектр Ф(v), излучение направляется
на устройство, обладающее свойством спектральной селективности [выделяет
узкий интервал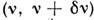 ], и приёмник регистрирует мощность выделенной спектральной составляющей
излучения. Полный спектр Ф(v)получается или последоват. перестройкой
частоты - сканированием (одноканальные системы), или одновременным независимым
приёмом излучения от мн. интервалов
], и приёмник регистрирует мощность выделенной спектральной составляющей
излучения. Полный спектр Ф(v)получается или последоват. перестройкой
частоты - сканированием (одноканальные системы), или одновременным независимым
приёмом излучения от мн. интервалов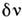 (многоканальные системы).
(многоканальные системы).
Во втором варианте С. в процесс распространения излучения вводится переменная
временная задержка т и измеряется автокорреляц. функция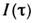 .
наиб. эффективно это реализуется в двухлучевом интерферометре Майкельсона сканированием
по разности хода
.
наиб. эффективно это реализуется в двухлучевом интерферометре Майкельсона сканированием
по разности хода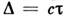 Изменения
сигнала приёмника при таком сканировании дают интерферограмму
Изменения
сигнала приёмника при таком сканировании дают интерферограмму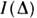 , фурье-образ к-рой представляет собой спектр
, фурье-образ к-рой представляет собой спектр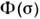 ,
где
,
где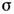 - волновое
число (
- волновое
число ( ,
,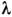 - длина волны). [Подробнее см. в ст. Фурье-спектрометр .Ниже рассматриваются
методы измерения Ф(v).]
- длина волны). [Подробнее см. в ст. Фурье-спектрометр .Ниже рассматриваются
методы измерения Ф(v).]
Инструментальный контур. Модельные описания процессов измерений
в С. основываются на представлениях теории линейных систем. Спектральный
прибор воздействует на измеряемый спектр - входной сигнал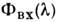 , поэтому наблюдаемый спектр
, поэтому наблюдаемый спектр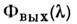 описывается в общем виде интегралом
описывается в общем виде интегралом
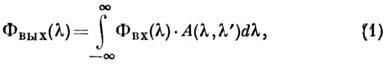
где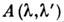 - аппаратная функция (АФ), или инструментальный контур, - индивидуальная
характеристика измерит. прибора, зависящая от двух переменных:
- аппаратная функция (АФ), или инструментальный контур, - индивидуальная
характеристика измерит. прибора, зависящая от двух переменных: - физ. длины волны входящего излучения и
- физ. длины волны входящего излучения и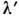 - приборной координаты, напр. спектральной шкалы прибора, по к-рой считывается
отклик прибора, т. е. функция
- приборной координаты, напр. спектральной шкалы прибора, по к-рой считывается
отклик прибора, т. е. функция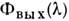
Спектральные приборы чаще всего сочетают оптич. систему (формирующую оптич. сигнал на приёмнике, преобразующем его в электрич. сигнал) с приёмно-регистрирующей системой, на к-рую поступает электрич. сигнал. Соответственно общая характеристика прибора А распадается на оптическую и электрическую АФ. Рассмотрим оптич. часть АФ.
Соотношение (1) позволяет указать способ определения контура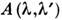 . Пусть входной сигнал представляет собой монохроматич. волну
. Пусть входной сигнал представляет собой монохроматич. волну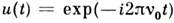 ,
спектр к-рой бесконечно узкая спектральная линия - дельта-функция
,
спектр к-рой бесконечно узкая спектральная линия - дельта-функция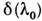 .
Тогда
.
Тогда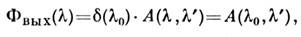 т. е. АФ есть отклик линейного прибора на
т. е. АФ есть отклик линейного прибора на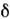 -воздействие.
Для спектральных приборов на основе монохроматоров такая ситуация реализуется
при освещении входной щели излучением изолированной спектральной линии
с шириной bл, много меньшей спектральной ширины щелей монохроматора.
На спектрограмме линия с длиной волны
-воздействие.
Для спектральных приборов на основе монохроматоров такая ситуация реализуется
при освещении входной щели излучением изолированной спектральной линии
с шириной bл, много меньшей спектральной ширины щелей монохроматора.
На спектрограмме линия с длиной волны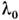 изображается прибором в виде контура колоколообразной формы, максимум к-рого
располагается на делении шкалы
изображается прибором в виде контура колоколообразной формы, максимум к-рого
располагается на делении шкалы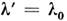 , если шкала точна, или на ином значении
, если шкала точна, или на ином значении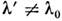 ,
если шкала смещена по к--л. причинам. Ширина этого инструментального контура
соответствует эффективной спектральной ширине щелей sэф (учитывающей
вклады дифракции, аберраций, разъюстировок).
,
если шкала смещена по к--л. причинам. Ширина этого инструментального контура
соответствует эффективной спектральной ширине щелей sэф (учитывающей
вклады дифракции, аберраций, разъюстировок).
Форма измеренного контура может быть различной. При сужении щелей до
размеров дифракц. уширения («нормальные» щели) контур А приближается
к виду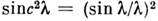 . В другом крайнем случае при достаточно широких щелях контур А приближается
к треугольному; это объясняется тем, что контур А соответствует
изменению сигнала приёмника при сканировании изображения входной щели поперёк
выходной, при этом происходит свёртка двух П-контуров, к-рая и даёт в результате
треугольный контур:
. В другом крайнем случае при достаточно широких щелях контур А приближается
к треугольному; это объясняется тем, что контур А соответствует
изменению сигнала приёмника при сканировании изображения входной щели поперёк
выходной, при этом происходит свёртка двух П-контуров, к-рая и даёт в результате
треугольный контур: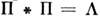 . При промежуточных значениях ширин щелей треугольный контур сглаживается,
что обычно удовлетворительно аппроксимируется гауссовой функцией (если аберрации
не вносят асимметрии). Существенно подчеркнуть, что в рассматриваемом случае
аппаратная функция А имеет ширину sэф в спектральных единицах
(в шкале прибора
. При промежуточных значениях ширин щелей треугольный контур сглаживается,
что обычно удовлетворительно аппроксимируется гауссовой функцией (если аберрации
не вносят асимметрии). Существенно подчеркнуть, что в рассматриваемом случае
аппаратная функция А имеет ширину sэф в спектральных единицах
(в шкале прибора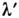 ),
но весь её контур соответствует одной физ. длине волны
),
но весь её контур соответствует одной физ. длине волны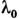 монохроматич. входящего излучения.
монохроматич. входящего излучения.
Если входящее излучение содержит ряд линий в нек-ром диапазоне длин
волн и каждая из них отображается прибором в виде контуров одинаковой формы,
то говорят, что такой прибор обладает свойством спектральной инвариантности
в данном диапазоне. В этом случае функция А зависит только от разности
аргументов; обозначим её: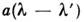 Для такой функции интеграл (1) описывает операцию свёртки:
Для такой функции интеграл (1) описывает операцию свёртки: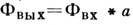 . Допущение об инвариантности является исходным в большинстве теоретич.
работ по С. Но в реальных широкодиапазонных приборах (со сменными дифракц.
решётками) инвариантность в рабочих режимах нередко не соблюдается, что
приходится принимать во внимание при решении обратных задач - восстановления
истинного спектра по измеренному.
. Допущение об инвариантности является исходным в большинстве теоретич.
работ по С. Но в реальных широкодиапазонных приборах (со сменными дифракц.
решётками) инвариантность в рабочих режимах нередко не соблюдается, что
приходится принимать во внимание при решении обратных задач - восстановления
истинного спектра по измеренному.
Для линейчатого спектра на входе вводится характеристика прибора, называемая
разрешением (возможность раздельного наблюдения двух близких линий равной
интенсивности). Разрешение численно равно ширине функции а, т. е. значению
sэф, т. к. при сближении двух линий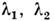 до расстояния
до расстояния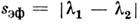 их инструментальные контуры а1 и а2 или
сливаются в трапецеидальный контур (при треугольной форме а), или
разделяются лишь небольшим провалом (при дифракц. форме а; Рэлея критерий ).Отношение
длины волны к разрешению наз. разрешающей способностью:
их инструментальные контуры а1 и а2 или
сливаются в трапецеидальный контур (при треугольной форме а), или
разделяются лишь небольшим провалом (при дифракц. форме а; Рэлея критерий ).Отношение
длины волны к разрешению наз. разрешающей способностью: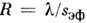 , где
, где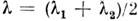 .
.
Кроме отклика на одиночную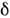 -функцию
на входе важное значение для полноты модельного описания имеет др. предельный
случай, когда входной сигнал обладает сплошным спектром (бесконечная последовательность
-функцию
на входе важное значение для полноты модельного описания имеет др. предельный
случай, когда входной сигнал обладает сплошным спектром (бесконечная последовательность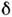 -функций).
Тогда при фиксиров. положении всех оптич. элементов монохроматора (при
остановленном сканировании) в фокальной плоскости образуется континуум
монохроматич. изображений входной щели, последовательно смещённых за счёт
угл. дисперсии. Суперпозиция этой последовательности на выходной щели соответствует
операции свёртки, в результате к-рой формируется выходящий поток. Контур
его спектра, в отличие от АФ, наз. функцией пропускания (ФП). Длина волны,
соответствующая максимуму ФП, наз. длиной волны настройки
-функций).
Тогда при фиксиров. положении всех оптич. элементов монохроматора (при
остановленном сканировании) в фокальной плоскости образуется континуум
монохроматич. изображений входной щели, последовательно смещённых за счёт
угл. дисперсии. Суперпозиция этой последовательности на выходной щели соответствует
операции свёртки, в результате к-рой формируется выходящий поток. Контур
его спектра, в отличие от АФ, наз. функцией пропускания (ФП). Длина волны,
соответствующая максимуму ФП, наз. длиной волны настройки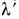 ,
ширина контура ФП наз. выделяемым спектральным интервалом
,
ширина контура ФП наз. выделяемым спектральным интервалом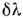 ,
отношение
,
отношение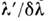 - селективностью С.
- селективностью С.
Зная отклики прибора на два осн. вида тестовых сигналов -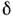 -функцию
и сплошной фон, можно применять интеграл (1) к описанию измерений двух
осн. видов спектров - излучения и поглощения (точнее - пропускания, т.
к. обычно измеряется не поток, поглощённый в веществе, а прошедший или
отражённый поток). Спектр потока
-функцию
и сплошной фон, можно применять интеграл (1) к описанию измерений двух
осн. видов спектров - излучения и поглощения (точнее - пропускания, т.
к. обычно измеряется не поток, поглощённый в веществе, а прошедший или
отражённый поток). Спектр потока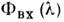 представляется суперпозицией линий или полос, описываемых произведениями
нек-рой пост. величины на нормированную к единице функцию распределения
представляется суперпозицией линий или полос, описываемых произведениями
нек-рой пост. величины на нормированную к единице функцию распределения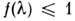 :
:
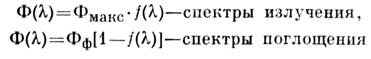
Одиночная полоса в силу особенностей происхождения спектров (см. Спектры
оптические)имеет контур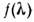 колоколообразной формы, аппроксимируемый в первом приближении Гаусса функцией:
колоколообразной формы, аппроксимируемый в первом приближении Гаусса функцией:
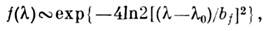
где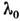 - положение максимума, 6/ - ширина на полувысоте. Воздействие прибора на
- положение максимума, 6/ - ширина на полувысоте. Воздействие прибора на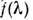 описывается в соответствии с (1) выражением
описывается в соответствии с (1) выражением
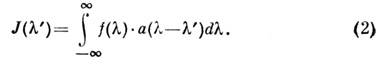
Здесь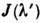 - контур, наблюдаемый на выходе монохроматора в ходе сканирования,
- контур, наблюдаемый на выходе монохроматора в ходе сканирования, - инструментальный контур, обладающий свойством инвариантности. Важно подчеркнуть,
что при измерениях спектров поглощения или широких полос излучения инструментальный
контур а в (2) должен соответствовать ФП и только при измерениях отд. линий
излучения свёртка (2) осуществляется с АФ. Анализ выражения (2) показывает,
что искажающее действие прибора тем больше, чем больше кривизна измеряемого
контура, т. е. чем больше вторая производная
- инструментальный контур, обладающий свойством инвариантности. Важно подчеркнуть,
что при измерениях спектров поглощения или широких полос излучения инструментальный
контур а в (2) должен соответствовать ФП и только при измерениях отд. линий
излучения свёртка (2) осуществляется с АФ. Анализ выражения (2) показывает,
что искажающее действие прибора тем больше, чем больше кривизна измеряемого
контура, т. е. чем больше вторая производная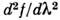 .
Поэтому в качестве количеств. характеристики искажений принимается относит.
уменьшение максимума контура (где вторая производная наибольшая), называемое
щелевой погрешностью
.
Поэтому в качестве количеств. характеристики искажений принимается относит.
уменьшение максимума контура (где вторая производная наибольшая), называемое
щелевой погрешностью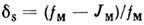 Эта погрешность пропорциональна квадрату отношения ширин контуров f
и а. В гауссовом приближении
Эта погрешность пропорциональна квадрату отношения ширин контуров f
и а. В гауссовом приближении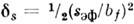 ,
если
,
если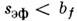 ,
и измерения формы контуров спектров с погрешностью
,
и измерения формы контуров спектров с погрешностью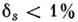 возможны лишь при sэф< bf/7.
возможны лишь при sэф< bf/7.
В реальных приборах всегда имеет место расстояние излучения на оптич. элементах. Кроме того, возможно появление на выходе излучения, проходящего в нерабочих порядках дифракции. Поэтому для целей измерений сплошных (полосатых) спектров описание прибора с помощью контуров АФ и ФП, локализованных только в окрестности длины волны настройки, становится недостаточным. Необходимо учитывать также крылья контуров спектральных л и н и й.
Для каждой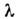 на входе рассматривается контур АФ, записанный во всём рабочем диапазоне
сканирования от начальной
на входе рассматривается контур АФ, записанный во всём рабочем диапазоне
сканирования от начальной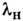 до конечной
до конечной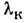 .
В этом контуре, кроме осн. части спектральной линии шириной sэф
в окрестности
.
В этом контуре, кроме осн. части спектральной линии шириной sэф
в окрестности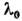 ,
учитываются и протяжённые крылья от фона рассеянного излучения и дополнит.
пики от др. порядков дифракции на делениях шкалы
,
учитываются и протяжённые крылья от фона рассеянного излучения и дополнит.
пики от др. порядков дифракции на делениях шкалы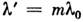 , т = 1, 2, 3... Совокупность таких АФ для всех элементарных компонент
, т = 1, 2, 3... Совокупность таких АФ для всех элементарных компонент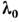 исследуемого сплошного спектра даёт полную картину свойств прибора в его
рабочем диапазоне:
исследуемого сплошного спектра даёт полную картину свойств прибора в его
рабочем диапазоне: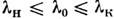 .
Графически эта картина представляется трёхмерной поверхностью
.
Графически эта картина представляется трёхмерной поверхностью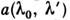 и наз. полной аппаратной функцией (инвариантность в общем случае не предполагается).
и наз. полной аппаратной функцией (инвариантность в общем случае не предполагается).
Аналогичным образом рассматриваются функции пропускания ФП для каждой
длины волны настройки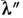 Гл. части контуров ФП в окрестности
Гл. части контуров ФП в окрестности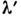 определяют полезный поток на выходе:
определяют полезный поток на выходе: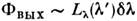 . Здесь
. Здесь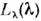 - спектральное распределение спектральной плотности яркости источника,
- спектральное распределение спектральной плотности яркости источника,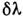 - ширина ФП на
- ширина ФП на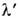 . Интеграл по области крыльев ФП определяет поток мешающего излучения Р посторонних
длин волн. Подчеркнём, что спектр мешающего излучения определяется спектром
входящего потока и может быть существенно шире диапазона
. Интеграл по области крыльев ФП определяет поток мешающего излучения Р посторонних
длин волн. Подчеркнём, что спектр мешающего излучения определяется спектром
входящего потока и может быть существенно шире диапазона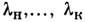 , предусмотренного конструкцией прибора. Отношение потока к полезному потоку
наз. уровнем мешающего излучения: w = Р/Фмакс Эта величина является
важнейшей характеристикой спектральных приборов, нередко лимитирующей точность
измерений.
, предусмотренного конструкцией прибора. Отношение потока к полезному потоку
наз. уровнем мешающего излучения: w = Р/Фмакс Эта величина является
важнейшей характеристикой спектральных приборов, нередко лимитирующей точность
измерений.
Полный набор всех АФ и полный набор всех ФП несут одну и ту же информацию о приборе. В графич. представлении совокупность всех АФ и ФП образует континуумы взаимно перпендикулярных сечений одной и той же трёхмерной полной АФ.
Модельное описание с помощью функций АФ и ФП, изложенное на примере монохроматоров с решётками, применяется также и к др. приборам и методам С. со спектрально-селективной фильтрацией или модуляцией - как одноканальным, так и многоканальным (см. рис. 2 в ст. Спектральные приборы).
При достаточно полном устранении мешающего излучения, пренебрежимых
размерах искажений монохроматич. изображений щели и отсутствии погрешностей
в механизме сканирования можно полагать, что контуры АФ и ФП практически
совпадают, и тогда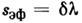 и R = С. В дальнейшем будем полагать, что эти равенства выполняются.
и R = С. В дальнейшем будем полагать, что эти равенства выполняются.
Приёмно-регистрирующие системы и энергетические ограничения. В рамках
оптич. С. обычно предполагается, что источники шумов не столь велики, чтобы
невозможно было корректно ставить задачу измерений формы контуров полосатых
спектров (или хотя бы интегральных интенсивностей в линейчатых спектрах).
Условия измерений характеризуются значениями отношения сигнала к шуму М
= Ф/Фш [Ф - полезный поток, Фш - поток, эквивалентный
шуму приёмно-регистрирующих систем (ПРС)], причём в С. значения М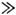 1,
а методами с меньшим значением М решают задачи выделения сигнала
на фоне шумов в общей теории оптико-электронных приборов. Используемые
в С. ПРС разнообразны. Применяются и фотоэлектронные приёмники с уровнем
шума, зависящим от сигнала (фотонный шум), и тепловые приёмники с уровнем
шума, не зависящим от потока и имеющим равномерный частотный спектр (белый
шум); и те и другие могут работать в сочетании с ЭВМ. Универсальных моделей
для всех видов ПРС нет. Рассмотрим, напр., линейную модель типа (2):
1,
а методами с меньшим значением М решают задачи выделения сигнала
на фоне шумов в общей теории оптико-электронных приборов. Используемые
в С. ПРС разнообразны. Применяются и фотоэлектронные приёмники с уровнем
шума, зависящим от сигнала (фотонный шум), и тепловые приёмники с уровнем
шума, не зависящим от потока и имеющим равномерный частотный спектр (белый
шум); и те и другие могут работать в сочетании с ЭВМ. Универсальных моделей
для всех видов ПРС нет. Рассмотрим, напр., линейную модель типа (2):
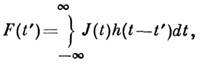
где F(t') - регистрируемый сигнал, J(t) - сигнал приёмника,
воспринимающего изменения потока во времени от сканирующего монохроматора,
h(t
- t')- импульсный отклик ПРС (реакция на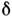 -импульс
на входе), фурье-образ к-рого в пространстве частот,
-импульс
на входе), фурье-образ к-рого в пространстве частот,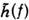 , наз. передаточной функцией. Если в ПРС колебания сигнала невелики и превалирует
инерционное звено (напр., ДС-фильтр шумов с постоянной времени
, наз. передаточной функцией. Если в ПРС колебания сигнала невелики и превалирует
инерционное звено (напр., ДС-фильтр шумов с постоянной времени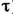 ),
то имеет место простая связь
),
то имеет место простая связь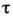 с
охватываемой функцией
с
охватываемой функцией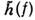 полосой частот
полосой частот , Значениями
, Значениями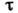 определяются
инерционные искажения контура входного сигнала J, а значениями
определяются
инерционные искажения контура входного сигнала J, а значениями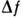 - уровень шумов на выходе.
- уровень шумов на выходе.
Искажения контура J характеризуются инерционной погрешностью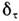 (имеющей аналогично
(имеющей аналогично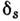 смысл относит. снижения максимума контура). При умеренных скоростях сканирования
(
смысл относит. снижения максимума контура). При умеренных скоростях сканирования
(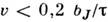 , где bJ - ширина J в единицах спектральной шкалы) имеет место приближённое
выражение
, где bJ - ширина J в единицах спектральной шкалы) имеет место приближённое
выражение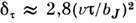 Напр., измерения формы J контуров с погрешностью
Напр., измерения формы J контуров с погрешностью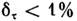 возможны лишь за время bJ/v, превышающее в 17 раз постоянную
времени
возможны лишь за время bJ/v, превышающее в 17 раз постоянную
времени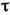 .
.
Инерционные погрешности могут быть уменьшены построением более сложных ПРС высших порядков или переходом к шаговому сканированию с отсчётом и усреднением сигнала на каждом шаге.
Если в системе применён приёмник с плотностью среднеквадратичного белого
шума в единичной полосе частот ФП1[Вт*Гц-1/2] и эта
плотность не зависит от сигнала, то приведённый ко входу уровень шумов
в системе с полосой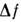 будет
будет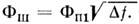 Общее выражение для потока, проходящего через оптич. систему, имеет вид
Общее выражение для потока, проходящего через оптич. систему, имеет вид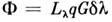 (q - коэф. потерь, G - геометрический фактор системы). Отсюда получается
выражение для отношения сигнала к шуму, М=Ф/ФШ, и находятся
общие энергетич. условия, определяющие диапазоны возможностей измерит.
систем рассматриваемого типа: для случая измерений полосатых спектров излучения
и поглощения
(q - коэф. потерь, G - геометрический фактор системы). Отсюда получается
выражение для отношения сигнала к шуму, М=Ф/ФШ, и находятся
общие энергетич. условия, определяющие диапазоны возможностей измерит.
систем рассматриваемого типа: для случая измерений полосатых спектров излучения
и поглощения
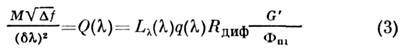
(G' - вертикальная составляющая геом. фактора приёмника); для случая
измерений линейчатых спектров излучения
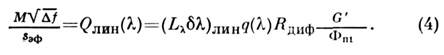
Левая часть равенства (3) соответствует определению энергетического
фактора Q как отношения сигнал/шум при единичной полосе частот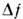 и единичном выделяемом спектральном интервале
и единичном выделяемом спектральном интервале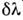 Наряду с Q пользуются также фактором качества К, значения
к-рого не зависят от выбора спектральной шкалы. Он получается из Q заменой
Наряду с Q пользуются также фактором качества К, значения
к-рого не зависят от выбора спектральной шкалы. Он получается из Q заменой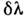 на
на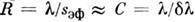 :
:
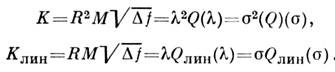
Величины Q, К характеризуют качество прибора. Чем больше Q и К, тем больше могут быть возможности измерений по разрешающей способности
ft, отношению сигнал/шум М и быстродействию (т. к. чем больше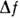 , тем меньше постоянная времени фильтра
, тем меньше постоянная времени фильтра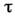 ,
меньше инерционность и больше может быть скорость измерений). Правые части
в соотношениях (3) и (4) показывают, от каких конструктивных параметров
зависит качество прибора. Здесь видно, что вклад оптич. части прибора определяется
только двумя величинами (если она согласована с источником и приёмником
но геом. фактору) - коэф. потерь q и дифракц. пределом Rдиф
= mNL (т - порядок спектра; N, L - частота штрихов и ширина
решётки), а вклады источника и приёмника - яркостью, плотностью шума и
величиной G', согласованной с параметрами монохроматора: G' = hH/L, где
h, Н - высоты щели и эшелотта.
,
меньше инерционность и больше может быть скорость измерений). Правые части
в соотношениях (3) и (4) показывают, от каких конструктивных параметров
зависит качество прибора. Здесь видно, что вклад оптич. части прибора определяется
только двумя величинами (если она согласована с источником и приёмником
но геом. фактору) - коэф. потерь q и дифракц. пределом Rдиф
= mNL (т - порядок спектра; N, L - частота штрихов и ширина
решётки), а вклады источника и приёмника - яркостью, плотностью шума и
величиной G', согласованной с параметрами монохроматора: G' = hH/L, где
h, Н - высоты щели и эшелотта.
Системы равного качества (в смысле Q, К)могут быть реализованы в трёх основных конструктивных направлениях:
1. Максимум R - построение приборов высокой разрешающей способности
(до 106) с большими решётками, работающих медленно (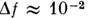 Гц, постоянная времени
Гц, постоянная времени -
до десятков секунд) при небольших значениях М.
-
до десятков секунд) при небольших значениях М.
2. Максимум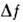 - построение приборов скоростной С. с устройствами быстрого сканирования
и регистрации (до
- построение приборов скоростной С. с устройствами быстрого сканирования
и регистрации (до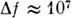 Гц,
Гц,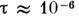 с)
при снижении R до 30-100.
с)
при снижении R до 30-100.
3. Максимум М (до 105 при соответствующем диапазоне
линейности) - построение приборов для прецизионных измерений контуров спектров
при умеренных R и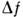 (см. Спектрофотометрия).
(см. Спектрофотометрия).
С помощью критериев Q или К оцениваются в С. возможности
и др. типов систем. При этом могут изменяться показатели степени у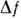 или R (напр., R3 в фурье-спектрометрах)либо
или R (напр., R3 в фурье-спектрометрах)либо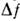 может оказаться нерегулируемой константой, тогда параметр
может оказаться нерегулируемой константой, тогда параметр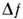 переходит в правую часть соотношений (3) и (4) и т. д. Вводятся также дополнит.
параметры, характеризующие спектральную или пространственную многоканальность,
квантовый выход, характер шумов, протяжённость регистрируемых диапазонов,
полное время измерений и т. п.
переходит в правую часть соотношений (3) и (4) и т. д. Вводятся также дополнит.
параметры, характеризующие спектральную или пространственную многоканальность,
квантовый выход, характер шумов, протяжённость регистрируемых диапазонов,
полное время измерений и т. п.
Оптимальные режимы, редукция. Общим свойством спектрометрич.
систем является альтернативное соотношение между систематическими и случайными
погрешностями (шумами). Напр., в монохроматорах при уменьшении ширины щелей
sэф
систематич. погрешности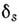 убывают пропорц. , но одновременно с такой же скоростью падает поток
убывают пропорц. , но одновременно с такой же скоростью падает поток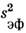 (сигнал) и возрастает относит. уровень шумов - случайная погрешность
(сигнал) и возрастает относит. уровень шумов - случайная погрешность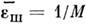 . При увеличении sэф, напротив, растут систематич.
. При увеличении sэф, напротив, растут систематич.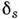 ,
но убывают случайные погрешности
,
но убывают случайные погрешности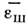 В благоприятных ситуациях (гладкие спектры, «мощный» прибор в смысле Q)может
существовать диапазон значений sэф, где обе погрешности
пренебрежимы, но нередко такой диапазон отсутствует и возникает задача
поиска оптим. значения
В благоприятных ситуациях (гладкие спектры, «мощный» прибор в смысле Q)может
существовать диапазон значений sэф, где обе погрешности
пренебрежимы, но нередко такой диапазон отсутствует и возникает задача
поиска оптим. значения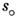 по подходящему критерию. Выбор критерия зависит от того, будет ли применяться
редукция данных (методы решения обратных задач С.- нахождение истинного
контура спектра по наблюдаемому).
по подходящему критерию. Выбор критерия зависит от того, будет ли применяться
редукция данных (методы решения обратных задач С.- нахождение истинного
контура спектра по наблюдаемому).
Редукция прежде всего требует хорошего знания полной АФ прибора. Напр.,
если измерения описываются свёрткой типа (2): J = f * а, то для
фурье-образов имеет место равенство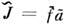 , и если а известна точно, а J не содержит шумов, то редукция эффективно
осуществляется делением фурье-обраяов:
, и если а известна точно, а J не содержит шумов, то редукция эффективно
осуществляется делением фурье-обраяов: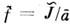 .
Наложение шумов или неполнота знания а резко ограничивают возможности редукции.
.
Наложение шумов или неполнота знания а резко ограничивают возможности редукции.
Если результаты измерений предполагается использовать непосредственно
(без редукции), то подходящим критерием оптимума является общее требование
минимума погрешностей, что формально сводится к отысканию таких значений
регулируемых параметров (ширин оптической и электрической АФ), при к-рых
сумма систематических (щелевой и инерционной) и случайной погрешностей
минимальна. Характер взаимосвязей в оптим. режиме можно выразить следующим
образом:
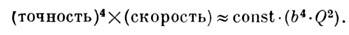
Здесь точностью названа величина, обратная суммарной погрешности, а
скоростью - величина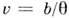 , где
, где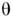 - время
регистрации полосы шириной Ь. Существенно, что точность и скорость
находятся в альтернативном соотношении, показатель степени точности (4)
определяет, насколько она критична, а показатели степени у параметров b и
Q, от к-рых зависит константа справа, показывают, что структурность
измеряемого спектра влияет на точность и производительность измерений сильнее,
чем «мощность» спектрометра.
- время
регистрации полосы шириной Ь. Существенно, что точность и скорость
находятся в альтернативном соотношении, показатель степени точности (4)
определяет, насколько она критична, а показатели степени у параметров b и
Q, от к-рых зависит константа справа, показывают, что структурность
измеряемого спектра влияет на точность и производительность измерений сильнее,
чем «мощность» спектрометра.

В. А. Никитин
|
|