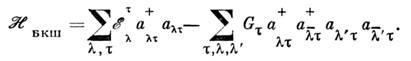
Сверхтекучая модель ядра - обобщение одночастичной оболоченной модели ядра, учитывающее парные корреляции нуклонов вблизи поверхности Ферми в средних и тяжёлых ядрах. Сверхтекучая модель ядра опирается на понятие остаточного взаимодействия нуклонов. Согласно модели оболочек, значит. часть реального нуклон-нуклонного взаимодействия может быть учтена с помощью введения среднего, самосогласованного поля ядра, в к-ром нейтроны и протоны движутся почти независимо. Неучтённая часть нуклон-нуклонного взаимодействия- т. н. остаточное взаимодействие - чрезвычайно важна для понимания мн. свойств ядра. Если остаточное взаимодействие имеет характер притяжения, то оно существеннейшим образом изменяет движение нуклонов вблизи поверхности Ферми, придавая ему коррелированный характер. Для двух взаимодействующих частиц с противоположными импульсами и направлениями спинов, находящихся у поверхности Ферми, принцип Паули ограничивает возможное взаимодействие. В результате оказывается, что трёхмерный потенциал для пары частиц у поверхности Ферми даже при малом притяжении приводит к связанному состоянию.
В наиболее распространённых вариантах сверхтекучая модель ядра используется матем. аппарат теории сверхпроводимости (см. Сверхтекучесть атомных ядер ). Теория сверхтекучей модели ядра разработана независимо С. Т. Беляевым, А. Б. Мигдалом и В. Г. Соловьёвым. При этом в основе лежал либо метод Боголюбова канонических преобразований, либо ур-ния Л. П. Горькова в методе Грина функций.
В сверхтекучей модели ядра используется гамильтониан Бардина - Купера - Шриффера (БКШ).
Применительно к ядру он имеет вид:
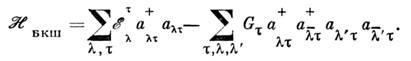
Здесь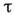 = n, р - т. н. изотоп и ч. индекс (п - нейтроны, р - протоны),
= n, р - т. н. изотоп и ч. индекс (п - нейтроны, р - протоны),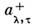 ,
,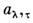 - операторы рождения и уничтожения нуклона сорта
- операторы рождения и уничтожения нуклона сорта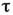 в состоянии
в состоянии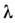 с энергией
с энергией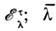 - состояние, отличающееся от
- состояние, отличающееся от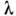 знаком угл. момента нуклона; Gnp - константа парного взаимодействия
нейтронов или протонов. Знак второго слагаемого выбран так, что притяжению
нуклонов отвечает G > 0. Гамильтониан не содержит взаимодействий
нейтронов с протонами, эти подсистемы выступают в сверхтекучей модели ядра как независимые.
Поэтому в дальнейшем рассматриваем нейтроны (для протонов результаты аналогичны).
знаком угл. момента нуклона; Gnp - константа парного взаимодействия
нейтронов или протонов. Знак второго слагаемого выбран так, что притяжению
нуклонов отвечает G > 0. Гамильтониан не содержит взаимодействий
нейтронов с протонами, эти подсистемы выступают в сверхтекучей модели ядра как независимые.
Поэтому в дальнейшем рассматриваем нейтроны (для протонов результаты аналогичны).
Гамильтониан (1) приближённо диагонализуется с помощью линейного канонич.
преобразования Боголюбова:
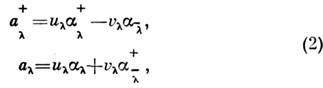
где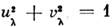 . Это преобразование трансформирует взаимодействующие частицы в невзаимодействующие
квазичастицы, представляющие собой суперпозицию нейтрона (протона) и нейтронной
(протонной) дырки. Т. к. операторы рождения и уничтожения квазичастиц являются
линейными комбинациями аналогичных операторов частиц, то гамильтониан,
диагональный в терминах квазичастиц, будет нарушать закон сохранения числа
частиц. Для приближённого исправления этого дефекта переходят от (1) к
вспомогат. гамильтониану
. Это преобразование трансформирует взаимодействующие частицы в невзаимодействующие
квазичастицы, представляющие собой суперпозицию нейтрона (протона) и нейтронной
(протонной) дырки. Т. к. операторы рождения и уничтожения квазичастиц являются
линейными комбинациями аналогичных операторов частиц, то гамильтониан,
диагональный в терминах квазичастиц, будет нарушать закон сохранения числа
частиц. Для приближённого исправления этого дефекта переходят от (1) к
вспомогат. гамильтониану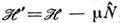 , где
, где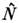 - оператор числа частиц, а
- оператор числа частиц, а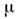 -
множитель Лагранжа, имеющий смысл химического потенциала. Он определяется
из условия
-
множитель Лагранжа, имеющий смысл химического потенциала. Он определяется
из условия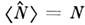 ,
где N - число частиц данного сорта.
,
где N - число частиц данного сорта.
Для приведения гамильтониана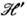 к диагональному виду необходимо коэф. преобразования в ф-ле (2) выбрать
в виде:
к диагональному виду необходимо коэф. преобразования в ф-ле (2) выбрать
в виде:
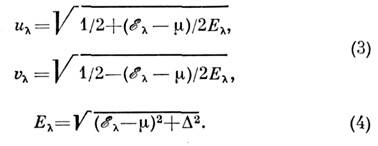
Щель и
и определяется
из ур-ний
определяется
из ур-ний
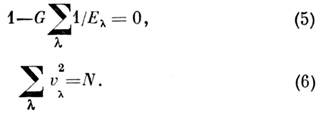
При этом преобразуется в гамильтониан независимых квазичастиц, к-рый (с точностью
до константы) имеет вид:
преобразуется в гамильтониан независимых квазичастиц, к-рый (с точностью
до константы) имеет вид:
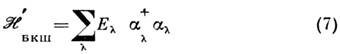
с собств. значениями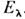 ,
к-рые определяют энергии квазичастичных возбуждений.
,
к-рые определяют энергии квазичастичных возбуждений.
Ур-ние (5) в бесконечной системе имеет решение при сколь угодно слабом
притяжении (G > 0). В конечной системе - ядре это не так; величина
G должна быть порядка расстояния между уровнями энергии нейтронов вблизи
поверхности Ферми (с точностью до численных факторов, возникающих из-за
суммирования по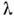 ).
).
Микроскопич. подходы в теории ядра (метод Хартри - Фока - Боголюбова, теория конечных ферми-систем и др.) требуют уточнения соотношений (3) - (6) и точного учёта закона сохранения числа частиц. Однако все качеств. предсказания сверхтекучей модели ядра остаются в силе. Поэтому часто под сверхтекучей модели ядра понимают и более строгие теории, в которых последовательно учитывается нуклонная сверхтекучесть.

Э. Е. Саперштейн
1. Электромагнитная волна (в религиозной терминологии релятивизма - "свет") имеет строго постоянную скорость 300 тыс.км/с, абсурдно не отсчитываемую ни от чего. Реально ЭМ-волны имеют разную скорость в веществе (например, ~200 тыс км/с в стекле и ~3 млн. км/с в поверхностных слоях металлов, разную скорость в эфире (см. статью "Температура эфира и красные смещения"), разную скорость для разных частот (см. статью "О скорости ЭМ-волн")
2. В релятивизме "свет" есть мифическое явление само по себе, а не физическая волна, являющаяся волнением определенной физической среды. Релятивистский "свет" - это волнение ничего в ничем. У него нет среды-носителя колебаний.
3. В релятивизме возможны манипуляции со временем (замедление), поэтому там нарушаются основополагающие для любой науки принцип причинности и принцип строгой логичности. В релятивизме при скорости света время останавливается (поэтому в нем абсурдно говорить о частоте фотона). В релятивизме возможны такие насилия над разумом, как утверждение о взаимном превышении возраста близнецов, движущихся с субсветовой скоростью, и прочие издевательства над логикой, присущие любой религии.
4. В гравитационном релятивизме (ОТО) вопреки наблюдаемым фактам утверждается об угловом отклонении ЭМ-волн в пустом пространстве под действием гравитации. Однако астрономам известно, что свет от затменных двойных звезд не подвержен такому отклонению, а те "подтверждающие теорию Эйнштейна факты", которые якобы наблюдались А. Эддингтоном в 1919 году в отношении Солнца, являются фальсификацией. Подробнее читайте в FAQ по эфирной физике.
|
|