Глоссарий по физике

Размешивание (перемешивание) в фазовом пространстве

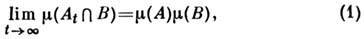
Размешивание (перемешивание) в фазовом пространстве - свойство потока траекторий консервативной динамической системы, достаточное для перехода этой системы в процессе её временной эволюции к стохастич. поведению.

Поток траекторий динамической системы не уходит на бесконечность, и движение происходит в нек-рой ограниченной области D объёмом V_D фазового пространства, тогда формально Р. выражается существованием предела

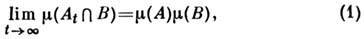
где А, В - две произвольные (как правило, малые) области, принадлежащие D, m(А), m(В)- их меры (B простейшем случае - относит. объёмы этих областей). Обычно область В предполагается фиксированной, а область А эволюционирует во времени в соответствии с Гамильтона уравнениями, A_t - значение А в момент времени t, область A_t 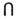В является пересечением областей A_t и В. Для консервативных систем m(A_t) = = m(A) (т. н. инвариантность меры, см. также Лиувил-ля теорема). Р. означает, что независимо от размеров, формы и взаимного расположения областей А а В по прошествии достаточно длительного времени элементы области А могут быть обнаружены в любой сколь угодно малой окрестности произвольной точки области D (рис. 1).

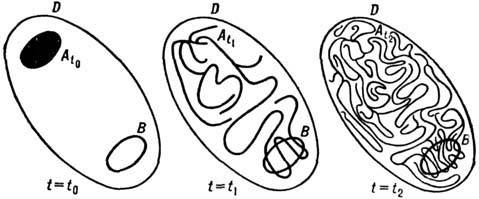
Рис. 1. Эволюция области А в случае размешивания.

Термин "Р." введён Дж. У. Гиббсом (J. W. Gibbs, 1902) по аналогии между движением системы взаимодействующих частиц в фазовом пространстве и перемешиванием жидкостей ("растворителя" и "красителя"). При этом жидкости рассматриваются как непрерывные среды, неразрывные и несжимаемые; реальные молекулярная структура и диффузия не учитываются. Если в нач. момент жидкости не были перемешаны, то при любом возмущении (встряхивание, взбалтывание и др.) такая система с течением времени станет практически однородно перемешанной (рис. 2).

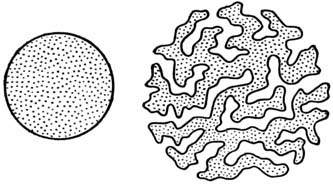
Рис. 2. Расплывание капли при размешивании.

Доказано, что из Р. следует эргодичность системы (см. Эргодическая гипотеза ),однако обратное утверждение неверно. Эргодичность обеспечивает допустимость использования статистических средних лишь в смысле среднего по времени, тогда как при Р. это справедливо и асимптотически. Эргодичность (без Р.) соответствует регулярному квазипериодическому заполнению фазового пространства траекториями, Р.- хаотическому (рис. 3).

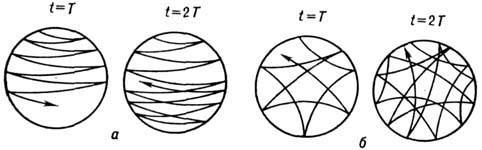
Рис. 3. Различие между эргодическим движением без размешивания (а) и движением с размешиванием (б).

Выполнение условия (1) строго доказано лишь для нек-рых динамич. систем с малым числом степеней свободы. Предполагается, что Р. характерно для мн. систем и отражает общее свойство неустойчивости (раз-бегания) фазовых траекторий по отношению к малым возмущениям нач. условий. Р. обусловливает непредсказуемость и необратимость поведения динамич. системы (хаос динамический). Р. соответствует представлению о характере движений в сложной динамич. системе, требующем перехода к статистич. описанию, но не даёт строгого обоснования применимости методов статистич. механики.

Важнейшим следствием существования Р. является расцепление временных корреляций, т. е. выполнение условия

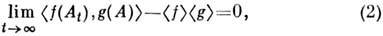
где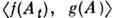- корреляц. функция динамич. переменных f и g, 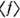и 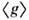- их статистические средние. Свойство (2) означает, что система, обладающая Р., со временем "забывает" о своих нач. условиях и корреляциях.

Литература по размешиванию (перемешиванию) в фазовом пространстве

1. Гиббс Д ж., Термодинамика. Статистическая механика, пер. с англ., М., 1982, гл. 12;
2. Крылов Н. С., Работы по обоснованию статистической физики, М.- Л., 1950;
3. Балеску Р., Равновесная и неравновесная статистическая механика, пер. с англ., т. 2, приложение: Эргодическая проблема, М., 1978;
4. Заславский Г. М., Стохастичность динамических систем, М., 1984, гл. 1;
5. Лоскутов А. Ю., Михайлов А. С., Введение в синергетику, М., 1990.

Д. Н. Зубарев