Простая волна (волна Римана) - волна, каждая точка профиля к-рой распространяется с пост. скоростью и, зависящей от значения
волнового поля y в этой точке. Такие процессы характерны
для нелинейных сред без дисперсии (см. Волны). Одномерная П. в. описывается
выражением
где F - нек-рая функция, определяемая начальным
условием. На плоскости переменных х, t значение y в П. в. сохраняется
на прямых
наз характеристиками. Различным зависимостям
u(y) соответствуют несколько типов П. в. Если
и не зависит от y (линейное приближение),
то П. в. распространяется без изменения формы. В общем же случае профиль П.
в. деформируется.
Пример - движение сжимаемого газа, возбуждаемое
поршнем в трубе. В газе существуют две П. в., распространяющиеся со скоростями
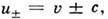где 
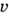скорость частиц, а с - местная скорость звука, зависящая от плотности
в данной точке профиля волны. Если поршень выдвигается из трубы, то в ней возникает
П в разрежения в виде расширяющихся по координате c перепадов
давления, плотности, скорости частиц и т. д. Если же поршень вдвигается в трубу
ускоренно с дозвуковой скоростью, то перед ним распространяется П. в. сжатия,
к-рая непрерывно сокращается вплоть до образования участка с бесконечной крутизной
профиля, что соответствует пересечению характеристик (рис.). В дальнейшем в
волне (1) должна была бы образоваться неоднозначность
- "перехлест" или "опрокидывание" волны сжатия, но в
данном примере это не имеет физ. смысла. На самом деле исходные ур-ния динамики
идеального газа, из к-рых следует решение (1), становятся непригодными в области
резких изменений состояния, и в результате вместо неоднозначности возникает
резкий скачок параметров - ударная волна ,в к-рой существенную роль играют
дис-сипативные процессы (вязкость и теплопроводность среды). Движение за фронтом
ударной волны уже не будет П. в. из-за отражений возмущений от фронта скачка;
лишь при достаточно малой его интенсивности отражения пренебрежимо малы (см.
Нелинейная акустика).
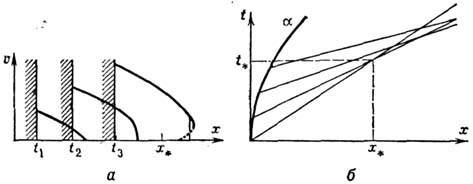
Зволюция скорости частиц в волне, возникающей
при ускоренном вдвигании поршня (а); штриховкой обозначено положение поршня
в последовательные моменты времени. Соответствующий вид (б) характеристики на
плоскости х, t; a, - траектория поршня, x* и t*
- координата и момент образования разрыва.
В П. в. возмущения разл. величин являются функциями
друг друга; эта связь выражается инвариантами Римана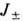 
;
в каждой из П. в. один из инвариантов постоянен. Малые возмущения величин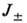
распространяются
в среде только вдоль характеристик (2). В газовой динамике имеются два
инварианта Римана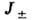 
=
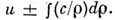В случае идеального политропного газа, характеризуемого показателем политропы g,
Понятие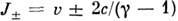
11.
в. применяется и к стационарным двумерным движениям (напр., плоским течениям
газа), тогда в ф-лах (1) и (2) вместо х и t аргументами служат
координаты х и у.
Движение среды вблизи границы с областью пост.
течения (без разрыва на границе) есть П. в.
Аналогичными свойствами обладают П. в. в др.
физ. системах. Однако распространение волны сжатия не всегда приводит к образованию
ударной волны в виде монотонной "ступеньки". В общем случае на участках
большой крутизны профиля вступает в силу не только диссипация, но и дисперсия,
к-рая приводит к появлению осцилляции. Так в эл--магн. системах (плазме, эл--магн.
линиях с ферритом) возникает ударный перепад с осцилляциями, а в отсутствие
потерь - система солитонов .В ряде случаев образование неоднозначности
("перехлёст") имеет реальный физ. смысл. Так, если и - скорость
объектов, движущихся с пост. скоростями без взаимодействия (кинематич. волны),
напр. частиц в разреженном пучке, то "перехлёст" означает просто
обгон одних объектов другими.
Ф-лой (1) может быть описано поведение частоты в частотно-модулированной волне, распространяющейся в среде с дисперсией (тогда и - групповая скорость), или компонент волнового вектора в двумерной геомет-рич. оптике; в последнем случае прямые (1) соответствуют лучам, а их пересечение - образованию каустик или фокусов.
Л. А. Островский
|
|
 |
