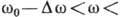
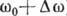 ), тем более узком, чем плавнее и протяжённее огибающая группы. Длина пакета
), тем более узком, чем плавнее и протяжённее огибающая группы. Длина пакета
 и ширина его
спектра
и ширина его
спектра  ограничены
снизу соотношением
ограничены
снизу соотношением 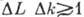 ,
где волновое число k связано с частотой
,
где волновое число k связано с частотой 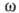 дисперсионным соотношением
дисперсионным соотношением 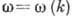 .
.В линейных средах, где соблюдается суперпозиции
принцип, его можно рассматривать как набор гармонич. волн с частотами в
интервале 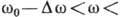
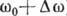 ), тем более узком, чем плавнее и протяжённее огибающая группы. Длина пакета
), тем более узком, чем плавнее и протяжённее огибающая группы. Длина пакета
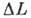 и ширина его
спектра
и ширина его
спектра 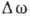 ограничены
снизу соотношением
ограничены
снизу соотношением 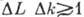 ,
где волновое число k связано с частотой
,
где волновое число k связано с частотой 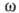 дисперсионным соотношением
дисперсионным соотношением 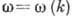 .
.
Если среда не обладает
дисперсией, то все гармонич. волны распространяются с одной и той же фазовой
скоростью, и пакет ведёт себя как строго стационарная волна - его
групповая скорость совпадает с фазовой скоростью 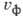 . При наличии дисперсии волны разл. частот распространяются с разными скоростями
и форма огибающей искажается. Однако для сигналов с достаточно узким спектром,
когда фазовые скорости гармонич. волн, образующих волновой пакет, мало отличаются
друг от друга, и на не слишком больших расстояниях, когда форма огибающей приближённо
сохраняется, влияние дисперсии сказывается лишь на скорости перемещения огибающей,
к-рая и есть групповая скорость. Поскольку распространение двух синусоидальных волн с близкими
частотами
. При наличии дисперсии волны разл. частот распространяются с разными скоростями
и форма огибающей искажается. Однако для сигналов с достаточно узким спектром,
когда фазовые скорости гармонич. волн, образующих волновой пакет, мало отличаются
друг от друга, и на не слишком больших расстояниях, когда форма огибающей приближённо
сохраняется, влияние дисперсии сказывается лишь на скорости перемещения огибающей,
к-рая и есть групповая скорость. Поскольку распространение двух синусоидальных волн с близкими
частотами 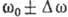 пакета
описывается выражениями
пакета
описывается выражениями
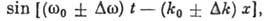
то скорость их огибающей
равна 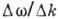 , что в
пределе приводит к ф-ле
, что в
пределе приводит к ф-ле 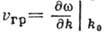 .
На рис. 2 представлены три
последовательных мгновенных снимка сигнала с узким спектром, распространяющегося
в среде с дисперсией. Наклон пунктирных прямых, соединяющих точки одинаковой
фазы (напр., максимумы), характеризует фазовую скорость; наклон прямых, соединяющих
соответствующие точки огибающей (начала и конца сигнала), характеризует
групповую скорость сигнала. Если при распространении сигнала максимумы и минимумы движутся быстрее,
чем огибающая, то это означает, что фазовая скорость данной группы волн превышает
её групповую скорость. (рис. 2, а). При распространении сигнала в его "хвостовой"
части возникают всё новые максимумы, к-рые постепенно перемещаются вперёд, достигают
его головной части и там исчезают. Такое положение имеет место в случае т. н.
нормальной дисперсии, т. е. в средах, где показатель преломления
.
На рис. 2 представлены три
последовательных мгновенных снимка сигнала с узким спектром, распространяющегося
в среде с дисперсией. Наклон пунктирных прямых, соединяющих точки одинаковой
фазы (напр., максимумы), характеризует фазовую скорость; наклон прямых, соединяющих
соответствующие точки огибающей (начала и конца сигнала), характеризует
групповую скорость сигнала. Если при распространении сигнала максимумы и минимумы движутся быстрее,
чем огибающая, то это означает, что фазовая скорость данной группы волн превышает
её групповую скорость. (рис. 2, а). При распространении сигнала в его "хвостовой"
части возникают всё новые максимумы, к-рые постепенно перемещаются вперёд, достигают
его головной части и там исчезают. Такое положение имеет место в случае т. н.
нормальной дисперсии, т. е. в средах, где показатель преломления 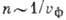 увеличивается с ростом частоты гармонич. волны
увеличивается с ростом частоты гармонич. волны  .
Такую дисперсию наз. также отрицательной, поскольку с ростом k фазовая
скорость волны убывает. Примеры сред с нормальной дисперсией - вещества, прозрачные
для оптич. волн, волноводы, изотропная плазма и др. Однако в ряде случаев наблюдается
аномальная (положительная) дисперсия среды
.
Такую дисперсию наз. также отрицательной, поскольку с ростом k фазовая
скорость волны убывает. Примеры сред с нормальной дисперсией - вещества, прозрачные
для оптич. волн, волноводы, изотропная плазма и др. Однако в ряде случаев наблюдается
аномальная (положительная) дисперсия среды  ;
в этих случаях групповая скорость сигнала превышает его фазовую скорость
;
в этих случаях групповая скорость сигнала превышает его фазовую скорость 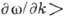
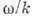 .
Максимумы и минимумы появляются в передней части сигнала (рис. 2, б), перемещаются
назад и исчезают в его хвосте. Аномальная дисперсия характерна для капиллярных
волн на поверхности воды (
.
Максимумы и минимумы появляются в передней части сигнала (рис. 2, б), перемещаются
назад и исчезают в его хвосте. Аномальная дисперсия характерна для капиллярных
волн на поверхности воды (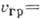
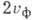 ),
для эл--магн. и акустич. волн в средах с резонансным поглощением, а также при
определ. условиях - для волн в периодич. структурах (кристаллы, замедляющие
системы и т. п.). При этом возможна даже ситуация, при к-рой
групповая скорость направлена
противоположно фазовой. Волны, обладающие этим свойством, наз. обратными.
),
для эл--магн. и акустич. волн в средах с резонансным поглощением, а также при
определ. условиях - для волн в периодич. структурах (кристаллы, замедляющие
системы и т. п.). При этом возможна даже ситуация, при к-рой
групповая скорость направлена
противоположно фазовой. Волны, обладающие этим свойством, наз. обратными.
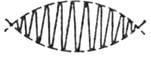
Рис. 1. Волновой пакет.
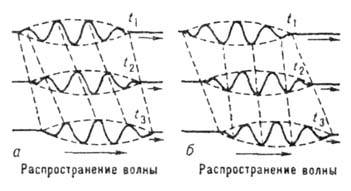
Рис. 2. Последовательные
моментальные снимки группы волн в моменты времени t1, t2,
t3 в случае нормальной дисперсии (a) и в случае
аномальной дисперсии (б).
Групповая скорость определяет скорость и направление переноса энергии волнами. В анизотропных средах (напр., кристаллах,
плазме в пост. магн. поле), где показатели преломления волн зависят от частоты
и направления распространения, групповая скорость определяется как векторная производная
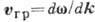 и обычно не совпадает
по направлению с фазовой скоростью. В средах с сильным поглощением вместо
групповой скорости вводят величину, характеризующую скорость переноса энергии
и обычно не совпадает
по направлению с фазовой скоростью. В средах с сильным поглощением вместо
групповой скорости вводят величину, характеризующую скорость переноса энергии 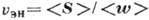 ,
где
,
где 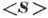 - ср. плотность
потока энергии, а
- ср. плотность
потока энергии, а 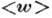 - ср. плотность энергии в волнах. В прозрачных средах величины
- ср. плотность энергии в волнах. В прозрачных средах величины 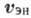 и
и 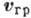 совпадают.
совпадают.
Понятие групповой скорости играет важную роль и в физике, и в технике, поскольку все методы измерения скоростей распространения волн, связанные с запаздыванием сигналов (в т. ч. скорости оптического излучения), дают групповую скорость. Она фигурирует при измерении дальности в гидро- и радиолокации, при зондировании ионосферы, в системах управления космич. объектами и т. д.

M. А. Миллер, E. В. Суворов
|
|