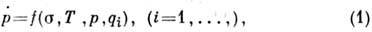 ур-ние
состояния в виде где r - деформация
ползучести,
ур-ние
состояния в виде где r - деформация
ползучести, 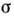 -
напряжение, Т - темп-pa,
-
напряжение, Т - темп-pa, 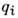 -
т. н. параметры состояния, для к-рых записывается система кинетич. ур-ний вида
-
т. н. параметры состояния, для к-рых записывается система кинетич. ур-ний видаМатематическая теория ползучести - раздел механики сплошных сред, в к-ром изучают процессы медленного деформирования
(течения) твёрдых тел под действием пост, напряжения (или нагрузки). В силу
различия физ. механизмов, приводящих к возникновению временных эффектов, единой
П. т. не существует. Наиб, развитие получили варианты П. т., описывающие поведение
наиб, распространённых конст-рукц. материалов: металлов, пластмасс, композитов,
грунтов, бетона. Осн. задача П. т.- формулировка таких матем. зависимостей между
деформацией ползучести (или её скоростью) и параметрами, характеризующими состояние
материала (механич. напряжения, темп-pa, повреждённость и др.), к-рые бы достаточно
полно отражали осн. наблюдаемые в экспериментах свойства. К П. т. непосредственно
примыкают теории т. н. длит. прочности, описывающие разрушение материалов при
выдержке в условиях постоянной или слабо меняющейся нагрузки.
Механич. характеристики ползучести и длит. прочности
конструкц. материалов обычно определяют в опытах на растяжение или сжатие цилиндрич.
образцов (одноосное напряжённое состояние) либо путём испытаний трубчатых или
плоских образцов при разд. комбинациях нагрузок (сложное напряжённое состояние).
Длительность испытаний зависит как от уровня нагрузок, так и от задач использования
данного материала в конкретных конструкциях. Она может колебаться от неск. минут
(для решения технол. задач обработки металлов, непрерывной разливки, ракетной
техники) до сотен тысяч часов (стационарные турбины, строит. конструкции).
Наиб. распространение получили два подхода к
построению П. т. В первом в качестве осн. соотношения принимается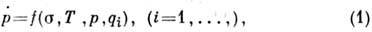 ур-ние
состояния в виде где r - деформация
ползучести,
ур-ние
состояния в виде где r - деформация
ползучести, 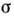 -
напряжение, Т - темп-pa,
-
напряжение, Т - темп-pa, 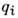 -
т. н. параметры состояния, для к-рых записывается система кинетич. ур-ний вида
-
т. н. параметры состояния, для к-рых записывается система кинетич. ур-ний вида
 где коэф.
где коэф. 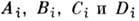 сами
могут быть функциями
сами
могут быть функциями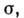
 Задавая конкретные виды функций
Задавая конкретные виды функций и
и 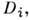 можно получить все известные, т. н. техн. П. т. Так, если принять, что параметр
можно получить все известные, т. н. техн. П. т. Так, если принять, что параметр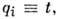 получим
теорию течения, а если ограничиться одним ур-нием (1), то теорию упрочнения.
Вводя параметр повреждённости w (под к-рым понимается обобщённая мера микротрещин),
получим соотношения вида
получим
теорию течения, а если ограничиться одним ур-нием (1), то теорию упрочнения.
Вводя параметр повреждённости w (под к-рым понимается обобщённая мера микротрещин),
получим соотношения вида
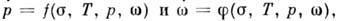 к-рые позволяют описать как процесс ползучести, так и длит. разрушение (обычно
для сплошного, неповреждённого материала принимается
к-рые позволяют описать как процесс ползучести, так и длит. разрушение (обычно
для сплошного, неповреждённого материала принимается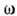 =
0, а условие разрушения - в виде
=
0, а условие разрушения - в виде 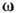 = 1). Введение двух параметров повреждённости
= 1). Введение двух параметров повреждённости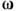 и
и 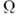 позволяет
описать наиб. характерные эффекты длит. прочности. Соотношения (1) и (2) позволяют
учесть все осн. участки кривых простой ползучести (когда испытания
проводятся при пост. напряжении). Кроме того, в них могут быть учтены и такие
эффекты, как скачкообразное изменение скорости ползучести при мгновенных догрузках
и разгрузках и эффект последействия. Во втором подходе принимается зависимость
вида
позволяет
описать наиб. характерные эффекты длит. прочности. Соотношения (1) и (2) позволяют
учесть все осн. участки кривых простой ползучести (когда испытания
проводятся при пост. напряжении). Кроме того, в них могут быть учтены и такие
эффекты, как скачкообразное изменение скорости ползучести при мгновенных догрузках
и разгрузках и эффект последействия. Во втором подходе принимается зависимость
вида 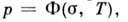 где
под F понимается нек-рый функционал по времени г. В частном случае, когда
он может быть записан в виде
где
под F понимается нек-рый функционал по времени г. В частном случае, когда
он может быть записан в виде
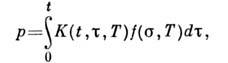
получаем обычную теорию наследственности. Величина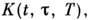 т.
н. ядро последействия, характеризует, насколько в момент времени t ощущается
влияние (последействие) на деформацию напряжения, к-рое действовало в более
ранний момент времени
т.
н. ядро последействия, характеризует, насколько в момент времени t ощущается
влияние (последействие) на деформацию напряжения, к-рое действовало в более
ранний момент времени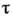 Т. к. напряжение действует и в др. моменты времени, то суммарное последействие
учитывается интегрированием. Если ядро К зависит только от разности
Т. к. напряжение действует и в др. моменты времени, то суммарное последействие
учитывается интегрированием. Если ядро К зависит только от разности то
имеем дело с нестареющим материалом, а если
то
имеем дело с нестареющим материалом, а если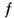 является
линейной функцией
является
линейной функцией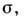 то
получается линейная теория наследственности. Когда К является экспоненциальной
функцией от
то
получается линейная теория наследственности. Когда К является экспоненциальной
функцией от получаем
известные модели вязкоупругих сред. В более общем случае F может быть представлено
в виде ряда кратных интегралов по времени. Тогда получаем соотношения общей
нелинейной теории вязкоупругости.
получаем
известные модели вязкоупругих сред. В более общем случае F может быть представлено
в виде ряда кратных интегралов по времени. Тогда получаем соотношения общей
нелинейной теории вязкоупругости.
Переход к сложному напряжённому состоянию осуществляется
обычно принятием одной из двух гипотез для деформаций ползучести: в первом случае
принимается, что тензор деформаций ползучести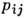 пропорционален
девиатору тензора напряжений
пропорционален
девиатору тензора напряжений 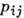 =
=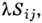 во втором принимается гипотеза о пропорциональности тензора скоростей деформаций
ползучести
во втором принимается гипотеза о пропорциональности тензора скоростей деформаций
ползучести 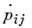 тому
же девиатору
тому
же девиатору  Первая - деформац. вариант, вторая - теория течения для сложного напряжённого
состояния. Параметр
Первая - деформац. вариант, вторая - теория течения для сложного напряжённого
состояния. Параметр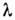 определяется
как отношение соответствующих инвариантов тензоров деформаций ползучести и напряжений,
для определения к-рых принимаются системы (1) и (2), куда в качестве параметров
могут войти произвольные инварианты тензоров напряжений и деформаций.
определяется
как отношение соответствующих инвариантов тензоров деформаций ползучести и напряжений,
для определения к-рых принимаются системы (1) и (2), куда в качестве параметров
могут войти произвольные инварианты тензоров напряжений и деформаций.
Математическая теория ползучести используется для анализа напряжённо-деформированного состояния и времени работоспособности элементов конструкций, материал к-рых обладает свойствами ползучести и длит. прочности. Соотношения (1), (2) дополняют систему ур-ний равновесия и совместности до полной. В условиях ползучести при пост. внеш. воздействиях может со временем произойти потеря несущей способности отд. элементов конструкций и конструкции в целом. Это относится, в частности, к потере устойчивости элементов типа арок и оболочек, где возможна потеря устойчивости при нагрузках, существенно меньших, чем вызывающие мгновенную потерю устойчивости при нагружении. Важное значение имеют расчёты длит. прочности, когда возможно наступление мгновенного разрушения при длит. эксплуатации в условиях стационарного режима нагру-жения. П. т. позволяет найти оптим. режимы ряда технол. процессов высокотемпературной обработки металлов, изготовления композитных материалов и оценить временные процессы при деформации грунтов, ледников и др. природных сред.

С. А. Шестериков
Релятивисты и позитивисты утверждают, что "мысленный эксперимент" весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: "Если факт не соответствует теории - измените факт" (В другом варианте " - Факт не соответствует теории? - Тем хуже для факта").
Максимально, на что может претендовать "мысленный эксперимент" - это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
Понятие "мысленный эксперимент" придумано специально спекулянтами - релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим "честным словом". Подробнее читайте в FAQ по эфирной физике.
|
|